十分钟了解Kubernetes

何为Kubernetes?

最简单的一句话来概括Kubernetes。它就是一套成熟的商用服务编排解决方案。Kubernetes定位在Paas层，重点解决了微服务大规模部署时的服务编排问题。

Kubernetes组件介绍

了解Kubernetes都是从Pod开始的。Pod是Kubernetes最小的调度单元，所以组件介绍就从Pod开始。Pod是一组容器的集合，这些容器共享IPC，Network和UTS，也就是这些容器相互之间可以共享进程信息，网络信息和主机信息。这一组容器相互之间可以通过Localhost互访。

640?wx_fmt=jpeg

Kubernetes其它组件都是围绕着Pod来工作的。

Pod有时也称为实例(或者服务实例)。当我们说一个服务存在2个实例时，也就是说这个服务有两个Pod。

在Kubernetes中可以单独创建Pod，单独管理Pod。但这却无法体现出服务编排的优势，例如需要资源利用率动态伸缩，或者对外部提供网络访问。这时Kubernetes就又提供了一些管理Pod的组件。这些组件适用于不同的场景，但本质都是在管理Pod。

以下先介绍DaemonSet、ReplicaSet、StatefulSet和Job这四个组件。

DaemonSet用来保证在集群中每个计算节点中都运行指定的Pod。这个组件通常用来运行监控类和数据采集类的Pod，像定时采集节点资源信息，采集节点容器日志等等。

ReplicaSet，有时简称RS。和它相对应的有RC(新版本中已经剔除了)。此组件用来维护Pod状态，时刻让集群中Pod的状态满足用户所期望的状态。例如用户期望运行4组Pod，当集群中Pod数量大于4或者小于4时，都会动态缩容或扩容来满足4组Pod这样的状态。

StatefulSet，专为解决有状态应用而推出的组件。DaemonSet和ReplicaSet都是无状态的，也就是Pod的启停和网络信息都是无序的。而StatefulSet则会保证Pod的启停顺序和网络信息与之前是保持一致的。

Job，顾名思义，是运行作业的组件。使用Job组件会保证Pod至少执行成功一次。
添加这四个组件之后，上面的图就变成了下面的样子: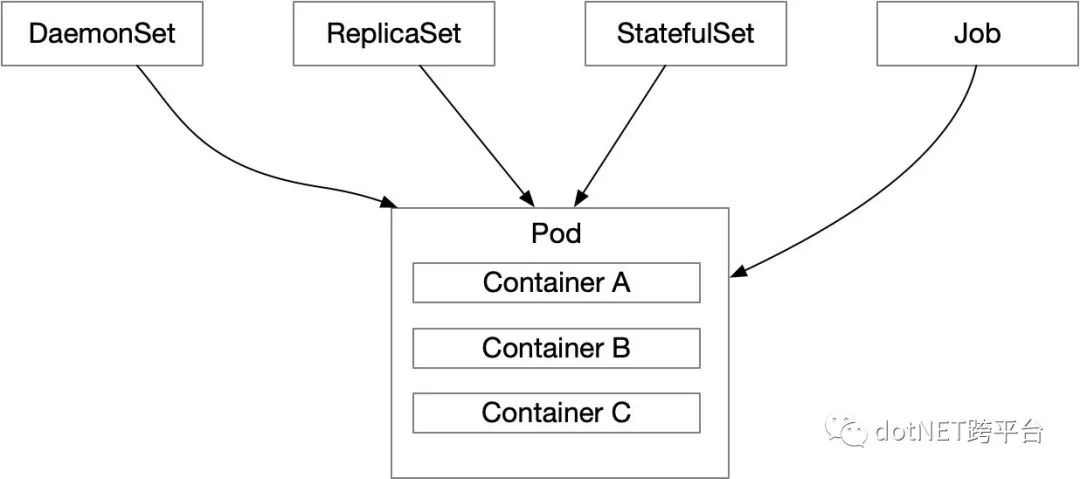
640?wx_fmt=jpeg

在上面四个组件里面，ReplicaSet是使用最多的组件，90%的Pod的创建、销毁都是通过RS来完成的。但RS在使用上还是有点不方便，例如Pod p1现在要修改Container A的镜像版本。那么就需要在创建一份新RS，然后通过新RS来创建新的Pod p2。等p2创建完成之后，在返回来销毁p1。这个时候就会同时存在RS1和RS2，当变更很频繁时，RS的管理就会变成瓶颈。所以Kubernetes增加了Deployment来管理ReplicaSet，请注意Deployment是直接管理ReplicaSet的，而ReplicaSet则直接管理Pod。所以Deployment是间接管理Pod。

通过Deployment，用户可以声明最新的Pod状态，例如新镜像版本，新的环境变量，新的数量等等这些状态信息。Deployment会通过动态创建和销毁ReplicaSet来满足用户所期望的状态，用户不需要关心中间过程如何实现(声明式API就是好)。

因此上面的图就变成了下面的样子: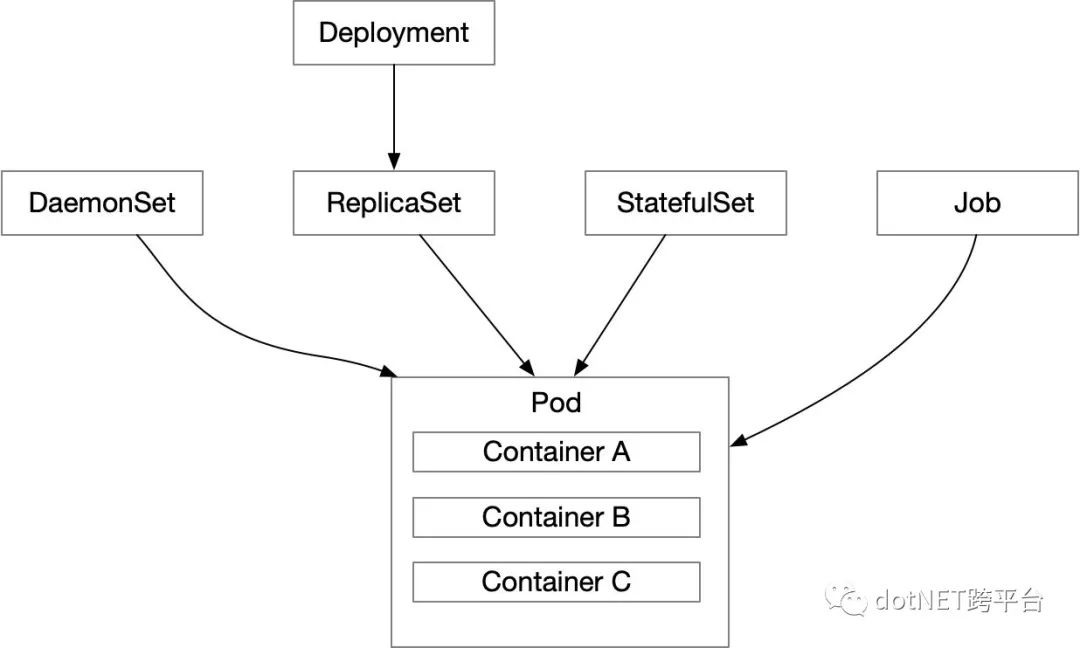
640?wx_fmt=jpeg

和Deployment类似，Kubernetes也提供了CronJob来动态管理Job，其实就是定时作业。因此就不多说了。在上图中再添加一个CronJob。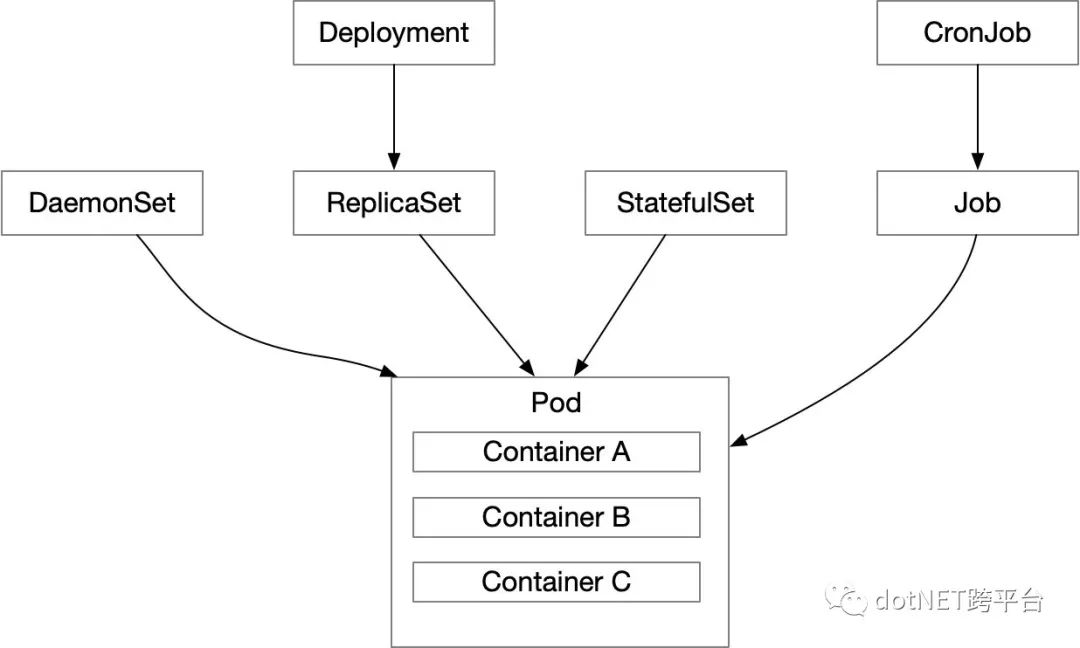
640?wx_fmt=jpeg

说到现在，管理Pod基本就聊完了。此时创建的Pod会有以下特点：

每个Pod都是内网IP。
Pod销毁/创建会产生新IP。

那么如何访问这些Pod呢？访问分两类，集群内访问和集群外访问。但无论是集群内访问还是集群外访问，Pod的变更都不应该对调用方产生干扰。因此对于调用方来说Pod的IP必须要固定下来。而Service就应运而生，用来解决这个问题。

Kubernetes可以为一组Pod创建一个单独的Service，这个Service拥有固定的IP，并会将网络请求转发到相对应的这组Pod上。通俗来说，Service就是4层LB。好吧，上面的图在添加点东西：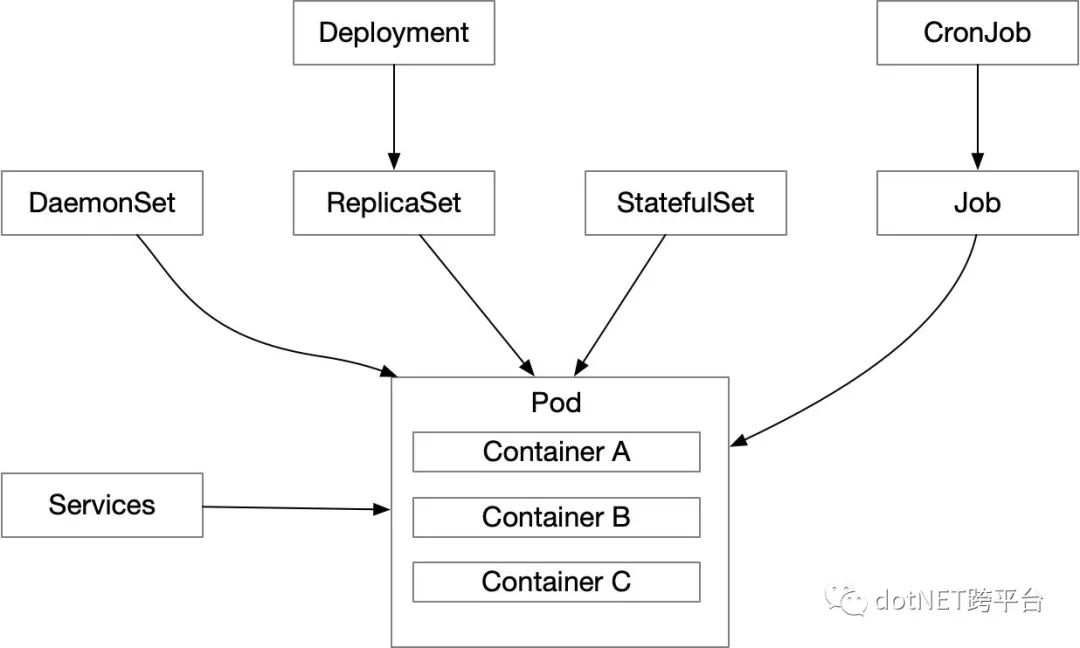
640?wx_fmt=jpeg

Service产生的基本都是内网IP(也可以产生其它网段IP，但不在极简史讨论范畴)，并且是4层LB。如果要对集群外开放网络请求，就需要使用Kubernetes提供的Ingress组件。

Ingress是7层LB，而使用最多的是Nginx Ingress。这个时候再添加点东西：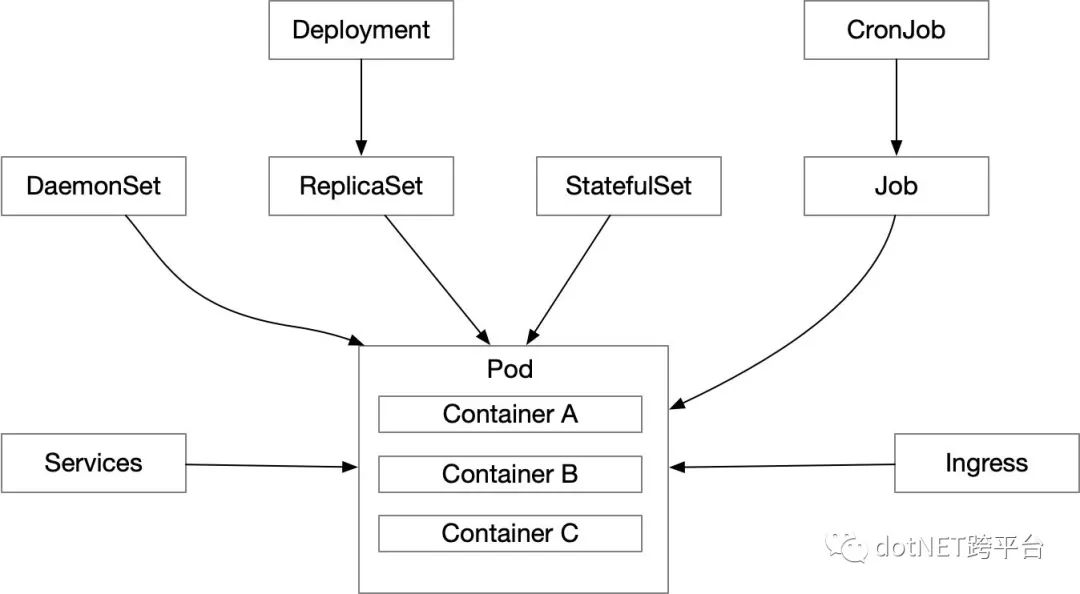
640?wx_fmt=jpeg

从大面上说，几个大组件都齐了。下面再说Pod持久化和参数配置的问题。

Pod持久化就需要挂载Volume，通过将数据写入指定Volume的方式来完成持久化。Kubernetes为Volume提供了多种实现方式，大体分为两类：临时挂载和永久挂载。第三次请注意：
临时挂载指的是卷随着Pod的生命周期而存在，当Pod被删除时挂载的Volume也会随之消失。而永久挂载则是真的永久保存。

临时挂载有EmptyDir和HostPath两种方式。永久挂载称之为PresistentVolume(PV)。PV是与Pod完全无关的一种资源，当Pod有持久化需求时，就需要向PV申请所需要的资源，这种资源称之为PersistentVolumeClaim(PVC)。

简单理解，PV就是存储池，PVC就是向存储池中申请存储资源。
在Pod中添加所申请的PVC，Pod产生的数据就可以写入到存储池中了。上面的图再增加点东西: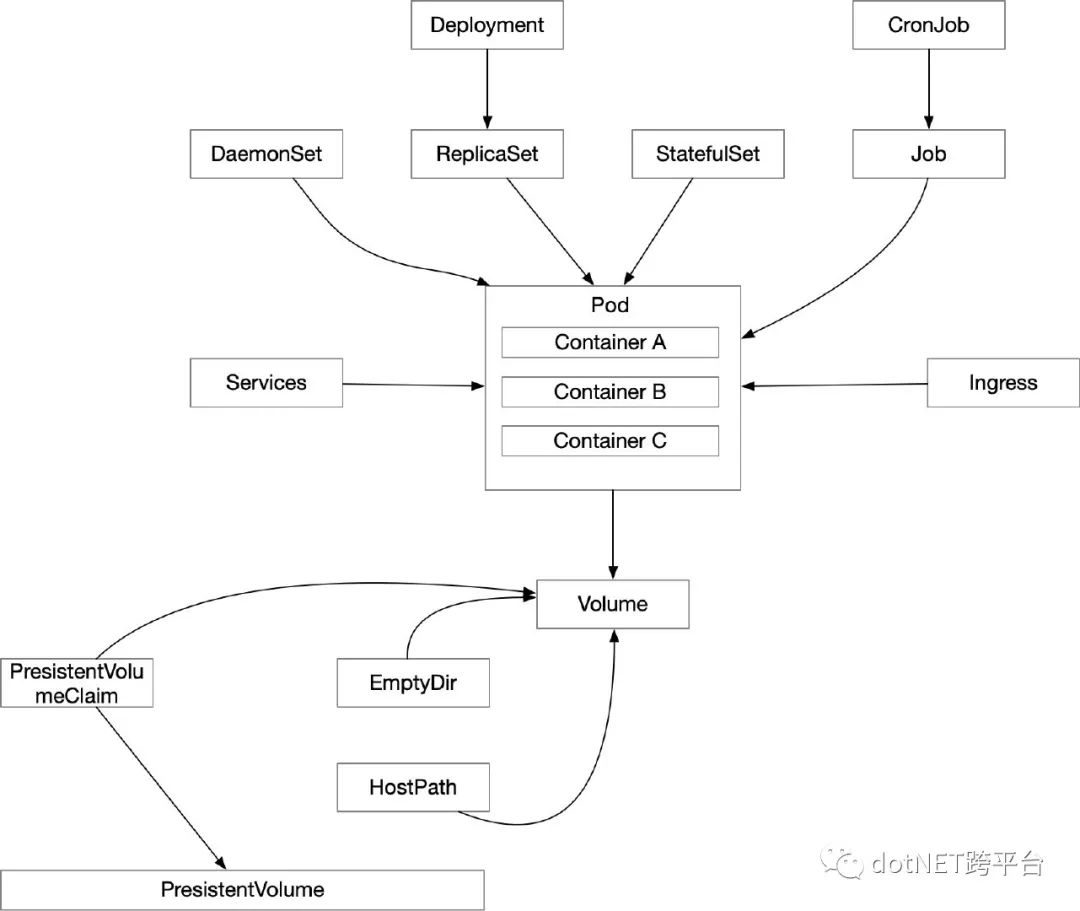
640?wx_fmt=jpeg

极简史就剩下最后一部分了：配置文件。
配置文件指的是Kubernetes支持Pod创建时，将指定的配置文件以文件或者环境变量的形式添加到Pod中。在Kubernetes中这类配置文件称之为configmap。既然是配置文件，就免不了会涉及到口令，放入配置文件就很不安全。Kubernetes为这类需求单独提供了secret，其实就是特殊的configmap。为啥是特殊，其实就是将口令做了Base64编码，连加密都不是。。
所以最后这张图就变成了这样：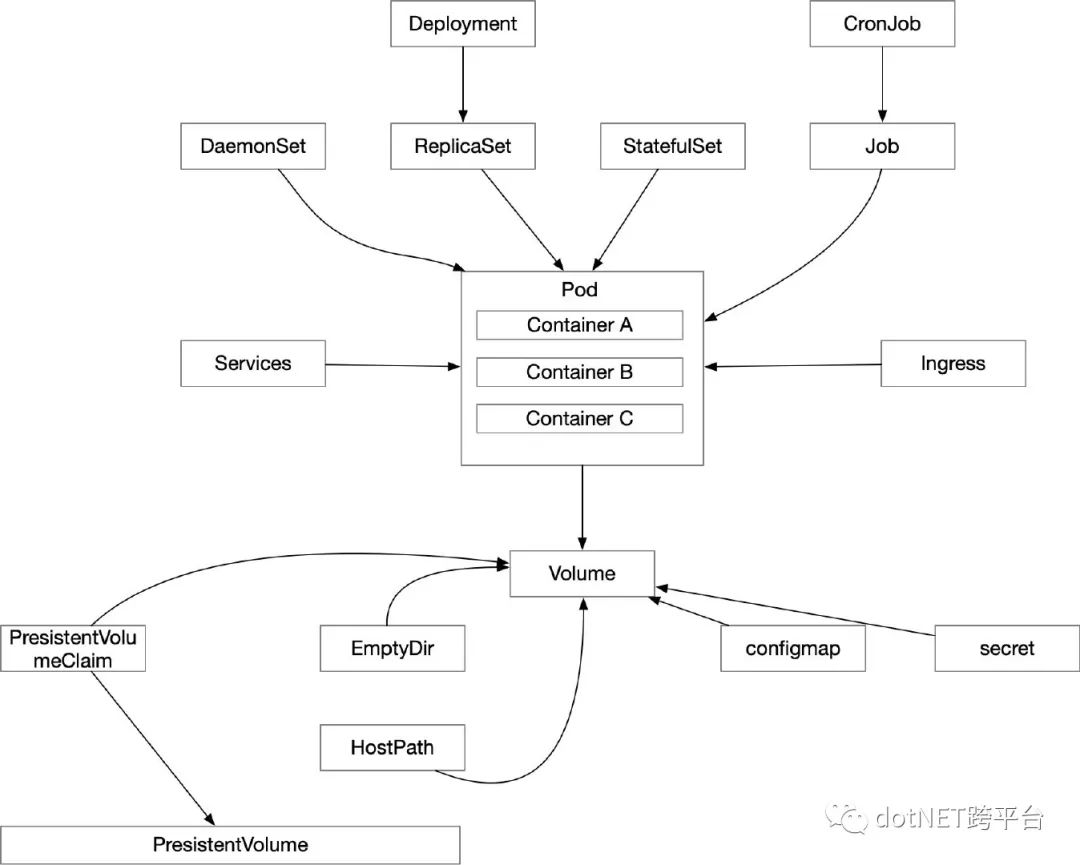
640?wx_fmt=jpeg