前言

微服务从大规模使用到现在已经有很多年了，从之前的探索到一步步的不断完善与成熟，微服务已经成为众多架构选择中所必须面对的一个选项。服务注册与发现是相辅相成的，所以一般会合起来思索。其依托组件有很多，比如Zookeeper,Consul，Eureka等等。

本文，我们将探讨服务注册和发现的概念及其使用机制，以使得微服务能够在不知道其确切位置（通常是URL）的情况下消费其他服务。由于本文主要是个人实践的一些总结，总会有不足之处，也希望各位看官帮忙完善。本系列前一篇文章请移步总述

服务注册与发现探讨

为什么需要

服务是在具有单独部署周期的不同计算机上运行的单个或较小的代码库，可明确解决相关的问题域。不正确的服务设计可能导致重复的服务创建，同时也无法进行架构层面的复用。

如果没有服务注册与服务发现，那么服务的位置将会耦合到消费者服务里面，最终将会导致整个系统的架构变得死板而又难以维护。事实上，在比较简单的系统架构里，采用静态配置的方式是非常简单而又效果显著的，毕竟所有服务都在同一位置，而且很少发生变更。

而在微服务里，其目标之一就是使系统能够独立开发、部署及升级扩展，随着系统的进一步复杂，服务位置也发生变更，那么静态配置就会变得十分鸡肋，此时我们需要变更我们的策略，那就是在消费其他服务的时候采用静态配置。那么核心问题就来了，服务是如何发现它们索要消费的服务的IP地址和端口号的？既是动态配置，在多实例场景下，配置在专门的系统里是最好的选择，ZK和Consul等也就应运而生。

简单的通信流程

我们来看一下一个简单的服务通信流程

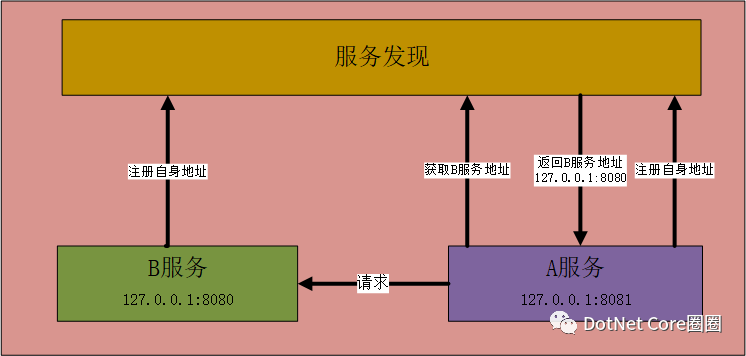
透过这张图，我们可以知道，服务调用时，无需知道目标服务的真实地址，只需要知道服务Key，然后到服务发现系统里获取对应的地址即可。

这张图虽然比较简单，但是传递的信息却有很多：

服务如何确定自身的IP地址及端口？

在消费方拿到被消费方的地址以后，应采用何种方式调用？

我们如何添加新服务并删除已弃用的服务？

如果服务在运行过程中出现问题，如何快速发现并提前通知？

作为集中化管理的服务注册与发现中心挂了，咋整？

服务信息注册

一般可以创建服务注册表，该服务注册表是服务及其实例及其位置的数据库。服务实例在启动时注册到服务注册表，并在关闭时注销。客户端查询服务注册表以查找服务的可用实例。服务注册表可能会调用服务实例的运行状况检查API来验证它是否能够处理请求。我们已经有了现成的工具，就是Consul等，那么我们的关注点就是服务地址的注册了。

最简单的解决方案就是手动配置。我们思考一个问题，如果我们需要对该服务进行水平扩展，再增加一个实例的时候，仍然需要我们手动配置，但是我们已经不想手动配置了，在DevOps时代，再使用手动配置，就显得不那么专业了，而且人工的介入，也增加了系统运维的成本与风险。

所以我们选择，自动获取本机IP地址，但是这里有一个问题，也是我在实际运用中遇到的问题就是本地会有多个网卡的情况，这是比较麻烦的，所以那时候我建议每台机器只配置一个网卡，以减少不确定性，但是后来，遇到一个新的问题就是，当我想在服务器上安装代理，以获取请求包信息的时候，容易改变系统的运行环境，依然存在着不确定性。后来我在网上查看是否其他方案的时候，始终没有一个比较好的解决方案，后来有人说，直接往服务注册中心发送一个Socket连接就可以了，通过Socket实例获取本机IP，网上也有人介绍这种方案。

至于端口获取，相对简单一点，我们使用的就是直接配置在服务里。

服务注册本身就是要在有限人力干预的情况下，支持不同应用之间的运行与交互。

服务注册扩展至之其他信息的注册

这个地方更多的是考虑服务消费方的负载均衡策略、调用策略以及容错的可配置性。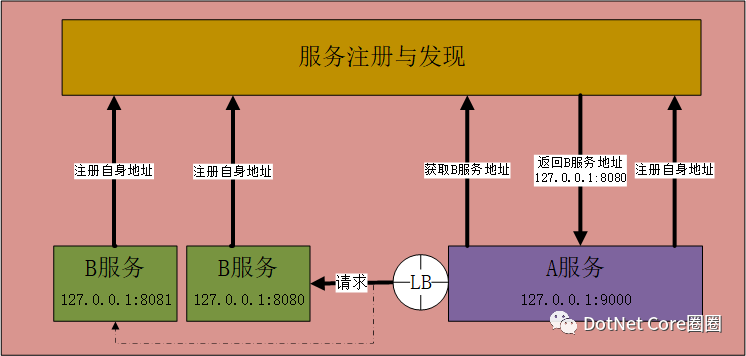

在被消费方做了集群部署的时候，这就是要求我们根据实际运行情况及时调整对服务的调用，那么该如何判断呢？在实现上可以考虑权重参数，该参数的设置应该来源于自身以及服务治理系统。

来源于自身，是因为我们的服务可能部署在相对较差的机器上或者该服务本身只是一个备用系统，不应该承载过大的流量。

来源于服务治理系统，是因为在实际运行中，可能该系统已经出现问题，或者需要暂时下线，我们可以设置权重系数为0，以从消费服务本身来停止对该服务的调用。

权重参数只是其中一个，也是最容易想到和实现的一个，当然还有其他参数，只要是为了更好的优化服务间的调用，那么就可以注册进去，同时实现相应的调用策略。比如版本号，TTL等等。

一旦信息多了，就需要考虑如何及时获取变更，以调整调用策略。

服务发现

服务发现可以分为客户端发现或服务器端发现来确定要向其发送请求的服务实例的位置。客户端发现比较简单一些，直接向服务发现中心获取所需的被消费者服务的信息。而服务端发现相对来说，比较复杂，需要创建一个路由中心，由路由中心去发现被消费者的请求。我们这边用的比较多的是客户端发现。

确保发现的稳定性，首先就要确保服务注册中心的稳定性，其地址不应该频繁发生变化，所以我们可以在服务中配置我们的服务注册中的地址。此处需要多说明一下，就是作为服务注册中心系统，一定要保持高可用性，可以通过集群以及负载均衡来增强可用性。

服务实例的数量及其位置是动态变化的。通常为虚拟机和容器分配动态IP地址。最复杂的问题自然是如何及时获得被消费者服务变化后的地址？我们可以创建一个路由功能，用户可以客户端查询服务注册中心以查找服务的可用实例。服务注册中心可能会调用服务实例的运行状况检查API来验证它是否能够处理请求。

我们在系统启动的时候，会做个Reload，以加载最新信息。那么之后如何及时获取最新信息呢？通常情况下有两种，主动轮询和获取推送消息。

主动轮询带有随机性，如果恰恰好，可能会很及时，大多数情况下，可能没那么恰恰好，而且还要增加服务发现中心的负载压力。

推送方式在效果上可能更好一些，在具体实现上可能没有那么简单。

健康检查

一般而言，健康检查包括，客户端心跳和服务端主动探测两种方式，

首先来说，客户端心跳，就是客户端通过TCP或者HTTP的方式，告诉服务端自身的运行情况，当然客户端通知是有弊端的，比如客户端在某一时间点出现故障时，无法及时通知服务端，事后恢复运行后，告知的也只是当前的运行状态，即便这时再告诉服务端之前的运行状况，也对服务调用没有什么太大意义了，只是对服务本身的运行分析起到了一定作用。即便是保持正常连接的情况下，服务也未必是可以调用的，比如数据库挂掉。

一般而言，采用服务端探测的比较多一些，调用方式和客户端心跳差不多，但是仍然需要我们注意的是，客户端所提供的探测接口必须具有通用性，比如可以查一下次数据库等等，这样可以比较全面的反应系统的运行情况。

容灾与故障转移

容灾的原因有很多，比如服务不再使用、双11大流量的涌进，使得其中一些服务不可用，也就不得不针对性的对一些服务进行容灾处理，以集中资源给核心应用。在容灾过程中，可以给服务下线功能可以制定一些策略，以丰富功能的使用。.NET Core里面可以使用IApplicationLifetime来显示下线功能。当然也需要提供手动下线的接口。

容灾主要考虑方向是客户端容灾和服务端容灾。客户端容灾中，如果服务注册中心挂掉了，恢复运行可能需要一段时间，在这个过程中如果保证服务正常运行。在实际运行中非常有可能发生这种情况，我们可以将服务发现中心获取的信息缓存起来，缓存方式有很多，无外乎是本地内存、文件以及外部存储，本地内存还要还要考虑该服务重启过程中的数据丢失，所以可选的方式就有内存+文件方式。反之，为了达到容灾的要求，我们可以在获取服务发现中心返回的数据的过程中将数据存在到内存和文件中，可以采用异步方式存储。

如下图所示，在发现过程中，使用缓存功能，如果缓存都失效了，那就真的要game over一阵子了。

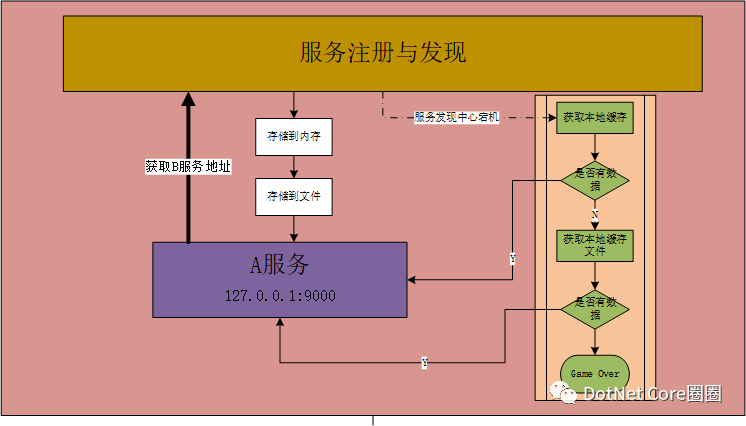
服务端容灾，就比较简单了，因为现在大多数做的都是服务端容灾，比如集群等水平扩展方式， 可主动从其他节点同步相应的数据，也可等待master的同步。

总结

服务注册与发现在服务生命周期中发挥着重要作用。动态的服务注册和发现变得非常重要，它可以避免服务中断。在处理服务实例的容灾与故障转移时，尽量实现自动转移，并提供手动方式处理，而对于跨服务调用，尤其是该服务拥有多实例服务的时候，需要考虑负载平衡。