如果你使用过一些开源CMS的话，肯定会用过其中的的插件化功能，用户可以通过启用或者上传插件包的方式动态添加一些功能，那么在ASP.NET Core MVC中如何实现插件化开发呢，下面我们来探究一下。

本系列只是笔者的一些尝试，并不表示一定正确，只是为了分享一些思路，大家可以一起讨论一下，后续会不断更新。

在ASP.NET Core中进行插件话开发，就不得不说ApplicationPart。 ApplicationPart是ASP.NET Core一个重要组件，它是应用程序资源的一种抽象，通过它可以发现程序集中包含的控制器、视图组件、TagHelper和预编译Razor视图等MVC功能。

默认情况下，当一个ASP.NET Core MVC应用启动时，它只会尝试在当前应用启动的项目及引用的项目中加载控制器，如果想从未直接引用的程序集中加载控制器和预编译Razor视图，我们就需要借助ApplicationPart了。

而ASP.NET Core MVC中，有一个ApplicaitonPartManager类, 通过ApplicationPartManager我们可以来配置当前应用中使用哪一些ApplicationPart。

例：

var assembly = Assembly.LoadFile("demo.dll");var assemblyPart = new AssemblyPart(assembly);var mvcBuilders = services.AddMvc();mvcBuilders.ConfigureApplicationPartManager(apm =>{    apm.ApplicationParts.Add(assemblyPart);});

下面呢，我们通过一个最简单的实例，给大家演示一下如何借助ApplicationPart，动态加载第三方程序集中的控制器和预编译视图。

首先我们创建一个ASP.NET Core MVC的站点，命名为DynamicPluginsDemoSite

然后我们同时创建一个.NET Core Class Library项目，命名为DemoPlugin1, 同时对该项目引用

• Microsoft.AspNetCore.App

• Microsoft.AspNetCore.Razor

• Microsoft.AspNetCore.Razor.Design

注意：针对以上3个程序集，需要保证DynamicPluginsDemoSite和DemoPluigin1使用的相同的版本。

这里为了保证Razor视图的预编译，我们需要打开DemoPlugin1项目的工程文件DemoPlugin1.csproj。将项目使用的SDK从"Microsoft.NET.Sdk"改为"Microsoft.Net.Sdk.Razor"。

<Project Sdk="Microsoft.NET.Sdk.Razor">  <PropertyGroup>    <TargetFramework>netcoreapp2.2</TargetFramework>  </PropertyGroup>  <PropertyGroup Condition="'$(Configuration)|$(Platform)'=='Debug|AnyCPU'">    <OutputPath>C:\Users\Lamond Lu\source\repos\DynamicPlugins\DynamicPluginsDemoSite\bin\Debug</OutputPath>  </PropertyGroup>  <ItemGroup>    <PackageReference Include="Microsoft.AspNetCore.App" Version="2.2.0" />    <PackageReference Include="Microsoft.AspNetCore.Razor" Version="2.2.0" />    <PackageReference Include="Microsoft.AspNetCore.Razor.Design" Version="2.2.0" />  </ItemGroup></Project>

注：如果不做此修改，最后项目编译之后，不会产生预编译的Razor视图程序集。（这里如果有其他更优雅的修改方式，请大家留言， 我后续会先尝试先编写一个项目模板来避免这个重复操作）。

下面我们开始编写我们的插件。

这里我们首先创建一个Plugin1Controller.cs.

    public class Plugin1Controller : Controller    {        public IActionResult HelloWorld()        {            return View();        }    }

然后我们添加一个对应的视图文件HelloWorld.cshtml。

@{}<h1>This is Demo Plugin1.</h1>

最终项目文件目录如下：

最后我们需要修改一个项目的输出目录，我们需要将项目编译的dll发送到DynamicPluginsDemoSite项目的Debug目录中。

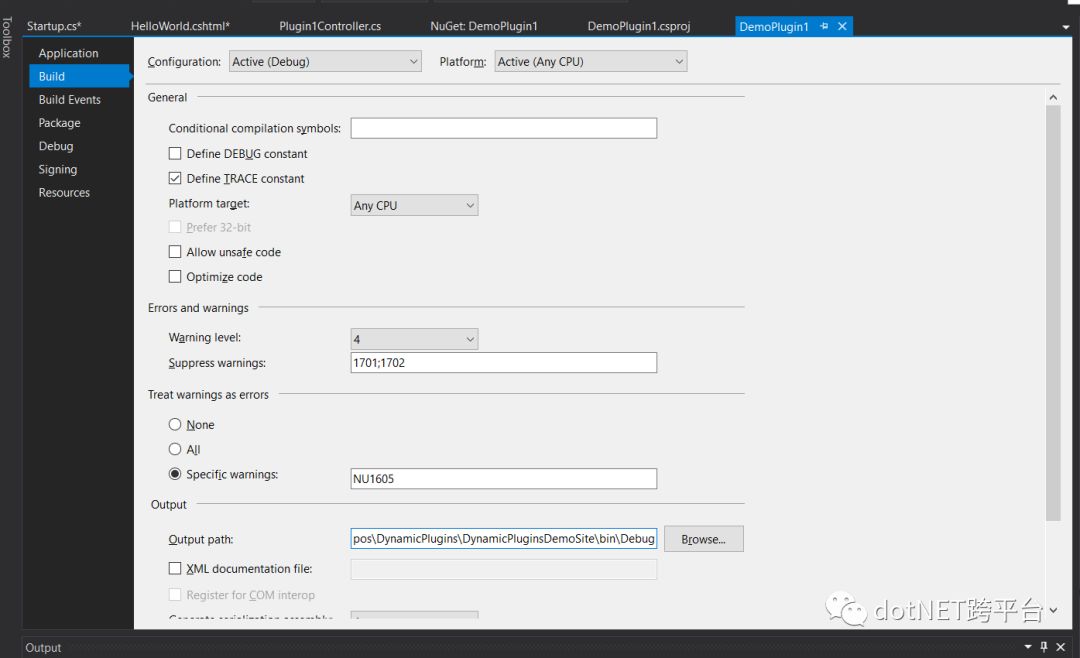
以上我们就完成了第一个组件的所有修改，下面我们开始修改DynamicPluginsDemoSite项目。

由于DynamicPluginsDemoSite项目不能直接引用DemoPlugin1, 所以当项目启动时，不能自主发现DemoPlugin1项目中的控制器，所以这里我们需要使用ApplicationPart将DemoPlugin1的程序集加载到当前的运行环境中。

public void ConfigureServices(IServiceCollection services){    services.Configure<CookiePolicyOptions>(options =>    {                options.CheckConsentNeeded = context => true;        options.MinimumSameSitePolicy = SameSiteMode.None;    });    var assembly = Assembly.LoadFile(AppDomain.CurrentDomain.BaseDirectory + "DemoPlugin1.dll");    var mvcBuilders = services.AddMvc();    var controllerAssemblyPart = new AssemblyPart(assembly);    mvcBuilders.ConfigureApplicationPartManager(apm =>    {        apm.ApplicationParts.Add(controllerAssemblyPart);    });    mvcBuilders.SetCompatibilityVersion(CompatibilityVersion.Version_2_2);}

代码解释:

• 由于前一步中， 我们将DemoPlugin1的程序集输出到了DynamicPluginsDemoSite的Debug目录中，所以这里我们可以使用Assembly.LoadFile方法将它加载。

• 这里我们使用AssemblyPart类，将加载程序集封装成一个ApplicationPart.

• mvcBuilders对象的ConfigureApplicationPartManager方法可以用来配置当前项目中使用的ApplicationPart

加载完控制器之后，我们还需要加载插件的预编译Razor视图。这里和之前的稍有不同，我们需要使用CompileRazorAssemblyPart来封装加载的预编译Razor视图。

public void ConfigureServices(IServiceCollection services){    services.Configure<CookiePolicyOptions>(options =>    {                options.CheckConsentNeeded = context => true;        options.MinimumSameSitePolicy = SameSiteMode.None;    });    var assembly = Assembly.LoadFile(AppDomain.CurrentDomain.BaseDirectory + "DemoPlugin1.dll");    var assemblyView = Assembly.LoadFile(AppDomain.CurrentDomain.BaseDirectory + "DemoPlugin1.Views.dll");    var viewAssemblyPart = new CompiledRazorAssemblyPart(assemblyView);    var controllerAssemblyPart = new AssemblyPart(assembly);    var mvcBuilders = services.AddMvc();    mvcBuilders.ConfigureApplicationPartManager(apm =>    {        apm.ApplicationParts.Add(controllerAssemblyPart);        apm.ApplicationParts.Add(viewAssemblyPart);    });    mvcBuilders.SetCompatibilityVersion(CompatibilityVersion.Version_2_2);}

现在我们启动DynamicPluginsDemoSite，在浏览器中输入/Plugin1/HelloWorld, 我们的插件就正常启用了。

注意：在启动DynamicPluginsDemoSite站点之前，请务必先编译DemoPlugin1项目，这样DemoPlugin1产生的程序集才会输出到DynamicPluginsDemoSite中。

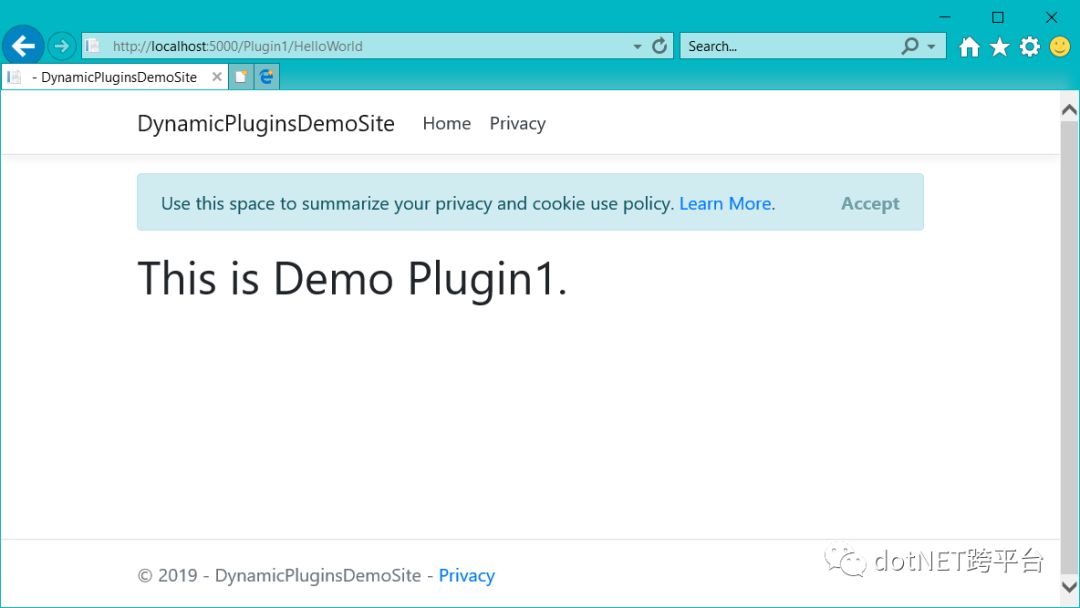
以上只是实现了一个最简单的MVC插件功能，要想完善整个项目，后续还有很多工作要做

• 需要创建一个插件模板，来避免一些重复操作。

• 需要将插件的模型和业务抽象出来。

• 需要改用数据库来保存插件信息。

• 需要支持实现插件的管理以及插件的升级。

后续我会慢慢实现以上功能，大家敬请期待。

原文地址：https://www.cnblogs.com/lwqlun/p/11137788.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com