引入

K-D Tree 是一种处理高维空间的数据结构。

支持$O(n^{\frac{k-1}{k}})$查询给定超矩形内的点的信息， $k$ 为维数。

可以用替罪羊树的思想实现动态插入。

但其实用的最多的是在错误的复杂度内查询奇奇怪怪的点信息。

构建

K-D Tree 是平衡树的结构（但应该不能叫平衡树）。

它的核心思想是通过树一层层的分化，把整个空间分割成若干子空间。

但是点是$k$维的，而树只有二维，所以一次我们只能选择一维来划分。

我们关心的问题是如何选取进行比较的维度。

一种方法是选取方差最大的维度，但在OI中不常用

OI中一般轮流选取，即深度为$d$的结点按第$d\%k$维的坐标划分

具体而言，设点的序列为$p$,对于一个需要构建区间 $[L,R]$，设当前需要分的维度为$d$

如果 $L=R$ ,那么划分出的只有当前一个点

为了保证尽量均匀，我们选取这一维的中位数作为当前子树的根

设 mid=(l+r)/2

可以使用 C++ STL 中一个奥妙重重的函数 nth_element

它可以把第 $k$ 小的元素放在第 $k$ 位，然后比它小的放在左边（但并不保证有序，后同），比它大的放在右边。复杂度为 $O(n)$ （其实就是阉割版的快排）

这样我们 nth_element(p+l,p+mid,p+r+1) 就完事了

因为已经帮你分好了 ，所以把中位数间个点当根，然后递归 $[L,mid-1]$ 和 $[mid+1,R]$

最后更新子树信息，我们要维护的是超矩形，记录一下每一维的最小值和最大值就可以了。

复杂度 $O(n\log n)$

插入

用平衡树的方法插入，根据当前层数判断往左还是往右

当然可能会插成链，你又不能旋转，所以只能考虑重构

暴力推平重新建就可以了，没啥技术含量

只是重建带一个 $\log$ ，所以可能跑得有点慢……

询问

询问一个 $k$ 维超矩形内所有点的信息

用线段树的思想无脑递归就可以了

如果完全包含当前点划分出的子空间直接返回当前子树的值，没有相交返回 $0$

复杂度可以证明是$O(n^{1-\frac{1}{k}})$

对于 $k=2$ 的情况提供一个不知道对不对的证明：

对于一个结点，设其子树大小为$n$,我们考虑往下分两层

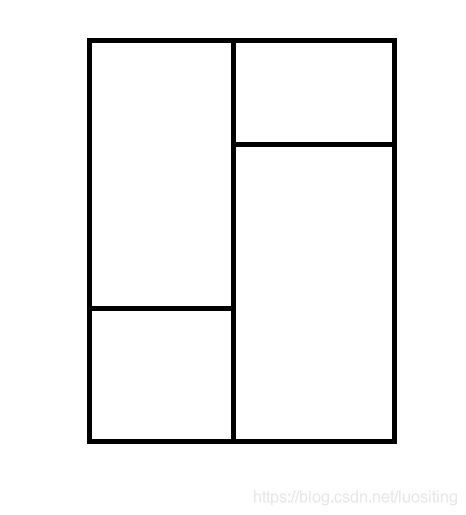
设$T_1(n)$表示询问中间挖一块的复杂度

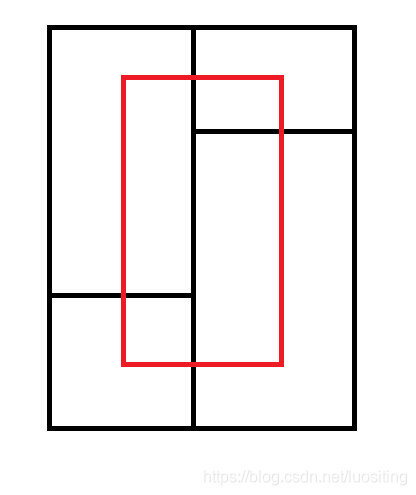
$T_2(n)$表示挖一个角的复杂度

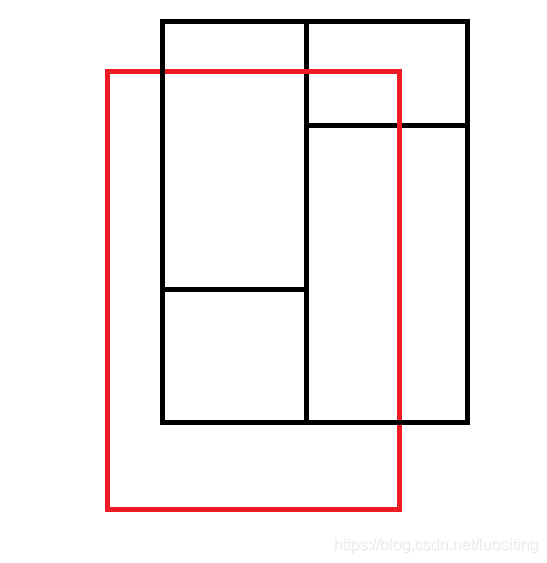
$T_3(n)$为平行挖的复杂度

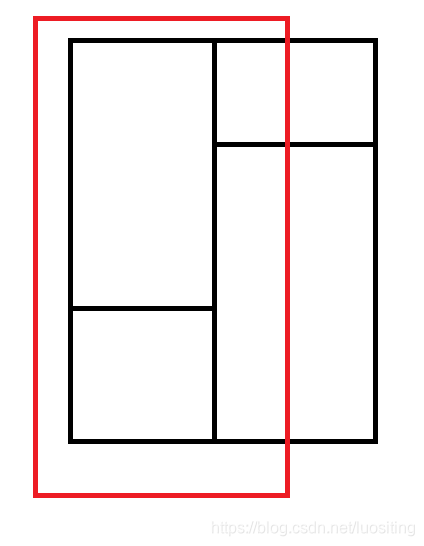
显然有

$$\begin{gathered} T_1(n)=4T_2(\frac{n}{4}) \\ {T}_2(n)=2T_3(\frac{n}{4})+T_2(\frac{n}{4}) \\ {T}_3(n)=2T_3(\frac{n}{4}) \end{gathered}$$

解得

$$T_1(n)=T_2(n)=T_3(n)=\sqrt{n}$$

有一些变种，比如一次函数的下方、最近点对，但这些复杂度都是错的。

不过如果出题人不刻意卡跑得还是挺快的，是个骗分的不错选择（

例题

Luogu4148 简单题

有一个$n\times n$的方阵，开始时值都为$0$,维护$m$次操作：

1. 在$(x,y)$的位置加上$v$
2. 询问一个矩阵内的数字和

$n\le 5\times 10^5,m\le 2\times 10^5$

强制在线，空间限制20M

模板题

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cctype>
#include <algorithm>
#define MAXN 200005
using namespace std;
inline int read()
{int ans=0;char c=getchar();while (!isdigit(c)) c=getchar();while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();return ans;
}
const double alpha=0.7;
struct point{int x[2];point(const int& a=0,const int& b=0){x[0]=a,x[1]=b;}};
inline point min(const point& a,const point& b){return point(min(a.x[0],b.x[0]),min(a.x[1],b.x[1]));}
inline point max(const point& a,const point& b){return point(max(a.x[0],b.x[0]),max(a.x[1],b.x[1]));}
inline bool operator ==(const point& a,const point& b){return a.x[0]==b.x[0]&&a.x[1]==b.x[1];}
int val[MAXN],sum[MAXN],siz[MAXN],ch[MAXN][2],tot;
point cur[MAXN],L[MAXN],R[MAXN];
int rt,*tag,dir;
int rub[MAXN];
inline int newnode(const int& v,const point& p)
{int x=rub[0]? rub[rub[0]--]:++tot;val[x]=sum[x]=v,siz[x]=1,cur[x]=L[x]=R[x]=p;ch[x][0]=ch[x][1]=0;return x;
}
inline void update(const int& x)
{sum[x]=val[x]+sum[ch[x][0]]+sum[ch[x][1]];siz[x]=siz[ch[x][0]]+siz[ch[x][1]]+1;L[x]=min(cur[x],min(L[ch[x][0]],L[ch[x][1]]));R[x]=max(cur[x],max(R[ch[x][0]],R[ch[x][1]]));
}
void insert(int& x,int k,int v,const point& p)
{if (!x) return (void)(x=newnode(v,p));if (cur[x]==p) return val[x]+=v,update(x);int d=p.x[k]<cur[x].x[k];insert(ch[x][d],k^1,v,p);update(x);if (siz[ch[x][d]]>siz[x]*alpha) tag=&x,dir=k;
}
struct node{int v;point p;};
node buf[MAXN];
int cnt;
int cur_k;
inline bool operator <(const node& a,const node& b){return a.p.x[cur_k]<b.p.x[cur_k];}
void build(int& x,int k,int l,int r)
{if (l>r) return (void)(x=0);int mid=(l+r)>>1;cur_k=k,nth_element(buf+l,buf+mid,buf+r+1);x=newnode(buf[mid].v,buf[mid].p);build(ch[x][0],k^1,l,mid-1),build(ch[x][1],k^1,mid+1,r);update(x);
}
void dfs(int x)
{if (!x) return;dfs(ch[x][0]);buf[++cnt].p=cur[x],buf[cnt].v=val[x],rub[++rub[0]]=x;dfs(ch[x][1]);
}
inline void rebuild()
{cnt=0;dfs(*tag);build(*tag,dir,1,cnt);
}
int query(int x,point l,point r)
{if (l.x[0]<=L[x].x[0]&&R[x].x[0]<=r.x[0]&&l.x[1]<=L[x].x[1]&&R[x].x[1]<=r.x[1]) return sum[x];if (r.x[0]<L[x].x[0]||R[x].x[0]<l.x[0]||r.x[1]<L[x].x[1]||R[x].x[1]<l.x[1]) return 0;int ans=0;if (l.x[0]<=cur[x].x[0]&&cur[x].x[0]<=r.x[0]&&l.x[1]<=cur[x].x[1]&&cur[x].x[1]<=r.x[1]) ans=val[x];return ans+query(ch[x][0],l,r)+query(ch[x][1],l,r);
}
int main()
{memset(L,0x7f,sizeof(L));read();int lans=0;while (true){int x1,y1,x2,y2,v;switch(read()){case 1:x1=read()^lans,y1=read()^lans,v=read()^lans;tag=NULL;insert(rt,0,v,point(x1,y1));if (tag!=NULL) rebuild();break;case 2:x1=read()^lans,y1=read()^lans,x2=read()^lans,y2=read()^lans;printf("%d\n",lans=query(rt,point(x1,y1),point(x2,y2)));break;case 3:return 0;}}
} 

Luogu4475 巧克力王国

题意：给定$n$对$x_i,y_i$,$m$次询问，每次给定$a,b,c$,求$ax+by<c$的$(x,y)$的个数

$n,m\le 5\times 10^4,-10^9\le x,y,a,b,c\le 10^9$

先口胡一份

显然满足条件的$(x,y)$在一个一次函数下方

建出K-D Tree后，询问时因为是矩形，如果四个点都在这个函数下方，那么整个矩形中的点都在下方，直接返回

注意这个复杂度是错误的，只是数据没卡跑得快