题意：$n$个点带边权的树，动态修改点权$v_i$，最小化 钦定一个点$x$ 后 $\sum _{i}dist(x,i)\ast v_i$的值。

$n,q\le 10^5$，度数不超过$20$

限制度数的树上的一些诡异的操作，时限很长，多半是点分树。

也叫动态点分治，但实际上并不是动态的点分治并且有一定误导性，所以以后都叫点分树。

点分树是对一个树点分治后的结构建出的树，即在点分治时将下一层的重心的父亲设为当前的分治中心。

它具有以下常用的性质：

1. 原树与点分树 一个相同的点$u$的儿子$v$为根的子树 一一对应。
2. 点分树上两个点的$lca$ 在原树上这两个点的路径上。
3. 树高$O(\log n)$

本质上是对树建出的线段树。

在本题中详细讲解。

首先本题实际上求的是带权重心

有个结论：

设当前点是$u$,如果$v$比$u$更优

那么有

$$len(u,v)\ast (n-su{m}_v-su{m}_v)<0$$

其中$sum$表示子树点权和

即

$$2su{m}_v>n$$

然后继续往下走

不难看出对于一个$u$，这样的$v$最多只有$1$个，所以答案一定在满足条件的$v$的子树内。如果没有这样的$v$说明$u$是带权重心。

这样是$O(n)$的，考虑搬到点分树上

从点分树的根开始往下走

设当前在$u$,我们找到点分树上$u$的一个儿子$v$

注意之前的结论只能往原树上相邻的点走，所以你不能直接用这个结论判断$v$

但是如果我们设$u$往 $v$在点分树上的子树 的这个方向走一步 到达的点是$w$

即：

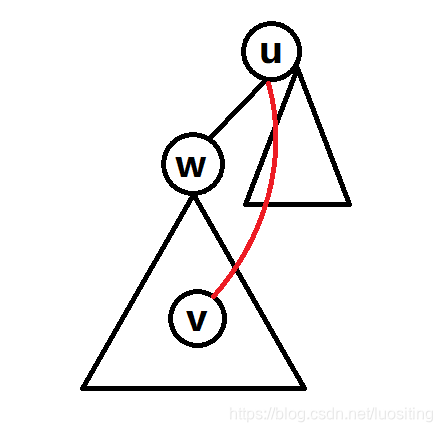
（红色为点分树）

因为$w$在原树上的子树 等于 $v$在点分树上的子树

我们想判断答案是否在 $v$在点分树上的子树内，可以转换为是否在 $w$在原树上的子树内

然而如果你判$2\ast su{m}_v>su{m}_{rt}$,会发现你还是WA了

原因是你钦定$u$为根之后，这棵树的形态已经确定了

你在点分树上一直往下走，实际上原树上仍然在乱跳

人话：只有第一层的$w$（原树）和$v$（点分树）的子树一样，后面的点分树上的子树在原树上甚至可能不是子树。

但是上面已经证明过最多只有一个$v$

我们可以直接算出$u$在原树上的每个儿子的答案和根结点比较，如果有一个$w$比根结点优，因为只有一个，说明答案在 $w$在原树上的子树（或$v$在点分树上的子树）内。

然后想象把这条边断开，化归到从$v$开始的子问题。

也就是说$u$和$v$并没有实质关联，只是从重心开始方便处理而已。

现在考虑如何计算一个点的答案

维护$an{s}_u$表示以$f{a}_u$为根时，$u$在点分树上的子树中的点到$f{a}_u$的帯权距离（距离*点权）之和，$fa$为在点分树上的父结点。

询问点$x$的答案时，先加入点分树上子结点的所有$ans$,然后在点分树上往上跳，把兄弟结点的子树中的所有点权挪到父亲上，再一起挪到$x$。因为树高$O(\log n)$，可以保证复杂度。详见代码。

修改的时候暴力跳父亲修改$sum$和$ans$就可以了。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cctype>
#include <vector>
#include <cassert>
#define MAXN 100005
#define MAXM 200005
using namespace std;
typedef long long ll;
inline int read()
{int ans=0,f=1;char c=getchar();while (!isdigit(c)) (c=='-')&&(f=-1),c=getchar();while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();return f*ans;
}
struct edge{int u,v,w;}e[MAXM];
int head[MAXN],nxt[MAXM],cnt;
void addnode(int u,int v,int w)
{e[++cnt]=(edge){u,v,w};nxt[cnt]=head[u];head[u]=cnt;
}
int dis[MAXN],pos[MAXN],dfn[MAXM],up[MAXN],tim;
void dfs(int u)
{dfn[pos[u]=++tim]=u;for (int i=head[u];i;i=nxt[i])if (!pos[e[i].v]){dis[e[i].v]=dis[u]+e[i].w;up[e[i].v]=u;dfs(e[i].v);dfn[++tim]=u;}
}
int LOG[MAXM],st[20][MAXM];
inline int Min(const int& x,const int& y){return pos[x]<pos[y]? x:y;}
inline void init()
{LOG[0]=-1;for (int i=1;i<MAXM;i++) LOG[i]=LOG[i>>1]+1;for (int i=1;i<=tim;i++) st[0][i]=dfn[i];for (int i=1;i<20;i++)for (int j=1;j+(1<<(i-1))<=tim;j++)st[i][j]=Min(st[i-1][j],st[i-1][j+(1<<(i-1))]);
}
inline int lca(const int& x,const int& y)
{int l=pos[x],r=pos[y];if (l>r) swap(l,r);int t=LOG[r-l+1];return Min(st[t][l],st[t][r-(1<<t)+1]);
}
inline int dist(const int& x,const int& y){return dis[x]+dis[y]-2*dis[lca(x,y)];}
int rt;
int siz[MAXN],maxp[MAXN]={0x7fffffff};
bool cut[MAXN];
void findrt(int u,int f,int sum)
{siz[u]=1,maxp[u]=0;for (int i=head[u];i;i=nxt[i])if (e[i].v!=f&&!cut[e[i].v]){findrt(e[i].v,u,sum);siz[u]+=siz[e[i].v],maxp[u]=max(maxp[u],siz[e[i].v]);}if (sum-siz[u]>maxp[u]) maxp[u]=sum-siz[u];if (maxp[u]<maxp[rt]) rt=u;
}
int getsiz(int u,int f)
{int ans=1;for (int i=head[u];i;i=nxt[i])if (e[i].v!=f&&!cut[e[i].v])ans+=getsiz(e[i].v,u);return ans;
}
int d[MAXN],sum[MAXN];
ll ans[MAXN];
int fa[MAXN];
vector<int> son[MAXN],top[MAXN];
void build()
{int u=rt;cut[u]=true;for (int i=head[u];i;i=nxt[i])if (!cut[e[i].v]){rt=0;findrt(e[i].v,0,getsiz(e[i].v,0));son[u].push_back(rt),top[u].push_back(e[i].v),fa[rt]=u;build();}
}
bool vis[MAXN];
void DFS(int u)
{assert(!vis[u]);vis[u]=true;for (int i=0;i<(int)son[u].size();i++)DFS(son[u][i]);
}
inline void modify(int x,int v)
{int u=x;for (;fa[x];x=fa[x]) sum[x]+=v,ans[x]+=(ll)dist(fa[x],u)*v;sum[x]+=v;
}
inline ll calc(int x)
{ll res=0;for (int i=0;i<(int)son[x].size();i++)res+=ans[son[x][i]];for (int u=fa[x],v=x;u;v=u,u=fa[u]){int tot=d[u];for (int i=0;i<(int)son[u].size();i++)if (son[u][i]!=v)res+=ans[son[u][i]],tot+=sum[son[u][i]];res+=(ll)tot*dist(u,x);		}return res;
}
inline ll query(int x)
{ll v=calc(x);for (int i=0;i<(int)son[x].size();i++)if (calc(top[x][i])<v)return query(son[x][i]);return v;
}
int main()
{int n,q;n=read(),q=read();for (int i=1;i<n;i++){int u,v,w;u=read(),v=read(),w=read();addnode(u,v,w),addnode(v,u,w);}dfs(1);init();int Rt;findrt(1,0,n),Rt=rt,build();while (q--){int x,v;x=read(),v=read();d[x]+=v,modify(x,v);printf("%lld\n",query(Rt));}return 0;
}