一、SGD

右边的值更新左边的值，每次更新朝着梯度方向前进一小步。

class SGD:"""随机梯度下降法（Stochastic Gradient Descent）"""def __init__(self, lr=0.01):self.lr = lrdef update(self, params, grads):for key in params.keys():params[key] -= self.lr * grads[key] 

二、Momentum-动量

SGD实现简单，有些问题可能没有效果，比如f(x,y)=(1/20)x^ 2 +y ^2

SGD低效的根本原因：梯度的方向没有指向最小值的方向。如果函数形状非均向，如呈现延伸状，搜索路径就非常低效，有可能呈现z字形移动。

Momentum-动量方法公式：

v表示物体在梯度方向受的力，αv作用是让物体逐渐减速(α小于1，常数，如0.9之类的数)。

动量法的好处，x轴方向受力小，但是每一次梯度变化的方向不变，速度方向不变，一直在这个方向受力，往那个方向走的速度会加速。但是y轴受到正反方向的力，他们会抵消，让y不稳定，因此和SGD相比，能更快的向x轴方向靠近。

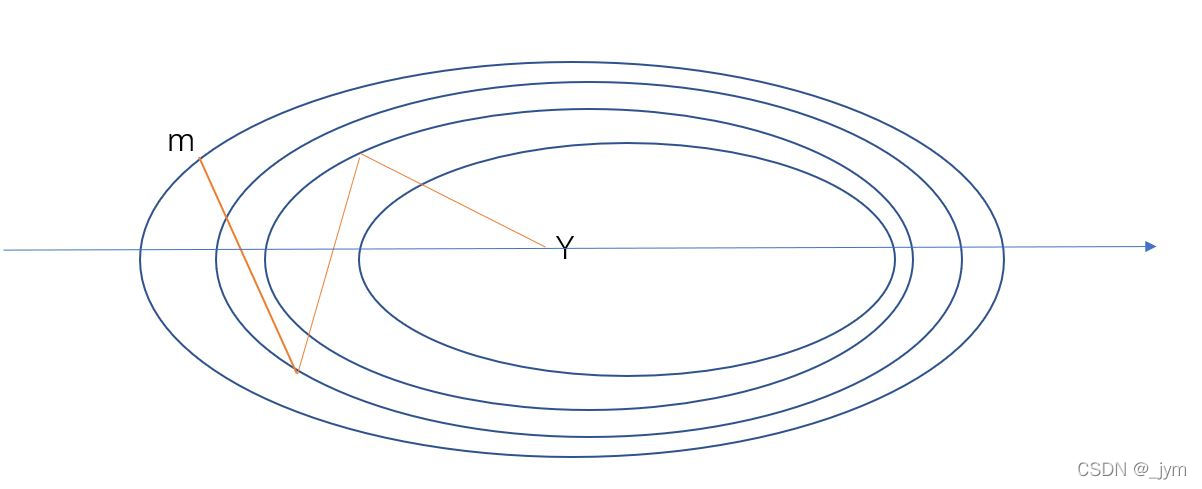
简的来说，SGD的话就是他y方向梯度大，步子跨的猛的话就z形了，动量的目的是梯度大的那块，迈步子时候让它考虑到上一次的步子是往哪走的。如果相反方向走的话，其实是抵消了一部分v，这样的话如果步子跨得猛，他也得少一点步子。如下图所示，对于f(x,y)=(1/20)x^ 2 +y ^2用SGD的话，m想走到y，它在y轴摇摆的厉害，但是，用动量，y轴摇摆抵消了，而且x轴速度还增加了，多好。

class Momentum:"""Momentum SGD"""def __init__(self, lr=0.01, momentum=0.9):self.lr = lrself.momentum = momentumself.v = Nonedef update(self, params, grads):if self.v is None:self.v = {}for key, val in params.items():                                self.v[key] = np.zeros_like(val)for key in params.keys():self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] params[key] += self.v[key]

三、AdaGrad

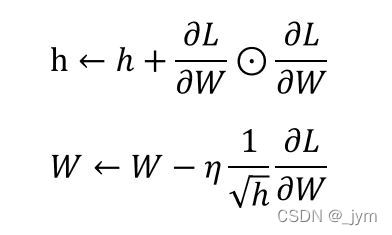
h保存了梯度的平方和，圆圈就表示矩阵相乘。

由于乘上根号h分之1，参数的元素中，变动较大的元素的学习率将变小。

这是一种学习率衰减的手法，梯度下降太快了，山谷太陡峭了，那我就让你走的步子减小，这样一来，你不容易直接一步跨俩山峰（山峰是啥懂得都懂，嘿嘿）。

class AdaGrad:"""AdaGrad"""def __init__(self, lr=0.01):self.lr = lrself.h = Nonedef update(self, params, grads):if self.h is None:self.h = {}for key, val in params.items():self.h[key] = np.zeros_like(val)for key in params.keys():self.h[key] += grads[key] * grads[key]params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

四、Adam

结合了Momentum和AdaGrad方法。

看代码去吧

很多人喜欢用Adam哦

class Adam:"""Adam (http://arxiv.org/abs/1412.6980v8)"""def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):self.lr = lrself.beta1 = beta1self.beta2 = beta2self.iter = 0self.m = Noneself.v = Nonedef update(self, params, grads):if self.m is None:self.m, self.v = {}, {}for key, val in params.items():self.m[key] = np.zeros_like(val)self.v[key] = np.zeros_like(val)self.iter += 1lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)         for key in params.keys():#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)#unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias#unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias#params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)