基于卷积神经网络的手写数字识别、python实现

一、CNN网络结构与构建

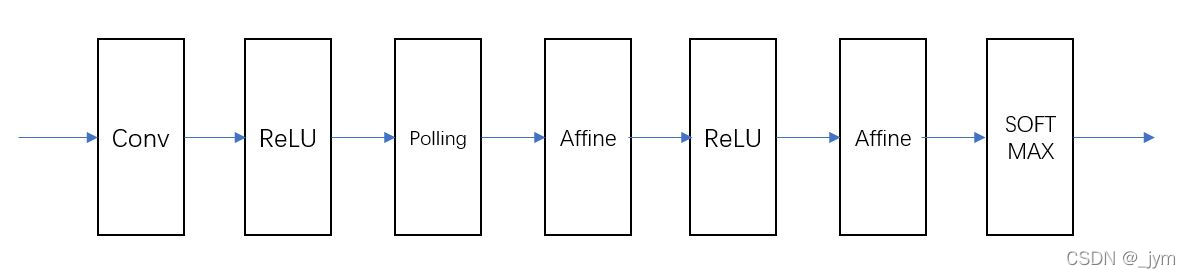
在这里插入图片描述

参数：

输入数据的维数，通道，高，长

input_dim=(1, 28, 28)

卷积层的超参数，filter_num：滤波器数量，filter_size：滤波器大小，stride：步幅，pad，填充。

 conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1}

hidden_size，隐藏层全连接神经元数量；

output_size，输出层全连接神经元数量；

weight_init_std，初始化时，权重的标准差；

hidden_size=100, output_size=10, weight_init_std=0.01

学习所需参数是第一层的卷积层和剩余两个全连接层的权重和偏置。权重、偏置，分别用W、b保存。

self.params = {}self.params['W1'] = weight_init_std * \np.random.randn(filter_num, input_dim[0], filter_size, filter_size)self.params['b1'] = np.zeros(filter_num)self.params['W2'] = weight_init_std * \np.random.randn(pool_output_size, hidden_size)self.params['b2'] = np.zeros(hidden_size)self.params['W3'] = weight_init_std * \np.random.randn(hidden_size, output_size)self.params['b3'] = np.zeros(output_size)

代码：

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import pickle
import numpy as np
from collections import OrderedDict
from common.layers import *
from common.gradient import numerical_gradientclass SimpleConvNet:"""简单的ConvNetconv - relu - pool - affine - relu - affine - softmaxParameters----------input_size : 输入大小（MNIST的情况下为784）hidden_size_list : 隐藏层的神经元数量的列表（e.g. [100, 100, 100]）output_size : 输出大小（MNIST的情况下为10）activation : 'relu' or 'sigmoid'weight_init_std : 指定权重的标准差（e.g. 0.01）指定'relu'或'he'的情况下设定“He的初始值”指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”"""def __init__(self, input_dim=(1, 28, 28), conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},hidden_size=100, output_size=10, weight_init_std=0.01):filter_num = conv_param['filter_num']filter_size = conv_param['filter_size']filter_pad = conv_param['pad']filter_stride = conv_param['stride']input_size = input_dim[1]conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))# 初始化权重self.params = {}self.params['W1'] = weight_init_std * \np.random.randn(filter_num, input_dim[0], filter_size, filter_size)self.params['b1'] = np.zeros(filter_num)self.params['W2'] = weight_init_std * \np.random.randn(pool_output_size, hidden_size)self.params['b2'] = np.zeros(hidden_size)self.params['W3'] = weight_init_std * \np.random.randn(hidden_size, output_size)self.params['b3'] = np.zeros(output_size)# 生成层self.layers = OrderedDict()self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],conv_param['stride'], conv_param['pad'])self.layers['Relu1'] = Relu()self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])self.layers['Relu2'] = Relu()self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])self.last_layer = SoftmaxWithLoss()def predict(self, x):for layer in self.layers.values():x = layer.forward(x)return xdef loss(self, x, t):"""求损失函数参数x是输入数据、t是教师标签"""y = self.predict(x)return self.last_layer.forward(y, t)def accuracy(self, x, t, batch_size=100):if t.ndim != 1 : t = np.argmax(t, axis=1)acc = 0.0for i in range(int(x.shape[0] / batch_size)):tx = x[i*batch_size:(i+1)*batch_size]tt = t[i*batch_size:(i+1)*batch_size]y = self.predict(tx)y = np.argmax(y, axis=1)acc += np.sum(y == tt) return acc / x.shape[0]def numerical_gradient(self, x, t):"""求梯度（数值微分）Parameters----------x : 输入数据t : 教师标签Returns-------具有各层的梯度的字典变量grads['W1']、grads['W2']、...是各层的权重grads['b1']、grads['b2']、...是各层的偏置"""loss_w = lambda w: self.loss(x, t)grads = {}for idx in (1, 2, 3):grads['W' + str(idx)] = numerical_gradient(loss_w, self.params['W' + str(idx)])grads['b' + str(idx)] = numerical_gradient(loss_w, self.params['b' + str(idx)])return gradsdef gradient(self, x, t):"""求梯度（误差反向传播法）Parameters----------x : 输入数据t : 教师标签Returns-------具有各层的梯度的字典变量grads['W1']、grads['W2']、...是各层的权重grads['b1']、grads['b2']、...是各层的偏置"""# forwardself.loss(x, t)# backwarddout = 1dout = self.last_layer.backward(dout)layers = list(self.layers.values())layers.reverse()for layer in layers:dout = layer.backward(dout)# 设定grads = {}grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].dbgrads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].dbgrads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].dbreturn gradsdef save_params(self, file_name="params.pkl"):params = {}for key, val in self.params.items():params[key] = valwith open(file_name, 'wb') as f:pickle.dump(params, f)def load_params(self, file_name="params.pkl"):with open(file_name, 'rb') as f:params = pickle.load(f)for key, val in params.items():self.params[key] = valfor i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):self.layers[key].W = self.params['W' + str(i+1)]self.layers[key].b = self.params['b' + str(i+1)]

二、使用CNN网络学习MNIST数据集并观察效果

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from simple_convnet import SimpleConvNet
from common.trainer import Trainer# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False)# 处理花费时间较长的情况下减少数据 
x_train, t_train = x_train[:5000], t_train[:5000]
x_test, t_test = x_test[:1000], t_test[:1000]max_epochs = 20network = SimpleConvNet(input_dim=(1,28,28), conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},hidden_size=100, output_size=10, weight_init_std=0.01)trainer = Trainer(network, x_train, t_train, x_test, t_test,epochs=max_epochs, mini_batch_size=100,optimizer='Adam', optimizer_param={'lr': 0.001},evaluate_sample_num_per_epoch=1000)
trainer.train()# 保存参数
network.save_params("params.pkl")
print("Saved Network Parameters!")# 绘制图形
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
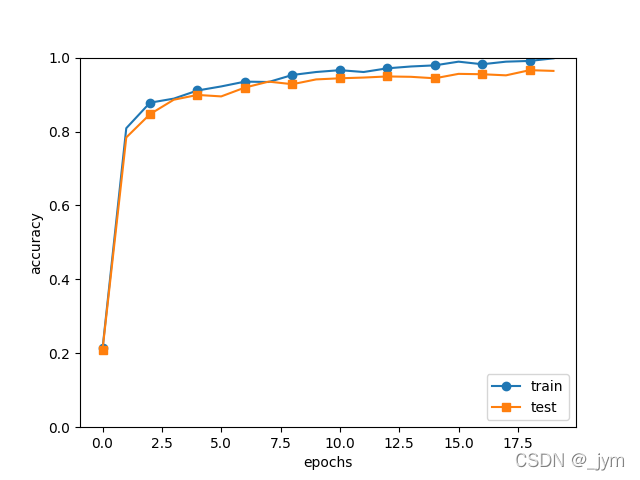
plt.plot(x, trainer.train_acc_list, marker='o', label='train', markevery=2)
plt.plot(x, trainer.test_acc_list, marker='s', label='test', markevery=2)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()

效果：

=== epoch:20, train acc:0.998, test acc:0.964 ===
train loss:0.007401310521311435
train loss:0.027614604405772653
train loss:0.010395290280106407
train loss:0.009055562731122933
train loss:0.010614723913692073
train loss:0.012437935682767121
train loss:0.026701506796337437
train loss:0.006204184557258094
train loss:0.010404145189650856
train loss:0.010929826675443866
train loss:0.0043394220957300835
train loss:0.016781798147762927
train loss:0.008747950916926508
train loss:0.022275261048058662
train loss:0.004475751241820642
train loss:0.018634365845167887
train loss:0.010216296159200803
train loss:0.05663255540517016
train loss:0.007190307798334322
train loss:0.05278721478973261
train loss:0.01059534308178735
train loss:0.005966098495078249
train loss:0.010178506340940181
train loss:0.03654597399370525
train loss:0.019495820002866274
train loss:0.01572182958630932
train loss:0.00465907402610126
train loss:0.024876708101982406
train loss:0.005049280179694557
train loss:0.014516301412561905
train loss:0.007808137131314081
train loss:0.0400124952112783
train loss:0.014341889140004867
train loss:0.007797598015128371
train loss:0.02575987545665843
train loss:0.08519312577327812
train loss:0.021226771077661372
train loss:0.004566285129776959
train loss:0.014989958271037414
train loss:0.015107332850379906
train loss:0.017502483559764623
train loss:0.008879393649119861
train loss:0.013326281023352782
train loss:0.021570154414811325
train loss:0.010967106033868279
train loss:0.039365545329473575
train loss:0.03687669299007644
train loss:0.005511731850415302
train loss:0.005646337734962965
=============== Final Test Accuracy ===============
test acc:0.963

测试数据识别率百分之九十多，可见识别率还是挺不错的。

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/560235.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

基于深度学习的手写数字识别、python实现

基于深度学习的手写数字识别、python实现

基于深度学习的手写数字识别、python实现一、what is 深度学习二、加深层可以减少网络的参数数量三、深度学习的手写数字识别一、what is 深度学习 深度学习是加深了层的深度神经网络。 二、加深层可以减少网络的参数数量 加深层的网络可以用更少参数获得与没有加深层同等水…
阅读更多...
二极管的结构、特性、参数、稳压管的特性和参数

二极管的结构、特性、参数、稳压管的特性和参数

二极管的结构、特性、参数、稳压管的特性和参数本文介绍的定义一、半导体类型二、PN结的结构与单向导电性三、二极管的伏安特性四、二极管的参数五、稳压管本文介绍的定义 本文介绍的定义：半导体、本征半导体、空穴、载流子、杂质半导体、N型半导体、P型半导体、PN…
阅读更多...
双极结型三极管的结构、特性曲线、参数、lceda仿真

双极结型三极管的结构、特性曲线、参数、lceda仿真

双极结型三极管的结构、特性、参数本文介绍的定义一、三极管结构二、三极管特性曲线三、三极管参数本文介绍的定义 硅平面管、锗合金管、发射区、基区，集电区、发射极、基极、集电极、发射结、集电结、发射、发射极电流、复合和扩散、基极电流、收集、集电极电流、…
阅读更多...
结型场效应管的结构、特性、参数

结型场效应管的结构、特性、参数

结型场效应管的结构、特性、参数本文介绍的定义一、N沟道结型场效应管结构二、N沟道结型场效应管特性曲线本文介绍的定义 场效应管、结型场效应管、N沟道结型场效应管的结构、耗尽层、栅极、源极、漏极、N沟道结型场效应管、夹断电压、预夹断、输出特性、可变电阻区、恒流区、…
阅读更多...
绝缘栅型场效应管的结构、特性、参数

绝缘栅型场效应管的结构、特性、参数

绝缘栅型场效应管的结构、特性、参数本文介绍的定义一、N沟道增强型MOS场效应管结构二、N沟道增强型MOS场效应管特性曲线三、N沟道耗尽型MOS场效应管结构和特性曲线本文介绍的定义 绝缘栅型场效应管、N沟道增强型MOS场效应管、耗尽型场效应管、增强型场效应管、反型层、开启电…
阅读更多...
放大电路、单管共发射极放大电路结构、工作原理、lceda仿真

放大电路、单管共发射极放大电路结构、工作原理、lceda仿真

放大电路、单管共发射极放大电路结构、工作原理本文介绍的定义一、放大电路基本概念二、单管共发射极放大电路本文介绍的定义 放大、实现放大作用、放大电路技术指标测量、电压放大倍数、电流放大倍数、相量表示、最大输出幅度、峰峰值、非线性失真系数、输入电阻、输出电阻、…
阅读更多...
放大电路分析方法、图解法分析放大电路、lceda仿真

放大电路分析方法、图解法分析放大电路、lceda仿真

放大电路分析方法、图解法分析放大电路一、本文介绍的定义二、放大电路分析方法三、图解法一、本文介绍的定义 放大电路分析、图解法、微变等效电路法、静态分析、动态分析、直流通路、交流通路、单管共射放大电路的直流和交流通路、静态工作点、图解法分析静态、直流负载线、…
阅读更多...
通过共现矩阵和余弦相似度实现机器对单词的认知、python实现

通过共现矩阵和余弦相似度实现机器对单词的认知、python实现

通过共现矩阵和余弦相似度实现机器对单词的认知、python实现本文介绍的定义：一、语料库预处理二、单词的分布式表示三、单词的相似度四、相似单词排序本文介绍的定义： 语料库、计数方法的目的、语料库预处理、单词的分布式表示、分布式假设、上下文、窗…
阅读更多...
使用PPMI改进共现矩阵

使用PPMI改进共现矩阵

使用PPMI改进共现矩阵 共现矩阵的元素表示两个单词同时出现的次数，这里的次数并不具备好的性质，举个例子，有短语叫the car，因为the是个常用词，如果以两个单词同时出现的次数为衡量相关性的标准，与drive 相…
阅读更多...
基于SVD的降维优化

基于SVD的降维优化

基于SVD的降维优化 向量降维：尽量保留数据“重要信息”的基础上减少向量维度。可以发现重要的轴（数据分布广的轴），将二维数据 表示为一维数据，用新轴上的投影值来表示各个数据点的值，示意图如下。 稀疏矩阵…
阅读更多...
微变等效电路法分析放大电路

微变等效电路法分析放大电路

微变等效电路法分析放大电路本文介绍的定义一、简化的h参数微变等效电路1.静态工作点计算2.微变等效电路法估算电压放大倍数二、微变等效电路法应用本文介绍的定义 微变等效电路法、h参数微变等效电路、单管共射放大电路的微变等效电路、Rbe近似估算、微变等效电路法应用。 一…
阅读更多...
分压式静态工作点稳定电路

分压式静态工作点稳定电路

分压式静态工作点稳定电路本文介绍的定义：一、静态工作点稳定问题二、分压式静态工作点稳定电路本文介绍的定义： 静态工作点稳定问题、温度对三极管参数的影响、分压式静态工作点稳定电路、电流负反馈式工作点稳定电路、旁路电容、静态分析、动态分析。…
阅读更多...
双极型三极管共集电极、共基极放大电路

双极型三极管共集电极、共基极放大电路

双极型三极管共集电极、共基极放大电路本文介绍的定义共集电极放大电路共基极放大电路本文介绍的定义 双极型三极管放大电路的接法、共集电极放大电路、射极跟随器、带负载能力、共基极放大电路、改善频率响应。 共集电极放大电路 接法：根据输入信号与输出信号公…
阅读更多...
stm32使用DAP下载程序

stm32使用DAP下载程序

jym认为，会下载程序等于学会stm32，hahaha。 首先点这个魔术棒 接下来进行下面的设置： 配置Debug选项 配置Utilities选项 配置Degug-setting选项 选择目标板，flash大小由板子芯片型号决定，勾选reset and run&#xff…
阅读更多...
stm32 NVIC EXTI

stm32 NVIC EXTI

stm32 NVIC EXTINVICEXTI原理图main.cexti.hexti.cstm32f10x_it.cNVIC NVIC 是嵌套向量中断控制器，控制着整个芯片中断相关的功能，它跟内核紧密耦合，是内核里面的一个外设。配置中断的时候我们一般只用 ISER、ICER 和 IP 这三个寄存器&#…
阅读更多...
stm32 HSE HSI

stm32 HSE HSI

stm32 HSE HSI时钟树main.cclkconfig.hclkconfig.c时钟树 HSE_SetSysClock和HSI_SetSysClock这两个函数就是根据上面这个时钟树编写的。 main.c 这个实验是通过HSE或者HSI配置系统时钟，结果就是，用HSE比HSI灯闪的快点，因为代码设置的是使用…
阅读更多...
stm32 SysTick

stm32 SysTick

SysTick是系统定时器，属于 CM3 内核中的一个外设，内嵌在 NVIC 中。系统定时器是一个 24bit 的向下递减的计数器，计数器每计数一次的时间为 1/SYSCLK，一般设置系统时钟 SYSCLK 等于 72M。当重装载数值寄存器的值递减到 0 的时候&am…
阅读更多...
stm32 USART

stm32 USART

介绍的定义 串行通信、并行通信、全双工、半双工、单工、同步、异步、比特率、码元、波特率、TTL、RS232、DB9接口、DTE、DCE、协议层、USART、UART、CH340G芯片、USB。 通信基础 根据数据传送的方式，通讯可分为串行通讯与并行通讯。 串行通信：同一时…
阅读更多...
robot 用AP连PC

robot 用AP连PC

1.启动机器人 2.PC找到机器人的热点，连接 3.看机器人分配的电脑ip 4.打开putty软件，下图里面是机器人的ip。然后点击open 。 5.输入机器人用户名和密码，现在已经登陆进去了。 6.输入ifconfig查看网络状况
阅读更多...
robot连PCwifi、PC开Shell连robot

robot连PCwifi、PC开Shell连robot

用网线将机器人和路由器连接，登录路由器管理界面，获取机器人 IP 地址。 打开Xshell，新建会话，主机设成机器人IP。 输入机器人用户名和密码 然后pc通过ssh连接上机器人 用ifconfig查看当前网络连接状态。有线连接是192.168.0.108&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023