同学你好!本文章于2021年末编写,已与实际存在较大的偏差!
故在2022年末对本系列进行填充与更新,欢迎大家订阅最新的专栏,获取基于Pytorch1.10版本的理论代码(2023版)实现,
Pytorch深度学习·理论篇(2023版)目录地址为:
CSDN独家 | 全网首发 | Pytorch深度学习·理论篇(2023版)目录本专栏将通过系统的深度学习实例,从可解释性的角度对深度学习的原理进行讲解与分析,通过将深度学习知识与Pytorch的高效结合,帮助各位新入门的读者理解深度学习各个模板之间的关系,这些均是在Pytorch上实现的,可以有效的结合当前各位研究生的研究方向,设计人工智能的各个领域,是经过一年时间打磨的精品专栏!https://v9999.blog.csdn.net/article/details/127587345欢迎大家订阅(2023版)理论篇
以下为2021版原文~~~~

3.4. softmax回归
回归可以用于预测多少的问题。 比如预测房屋被售出价格,或者棒球队可能获得的胜场数,又或者患者住院的天数。
事实上,我们也对分类问题感兴趣:不是问“多少”,而是问“哪一个”:
-
某个电子邮件是否属于垃圾邮件文件夹?
-
某个用户可能注册或不注册订阅服务?
-
某个图像描绘的是驴、狗、猫、还是鸡?
-
某人接下来最有可能看哪部电影?
通常,机器学习实践者用分类这个词来描述两个有微妙差别的问题:
1. 我们只对样本的“硬性”类别感兴趣,即属于哪个类别;
2. 我们希望得到“软性”类别,即得到属于每个类别的概率。 这两者的界限往往很模糊。其中的一个原因是:即使我们只关心硬类别,我们仍然使用软类别的模型。
3.4.1. 分类问题
我们从一个图像分类问题开始。 假设每次输入是一个2×2的灰度图像。 我们可以用一个标量表示每个像素值,每个图像对应四个特征x1,x2,x3,x4。 此外,假设每个图像属于类别“猫”,“鸡”和“狗”中的一个。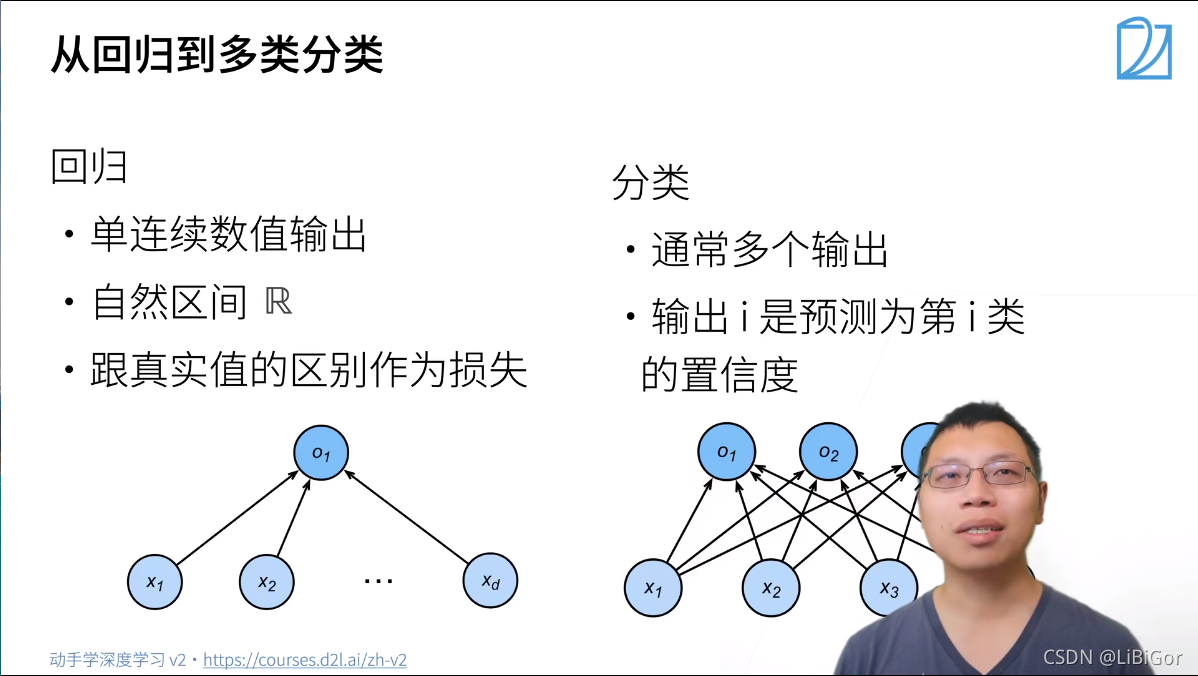
接下来,我们要选择如何表示标签。 我们有两个明显的选择:最直接的想法是选择y∈{1,2,3}, 其中整数分别代表{狗,猫,鸡}。 这是在计算机上存储此类信息的有效方法。 如果类别间有一些自然顺序, 比如说我们试图预测{婴儿,儿童,青少年,青年人,中年人,老年人}, 那么将这个问题转变为回归问题,并且保留这种格式是有意义的。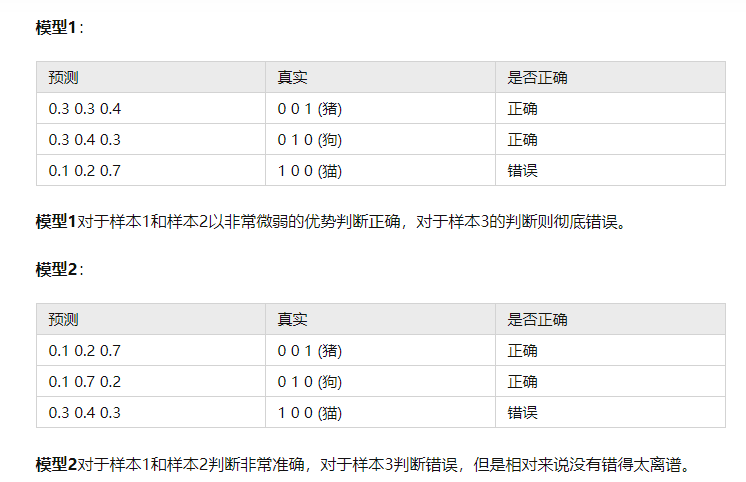
幸运的是,一般的分类问题并不与类别之间的自然顺序有关。 统计学家很早以前就发明了一种表示分类数据的简单方法:独热编码(one-hot encoding)。 独热编码是一个向量,它的分量和类别一样多。类别对应的分量设置为1,其他所有分量设置为0。
在我们的例子中,标签y将是一个三维向量, 其中(1,0,0)对应于“猫”、(0,1,0)对应于“鸡”、(0,0,1)对应于“狗”:
3.4.2. 网络架构
为了估计所有可能类别的条件概率,我们需要一个有多个输出的模型,每个类别对应一个输出。 为了解决线性模型的分类问题,我们需要和输出一样多的仿射函数(affine function)。 每个输出对应于它自己的仿射函数。 在我们的例子中,由于我们有4个特征和3个可能的输出类别, 我们将需要12个标量来表示权重(带下标的w), 3个标量来表示偏置(带下标的b)。 下面我们为每个输入计算三个未规范化的预测(logit):o1、o2和o3。
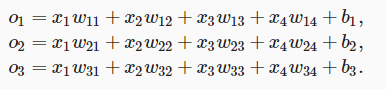
我们可以用神经网络图下来描述这个计算过程。 与线性回归一样,softmax回归也是一个单层神经网络。 由于计算每个输出o1、o2和o3取决于 所有输入x1、x2、x3和x4, 所以softmax回归的输出层也是全连接层。
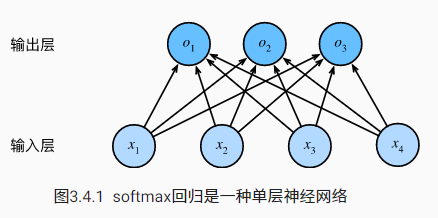
为了更简洁地表达模型,我们仍然使用线性代数符号。 通过向量形式表达为o=Wx+b, 这是一种更适合数学和编写代码的形式。 由此,我们已经将所有权重放到一个3×4矩阵中。 对于给定数据样本的特征x, 我们的输出是由权重与输入特征进行矩阵-向量乘法再加上偏置b得到的。
3.4.3. 全连接层的参数开销
正如我们将在后续章节中看到的,在深度学习中,全连接层无处不在。全连接层是“完全”连接的,可能有很多可学习的参数。 具体来说,对于任何具有d个输入和q个输出的全连接层, 参数开销为O(dq),这个数字在实践中可能高得令人望而却步。 幸运的是,将d个输入转换为q个输出的成本可以减少到O(dqn), 其中超参数n可以由我们灵活指定,以在实际应用中平衡参数节约和模型有效性。
3.4.4. softmax运算
现在我们将优化参数以最大化观测数据的概率。 为了得到预测结果,我们将设置一个阈值,如选择具有最大概率的标签。
要将输出视为概率,我们必须保证在任何数据上的输出都是非负的且总和为1。 此外,我们需要一个训练目标,来鼓励模型精准地估计概率。 在分类器输出0.5的所有样本中,我们希望这些样本有一半实际上属于预测的类。 这个属性叫做校准(calibration)。
社会科学家邓肯·卢斯于1959年在选择模型(choice model)的理论基础上发明的softmax函数正是这样做的: softmax函数将未规范化的预测变换为非负并且总和为1,同时要求模型保持可导。 我们首先对每个未规范化的预测求幂,这样可以确保输出非负。 为了确保最终输出的总和为1,我们再对每个求幂后的结果除以它们的总和。如下式:

这里,对于所有的jj总有0≤y^j≤1。 因此,y^可以视为一个正确的概率分布。 softmax运算不会改变未规范化的预测o之间的顺序,只会确定分配给每个类别的概率。 因此,在预测过程中,我们仍然可以用下式来选择最有可能的类别。
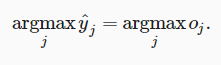
尽管softmax是一个非线性函数,但softmax回归的输出仍然由输入特征的仿射变换决定。 因此,softmax回归是一个线性模型(linear model)。
3.4.5. 小批量样本的矢量化

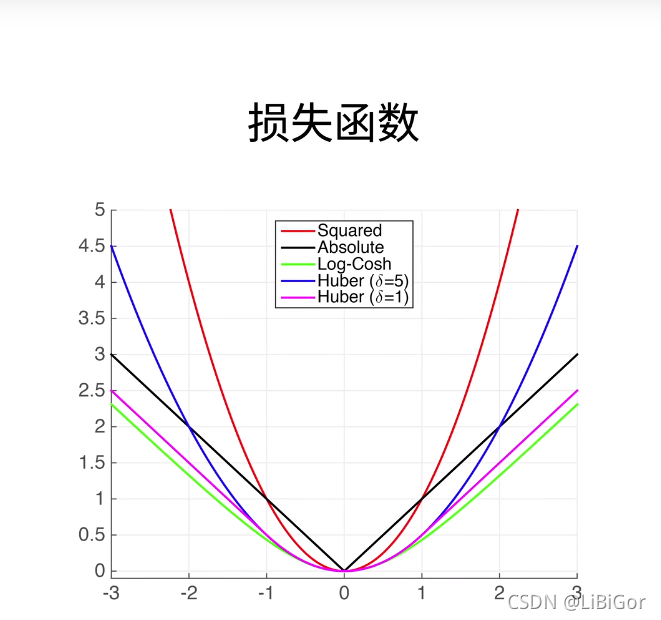
3.4.6. 损失函数
我们将使用最大似然估计来度量预测的效果。
3.4.6.1. 对数似然
 由于y是一个长度为q的独热编码向量, 所以除了一个项以外的所有项j都消失了。 由于所有y^j都是预测的概率,所以它们的对数永远不会大于0。 因此,如果正确地预测实际标签,即如果实际标签P(y∣x)=1, 则损失函数不能进一步最小化。 注意,这往往是不可能的。 例如,数据集中可能存在标签噪声(比如某些样本可能被误标), 或输入特征没有足够的信息来完美地对每一个样本分类。
由于y是一个长度为q的独热编码向量, 所以除了一个项以外的所有项j都消失了。 由于所有y^j都是预测的概率,所以它们的对数永远不会大于0。 因此,如果正确地预测实际标签,即如果实际标签P(y∣x)=1, 则损失函数不能进一步最小化。 注意,这往往是不可能的。 例如,数据集中可能存在标签噪声(比如某些样本可能被误标), 或输入特征没有足够的信息来完美地对每一个样本分类。
3.4.6.2. softmax及其导数

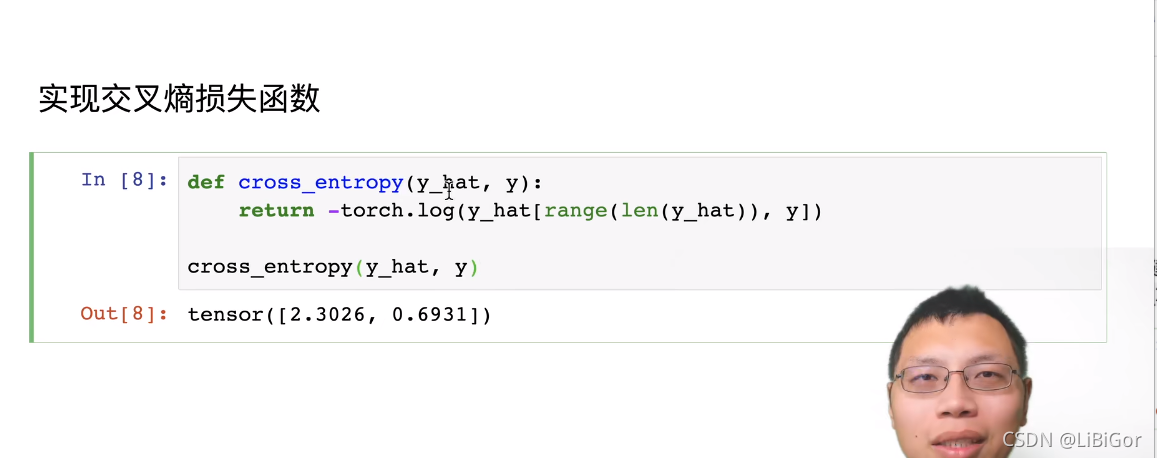
3.4.6.3. 交叉熵损失
我们观察到的不仅仅是一个结果,而是整个结果分布。 对于标签y,我们可以使用与以前相同的表示形式。 唯一的区别是,我们现在用一个概率向量表示,如(0.1,0.2,0.7), 而不是仅包含二元项的向量(0,0,1)。 我们使用 (3.4.8)来定义损失l, 它是所有标签分布的预期损失值。 此损失称为交叉熵损失(cross-entropy loss),它是分类问题最常用的损失之一。 本节我们将通过介绍信息论基础来理解交叉熵损失。 


3.4.7. 信息论基础
信息论(information theory)涉及编码、解码、发送以及尽可能简洁地处理信息或数据。
3.4.7.1. 熵
信息论的核心思想是量化数据中的信息内容,该数值被称为分布P的熵(entropy)。可以通过以下方程得到:
3.4.7.2. 惊异
压缩与预测有什么关系呢?举一个极端的例子,假如数据流中的每个数据完全相同,这会是一个非常无聊的数据流。 由于它们总是相同的,所以很容易被预测。 所以,为了传递数据流的内容,我们不必传输任何信息。 因此,当数据易于预测,也就易于压缩。
但是,如果我们不能完全预测每一个事件,那么我们有时可能会感到“惊异”。 在观察一个事件j,并赋予它(主观)概率P(j)。 当我们赋予一个事件较低的概率时,我们的惊异会更大。 在 (3.4.11)中定义的熵, 是当分配的概率真正匹配数据生成过程时的预期惊异。
3.4.7.3. 重新审视交叉熵
交叉熵想象为“主观概率为Q的观察者在看到根据概率P生成的数据时的预期惊异”。 当P=Q时,交叉熵达到最低。 在这种情况下,从P到Q的交叉熵是H(P,P)=H(P)。
简而言之,我们可以从两方面来考虑交叉熵分类目标:
(i)最大化观测数据的似然;
(ii)最小化传达标签所需的惊异。
3.4.8. 模型预测和评估
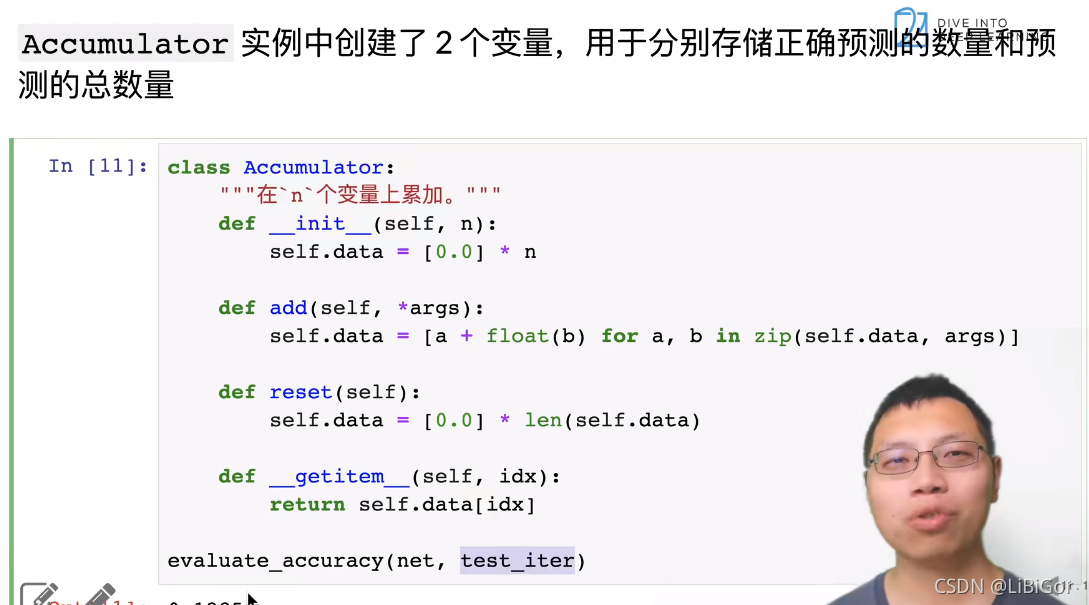
在训练softmax回归模型后,给出任何样本特征,我们可以预测每个输出类别的概率。 通常我们使用预测概率最高的类别作为输出类别。 如果预测与实际类别(标签)一致,则预测是正确的。 在接下来的实验中,我们将使用精度(accuracy)来评估模型的性能。 精度等于正确预测数与预测总数之间的比率。
3.5. 图像分类数据集
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'True' # 可能是由于是MacOS系统的原因def get_dataloader_workers():"""使用4个进程来读取数据"""return 4def load_data_fashion_mnist(batch_size, resize=None):"""下载Fashion-MNIST数据集,然后将其加载到内存中"""# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式# 并除以255使得所有像素的数值均在0到1之间trans = [transforms.ToTensor()]if resize:trans.insert(0, transforms.Resize(resize))trans = transforms.Compose(trans)mnist_train = torchvision.datasets.FashionMNIST(root="../data", train=True, transform=trans, download=True)mnist_test = torchvision.datasets.FashionMNIST(root="../data", train=False, transform=trans, download=True)return (data.DataLoader(mnist_train, batch_size, shuffle=True,num_workers=get_dataloader_workers()),data.DataLoader(mnist_test, batch_size, shuffle=False,num_workers=get_dataloader_workers()))def get_fashion_mnist_labels(labels):"""返回Fashion-MNIST数据集的文本标签"""text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat','sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']return [text_labels[int(i)] for i in labels]def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5): #@save"""绘制图像列表"""figsize = (num_cols * scale, num_rows * scale)_, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)axes = axes.flatten()for i, (ax, img) in enumerate(zip(axes, imgs)):if torch.is_tensor(img):# 图片张量ax.imshow(img.numpy())else:# PIL图片ax.imshow(img)ax.axes.get_xaxis().set_visible(False)ax.axes.get_yaxis().set_visible(False)if titles:ax.set_title(titles[i])return axes
3.6. softmax回归的从零开始实现
3.4.9. 小结¶
-
softmax运算获取一个向量并将其映射为概率。
-
softmax回归适用于分类问题,它使用了softmax运算中输出类别的概率分布。
-
交叉熵是一个衡量两个概率分布之间差异的很好的度量,它测量给定模型编码数据所需的比特数。
一、Softmax 回归
1.1视频截图

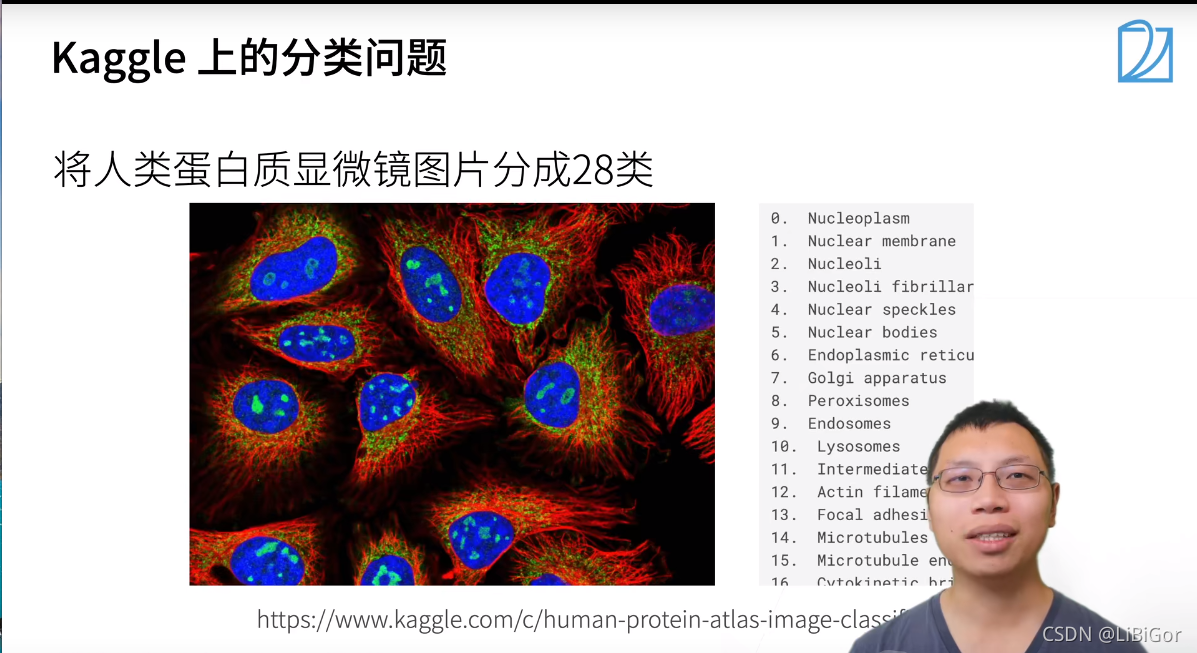
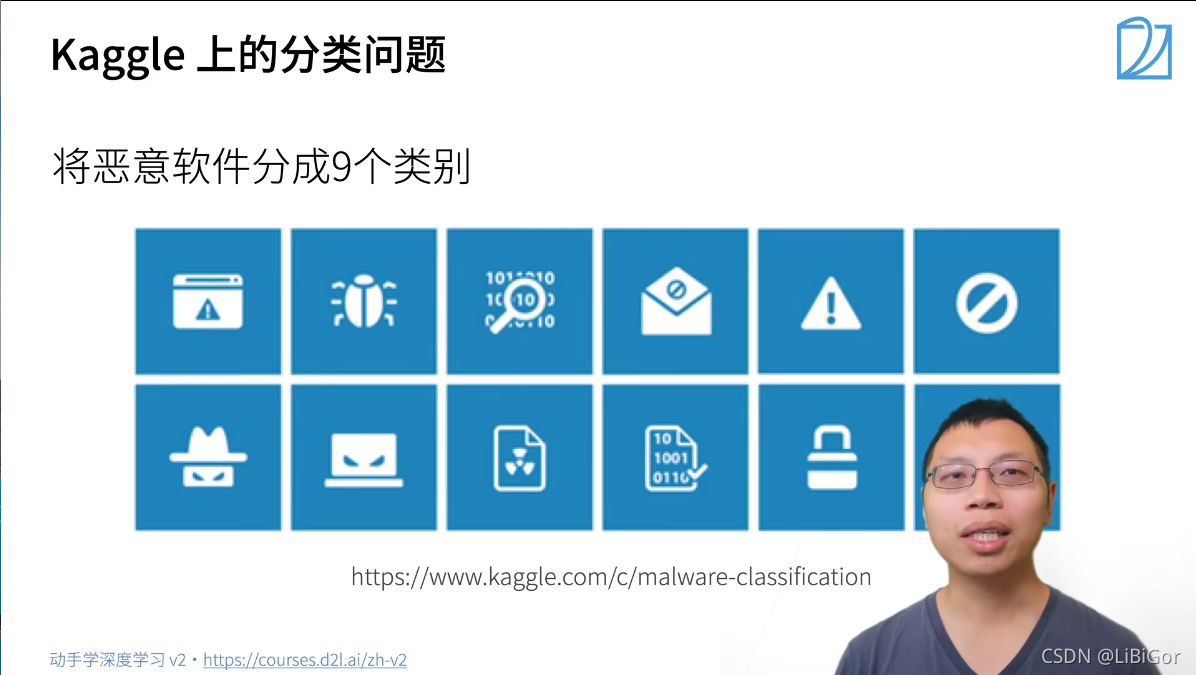

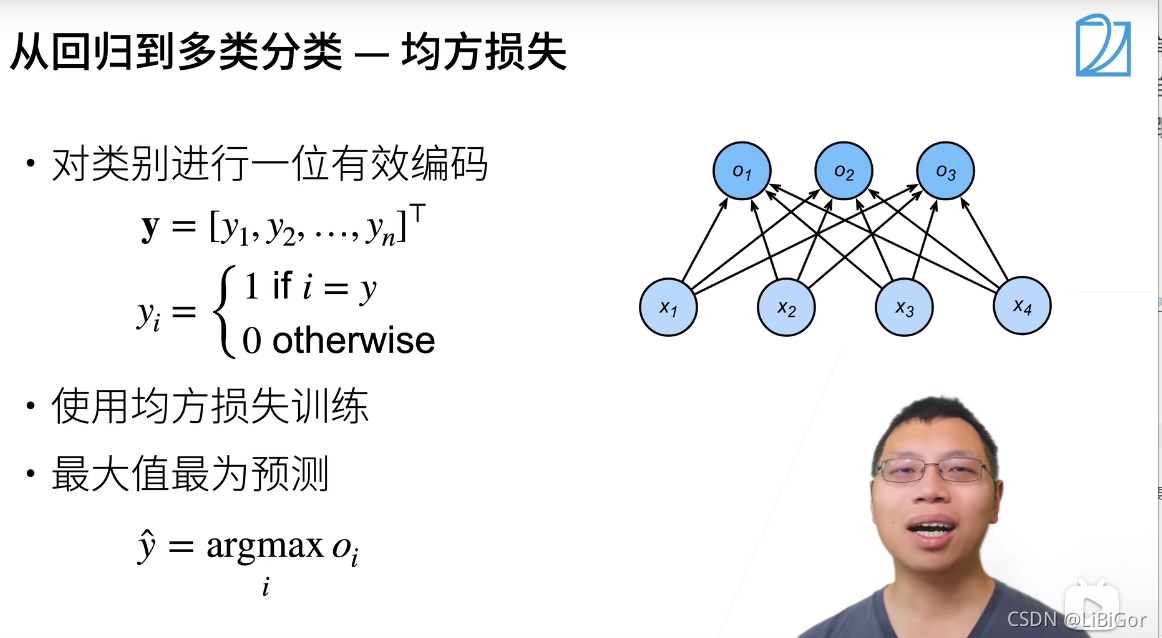
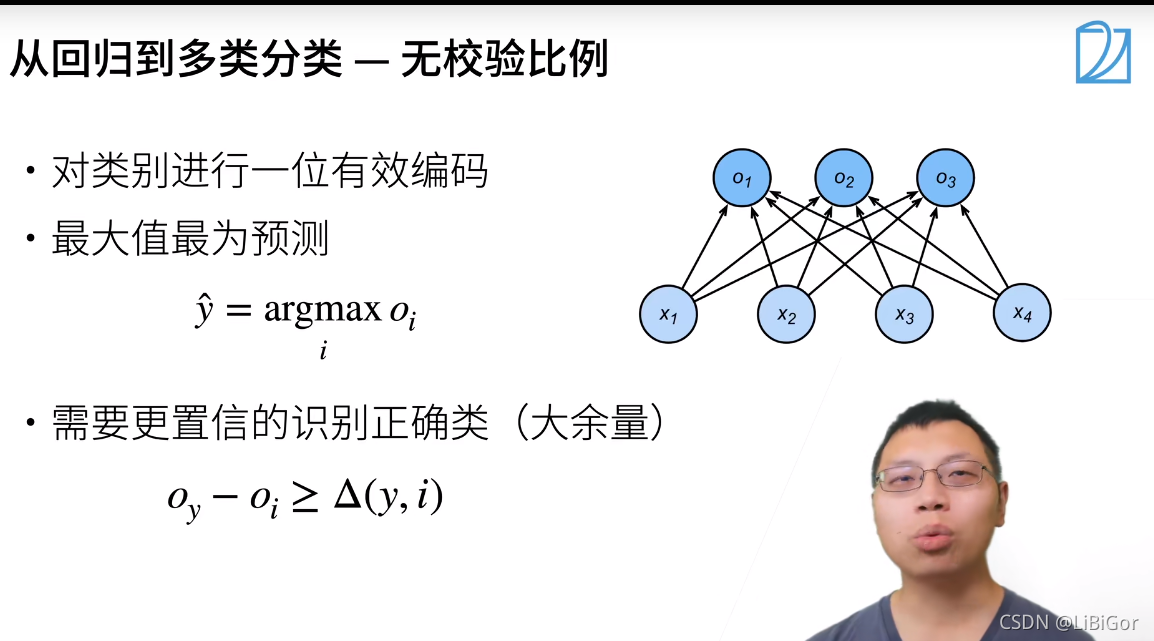
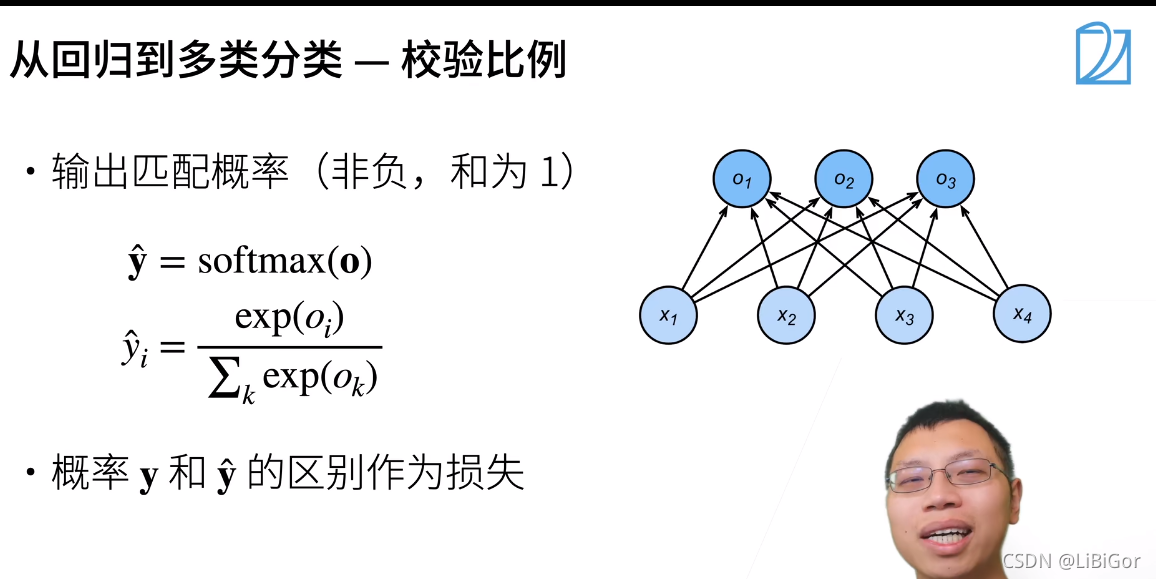


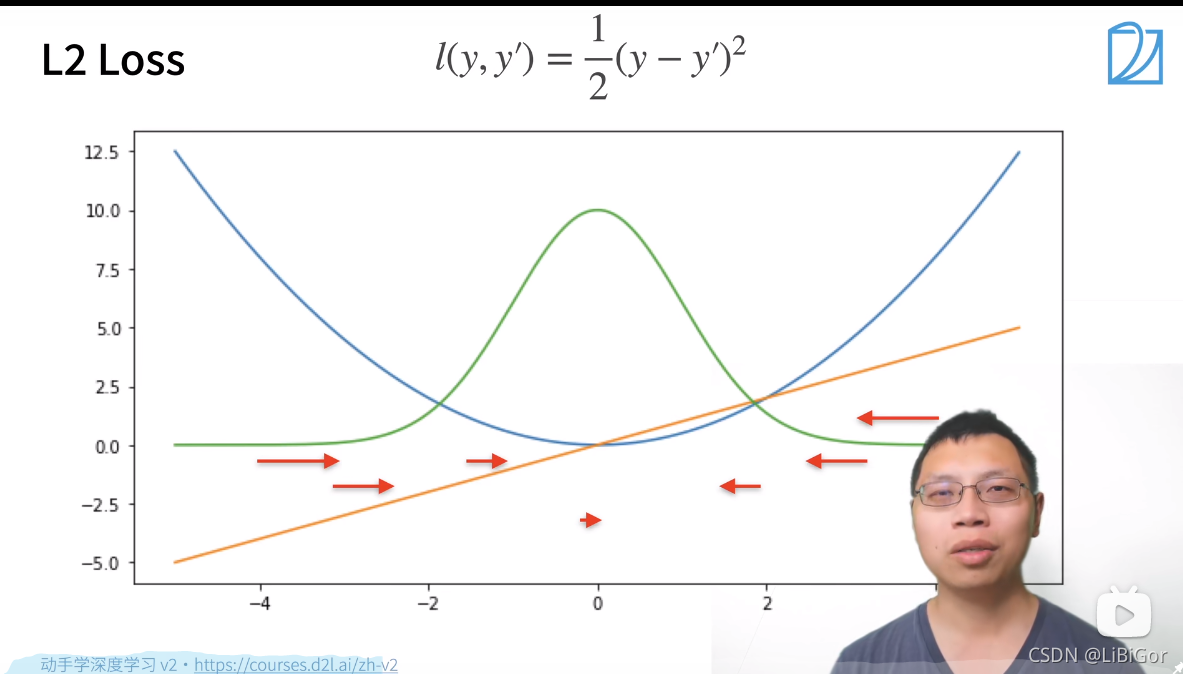
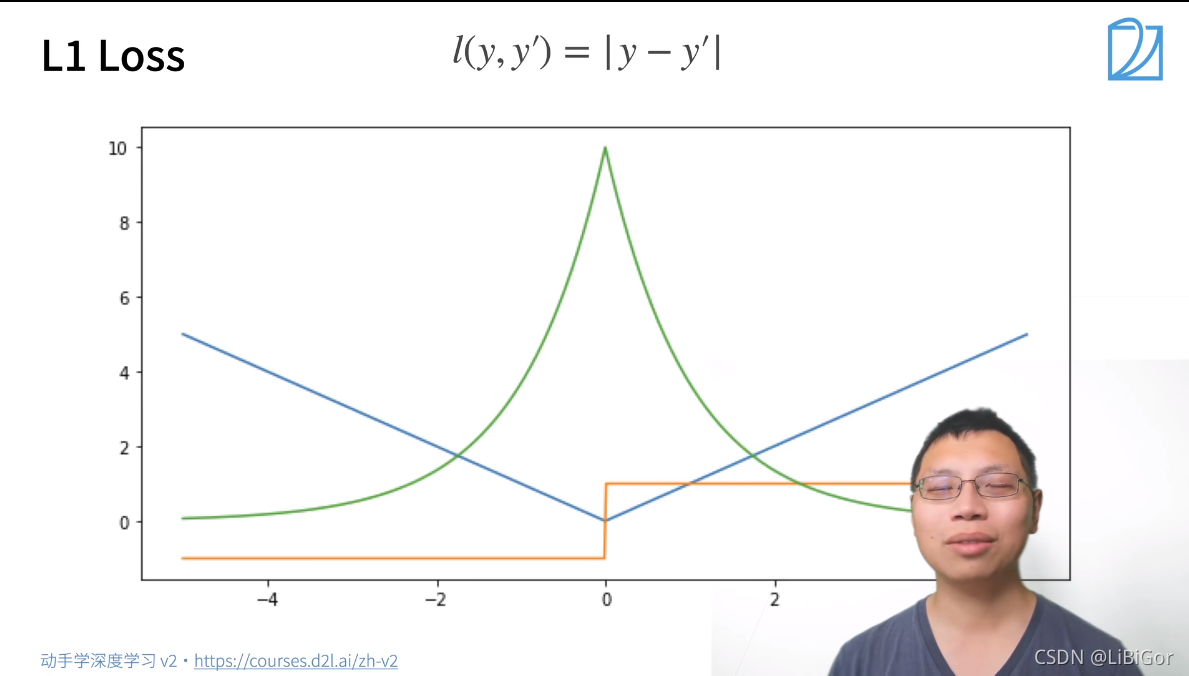
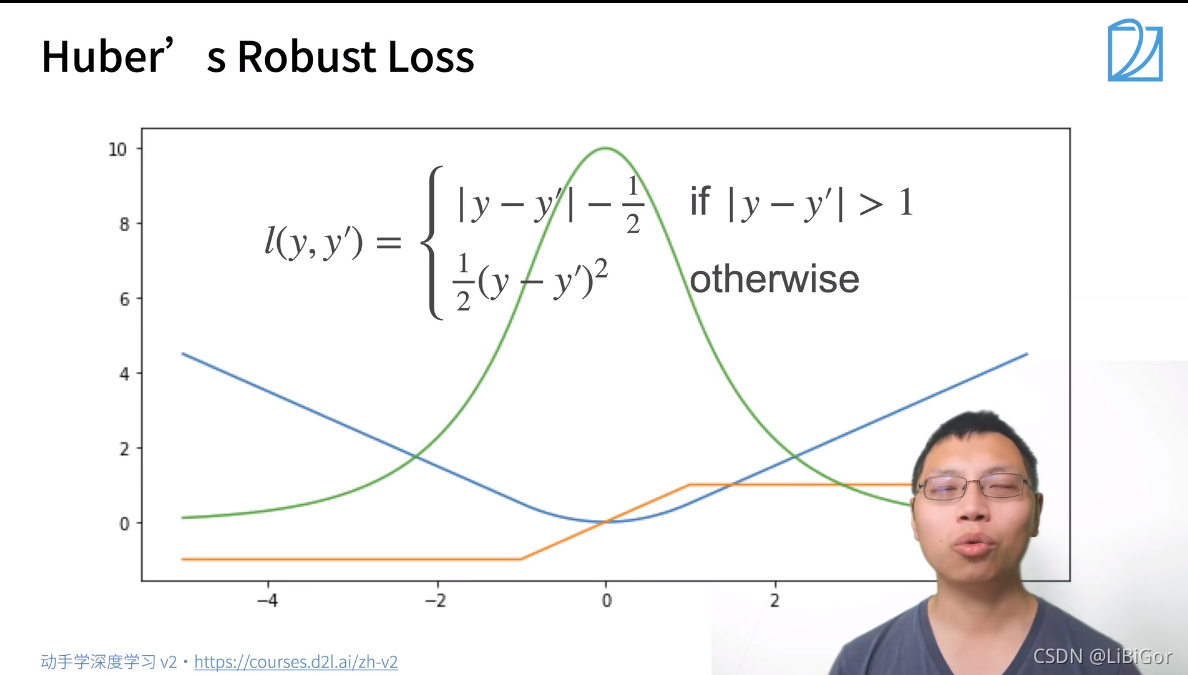
二、损失函数

三、图像分类数据集


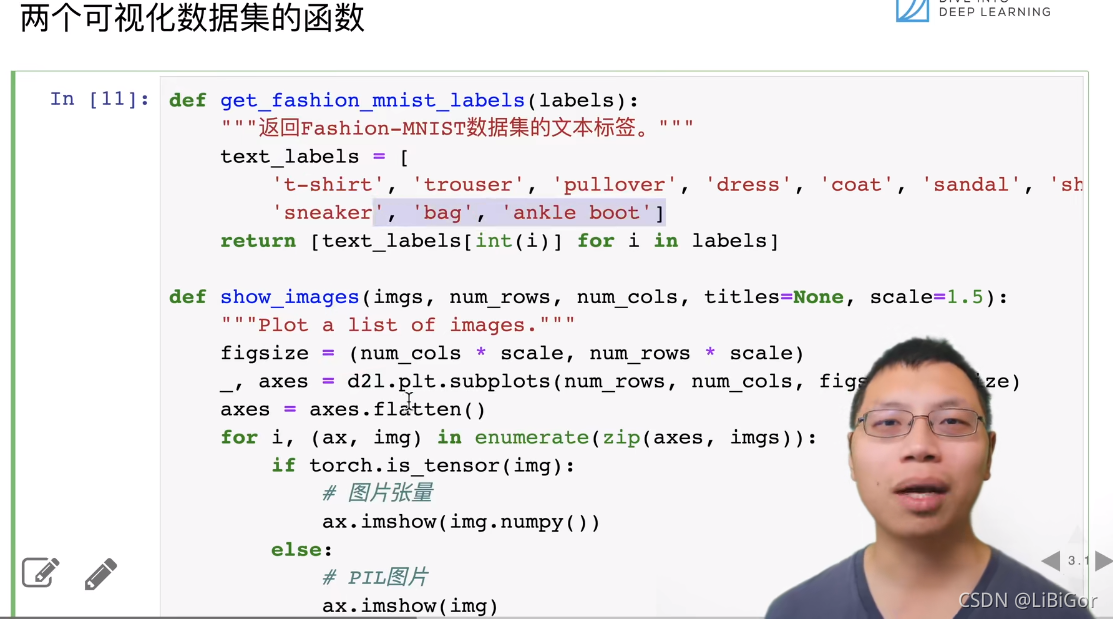
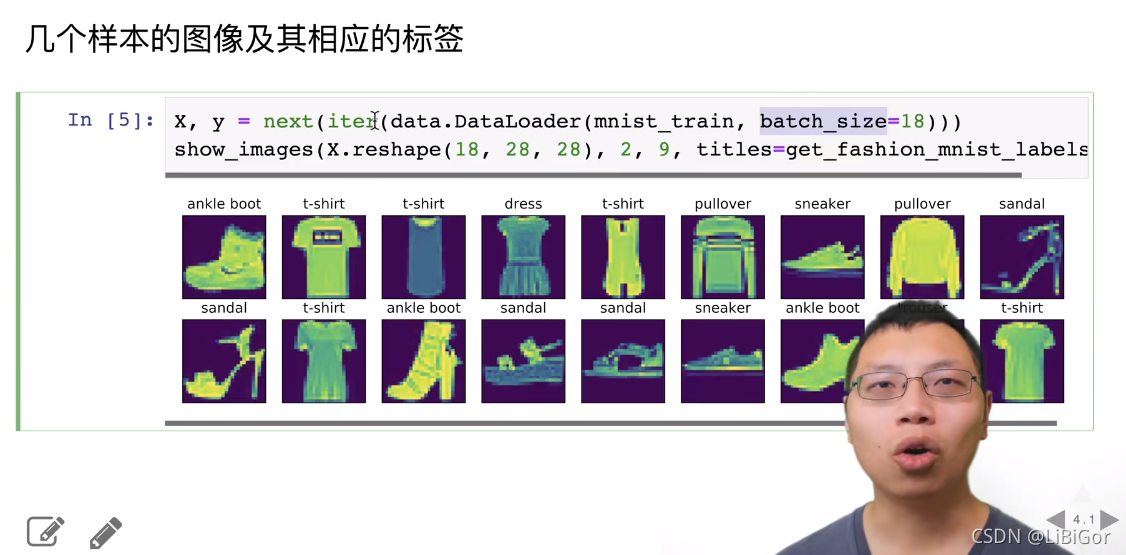

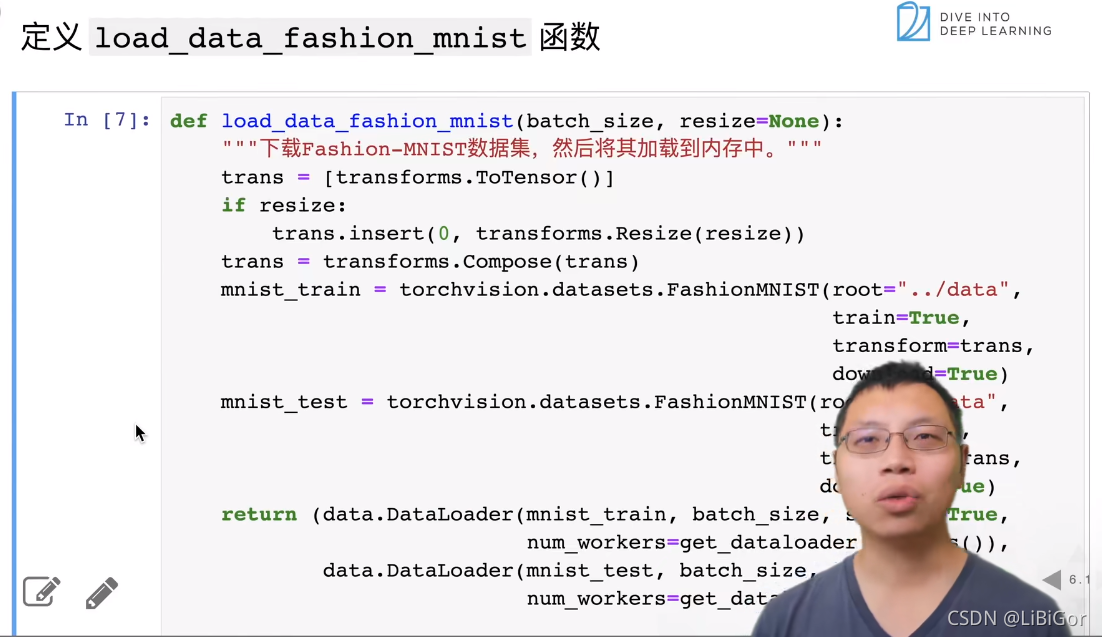
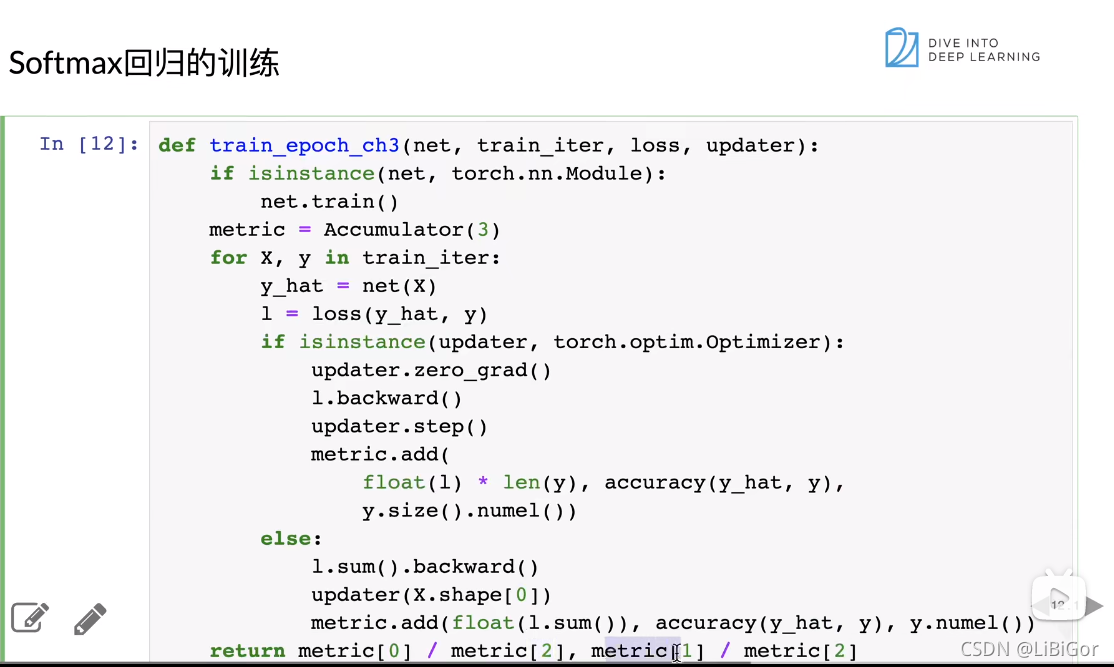
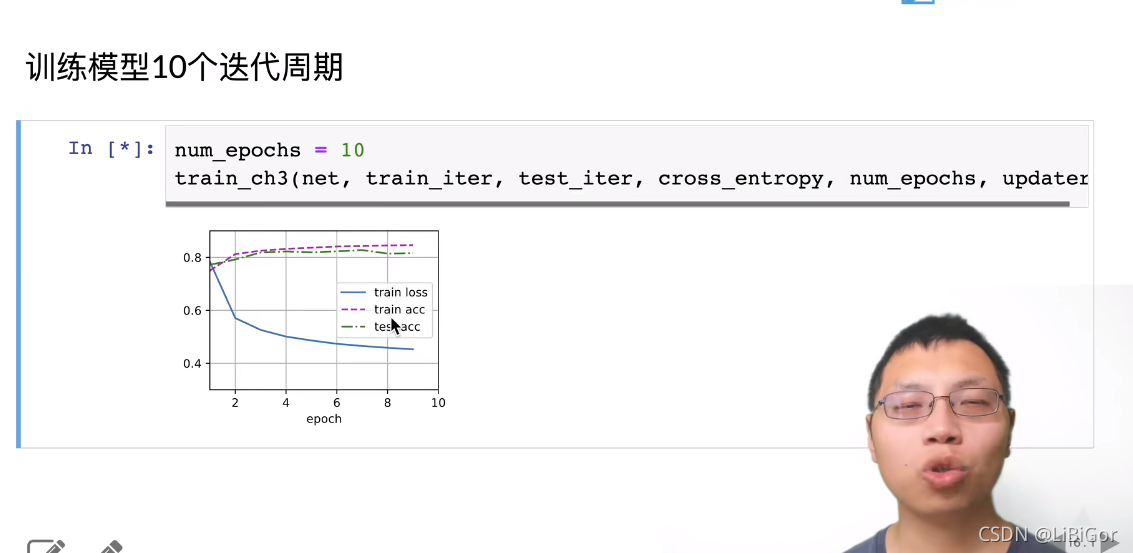
四、从0开始实现sofymax回归
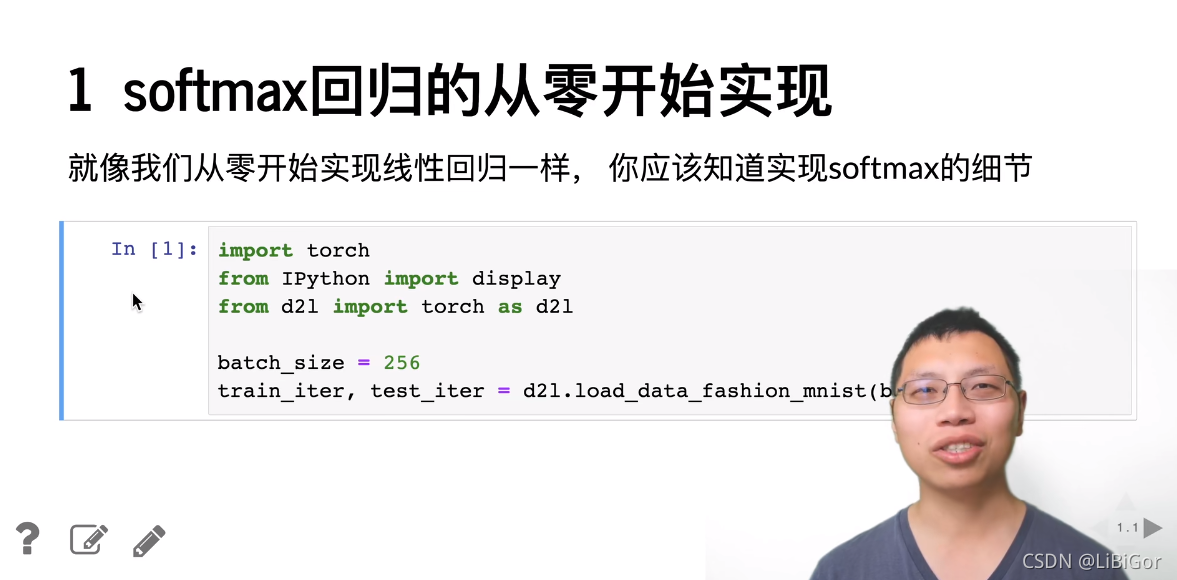
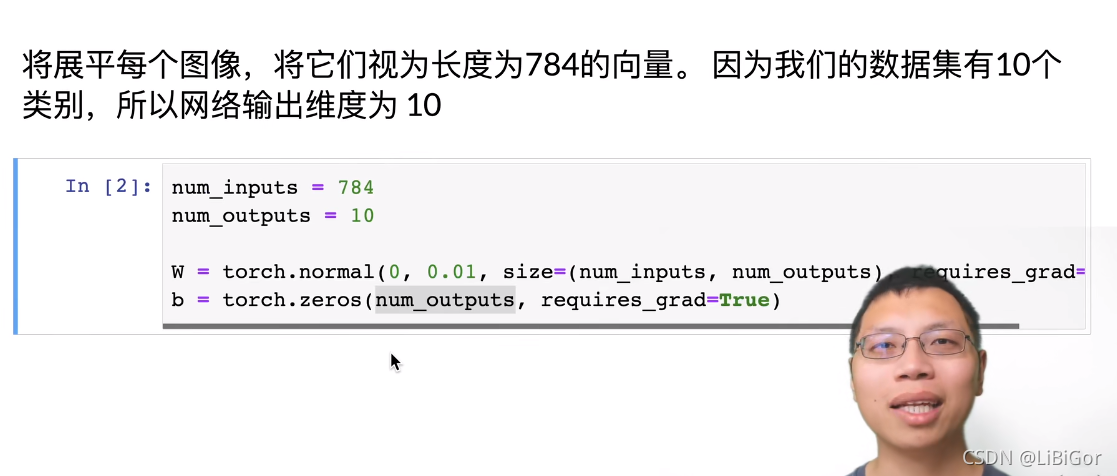










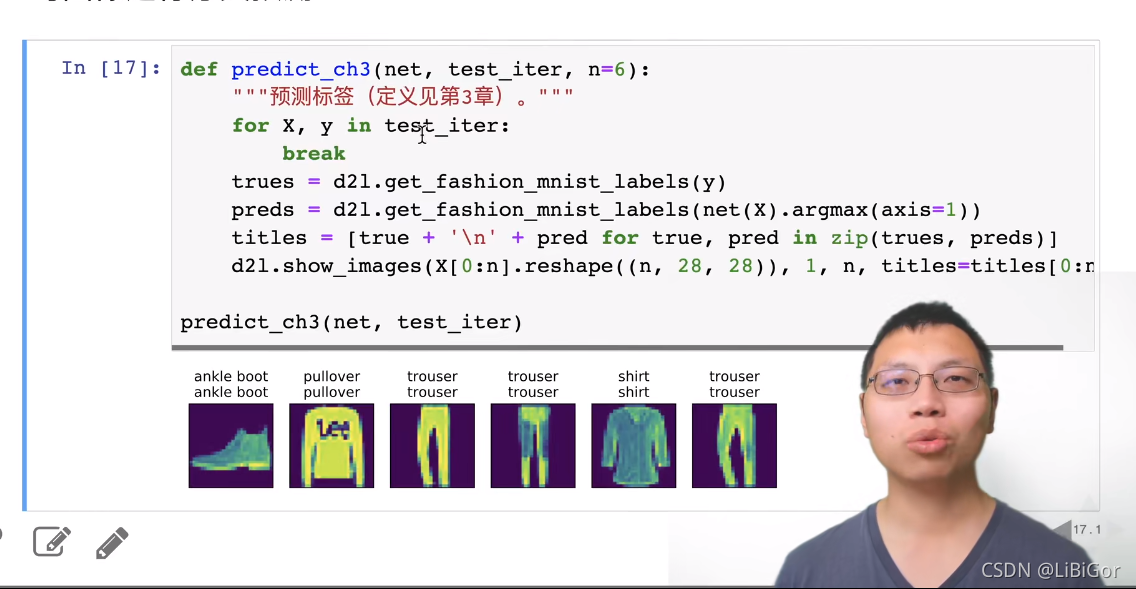
五、softmax回归的简洁实现
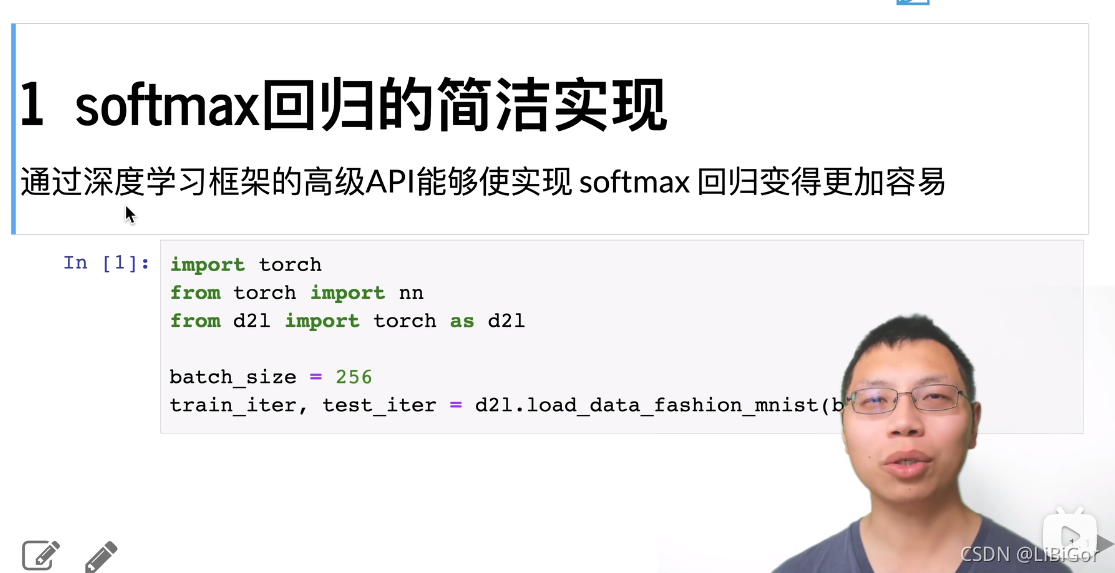


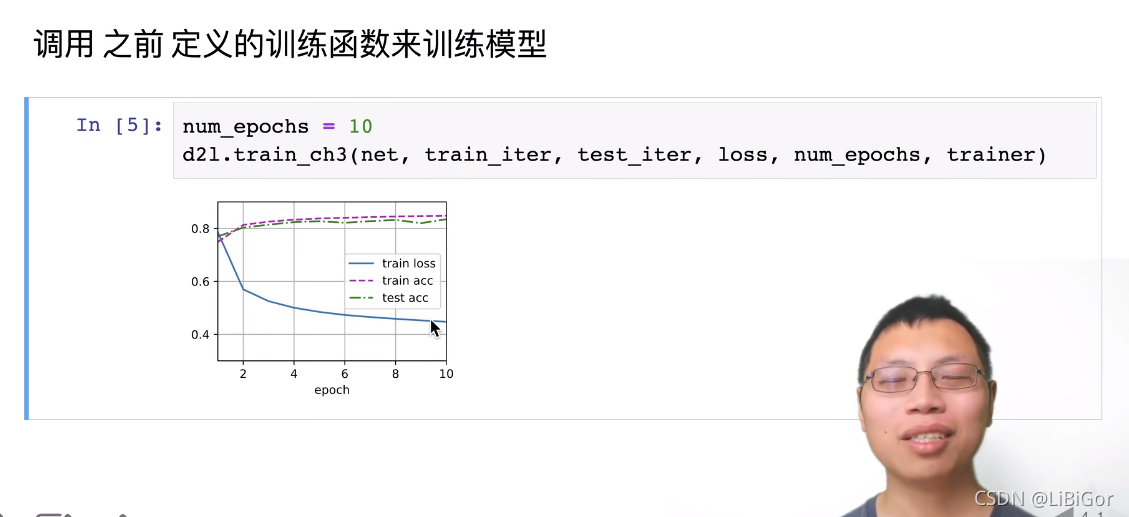
QA:
1.softmax 和 logistic类似
2.相对熵:是一个对称的关系
3.损失图中:橙色线 表示梯度的绝对值
4.最小化损失就等于最大化似然函数















)
)

渲染位图)
