我们这里对LTI系统的描述主要是用在电路分析上，我们一般先写出电路方程，对电路方程抽象以后得到微分方程

LTI系统的数学模型

这里注意一下电感上要求二阶导数，电阻上求一阶，然后为每一项分别写上系数，倘若读者到这里还没有系统的学过基尔霍夫定律，也不必纠结于这个表达式的由来。

LTI系统的框图模型

LTI系统的框图模型也是考察的重点，难度较低，但必须得掌握，例题如下：

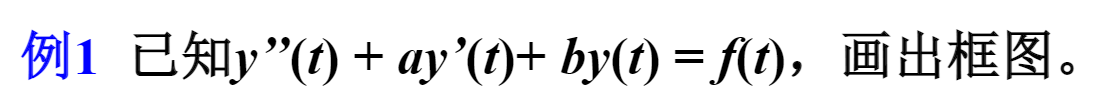
我们看到几阶导数就要有几个积分器，然后为了方便绘制，我们需要移向：

$f(t)$表示的是输入函数，输入进去后你按照阶数的高低，画两个积分器，看a，b系数的正负，如果为正，箭头方向与信号输入方向相同，反之则相反，记得按照系数的正负为每一个箭头加上正负号，为加深理解，再来一种题型

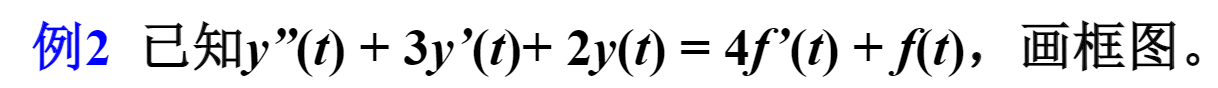
这里居然是$f(t)$与$f^{\prime }(t)$，这下又和前面说的不一样了，这下该怎么办呢？
解决方法：
我们以后看到右端若是有$f(t)$的导数，我们就可以引入辅助函数$x(t)$

详细推导展开如下：

简单的来说就是：
1.引入辅助函数$x^{\prime \prime }(t)$具体形式如图
2.右边的$f(t)$全换成$x(t)$，左边的$y(t)$全换成x(t)，化简后左边剩下一个$f(t)$，再把它换成$y(t)$
下面就到了画出信号框图的这一步：
我们前面移向的时候得到过这样一个式子：

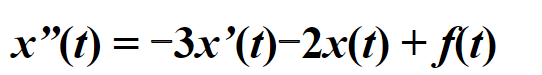
这个框图好画，现在又让咱们画题目中的框图，就是底下这个式子的框图加上题给辅助函数的框图，二者一组合


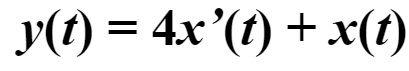
可以看到，现在我们有两个累加器了，一个是$f(t)$，一个是$y(t)$，不要忘记在靠近累加器的箭头上标注这个系数的正负号，并在箭头的连线上写上它们的系数。

现在我们会使用表达式来绘制框图了，接下来我们想一想，能不能直接从已知的框图里写出信号的表达式？答案是肯定的，只需要写出一个关于$x^{\prime \prime }(t)$的式子，一个关于$y(t)$的式子就OK了

观察后不难得出：
$x^{\prime \prime }(t)=-2x^{\prime }(t)-3x^{\prime }(t)+f(t)$ ①
$y(t)=4x^{\prime }(t)+3x(t)$ ②
然后按照前面的逆过程，对①式有
$f(t)=x^{\prime \prime }(t)+2x^{\prime }(t)+3x(t)$
$x(t)\to y(t)$
对②式有
$x(t)\to f(t)$
$y(t)=4f^{\prime }(t)+3f(t)$
联立后可以得到
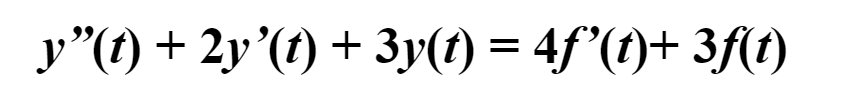