树塔狂想曲
题目大意：
有一个数字金字塔，让你求出去掉一个点后，从最顶端走到最低端的最大值（只能往下或右下走）
原题:
题目描述
相信大家都在长训班学过树塔问题，题目很简单求最大化一个三角形数塔从上往下走的路径和。走的规则是：（i，j）号点只能走向（i+1，j）或者（i+1，j+1）。如下图是一个数塔，映射到该数塔上行走的规则为：从左上角的点开始，向下走或向右下走直到最底层结束。
1
3 8
2 5 0
1 4 3 8
1 4 2 5 0
路径最大和是1+8+5+4+4 = 22，1+8+5+3+5 = 22或者1+8+0+8+5 = 22。
小S觉得这个问题so easy。于是他提高了点难度，他每次ban掉一个点（即规定哪个点不能经过），然后询问你不走该点的最大路径和。
当然他上一个询问被ban掉的点过一个询问会恢复（即每次他在原图的基础上ban掉一个点，而不是永久化的修改）。
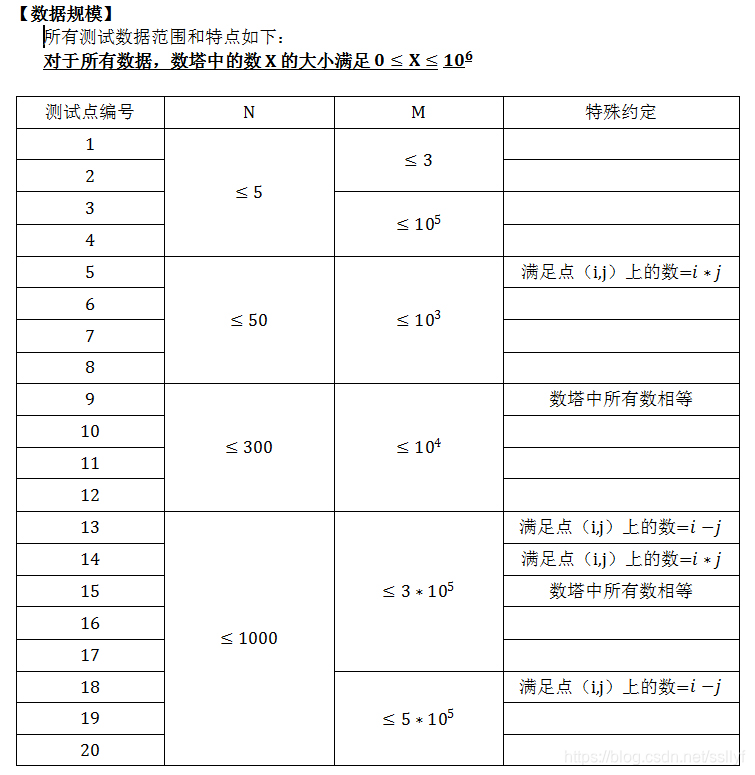
输入
第一行包括两个正整数，N，M，分别表示数塔的高和询问次数。
以下N行，第i行包括用空格隔开的i - 1个数，描述一个高为N的数塔。
而后M行，每行包括两个数X，Y，表示第X行第Y列的数塔上的点被小S ban掉，无法通行。
（由于读入数据较大，c或c++请使用较为快速的读入方式）
输出
M行每行包括一个非负整数，表示在原图的基础上ban掉一个点后的最大路径和，如果被ban掉后不存在任意一条路径，则输出-1。
输入样例
5 3
1
3 8
2 5 0
1 4 3 8
1 4 2 5 0
2 2
5 4
1 1
输出样例
17
22
-1
说明
【样例解释】
第一次是
1
3 X
2 5 0
1 4 3 8
1 4 2 5 0
1+3+5+4+4 = 17 或者 1+3+5+3+5=17
第二次：
1
3 8
2 5 0
1 4 3 8
1 4 2 X 0
1+8+5+4+4 = 22
第三次：你们都懂的！无法通行，-1！
解题思路：
很明显， 直接暴力是不可能的，我们先预处理出来从起点到某个点的最大值，和从某个点到终点的最大值，然后就可以求出经过某个点的最大值，然后就可以求出某一行的最大值和次大值
然后入过经过输入的点是最大值，那说明不能走，那走次大的，否则走最大的
代码：
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
int n,m,xx,yy,num,a[1005][1005],f[1005][1005];
int df[1005][1005],ff[1005][1005],ans[1005],ans1[1005];
int read()//快读
{char x=getchar();int d=1,l=0;while (x<'0'||x>'9') {if (x=='-') d=-1;x=getchar();}while (x>='0'&&x<='9') l=(l<<3)+(l<<1)+x-48,x=getchar();return l*d;
}
void writ(int c) {if (c>9) writ(c/10); putchar(c%10+48); return;}
void write(int s) {s<0?putchar(45),writ(-s):writ(s); putchar(10); return;}
int main()
{n=read();m=read();for (int i=1;i<=n;++i)for (int j=1;j<=i;++j){a[i][j]=read();f[i][j]=max(f[i-1][j],f[i-1][j-1])+a[i][j];//预处理}for (int i=n;i>0;--i)for (int j=1;j<=i;++j)df[i][j]=max(df[i+1][j],df[i+1][j+1])+a[i][j];for (int i=1;i<=n;++i){for (int j=1;j<=i;++j){ff[i][j]=max(f[i-1][j],f[i-1][j-1])+max(df[i+1][j],df[i+1][j+1])+a[i][j];//计算if (ff[i][j]>ans[i]) ans[i]=ff[i][j],num=j;//求最大的}for (int j=1;j<=i;++j)if (j!=num)ans1[i]=max(ans1[i],ff[i][j]);//求次大的}for (int i=1;i<=m;++i){xx=read();yy=read();if (xx==1&&yy==1) putchar(45),putchar(49),putchar(10);//无法到达else if (ff[xx][yy]==ans[xx]) write(ans1[xx]);//次大else write(ans[xx]);//最大}
}
