dotnet core时代,依赖注入基本已经成为标配了,这就不多说了.

前几天在做某个功能的时候遇到在Task中使用EF DbContext的问题,学艺不精的我被困扰了不短的一段时间,于是有了这个文章.

先说一下代码结构和场景.

首先有一个HouseDbContext,代码大概是下面这样:

public class HouseDbContext : DbContext{   
    public HouseDbContext(DbContextOptions<HouseDbContext> options): base(options)    {}    public DbSet<Notice> Notices { get; set; }
}

接着已经在StarUp.cs中初始化并注入了,注入代码是这样的:

services.AddDbContextPool<HouseDbContext>(options =>{options.UseLoggerFactory(loggerFactory);options.UseMySql(Configuration["MySQLString"].ToString());
});

有一个NoticeService.cs 会用到HouseDbContext 进行增删查改

当然我们也需要把NoticeService注入到容器中,类似这样

services.AddScoped<NoticeService,NoticeService>();

现在一切都是很美好的,也能正常查询出Notice

然后某一天来了,有个需求是Update Notice之后需要把Notice同步到另外一个地方,例如Elasticsearch?

代码如下:

然后一跑...

代码炸了...

恭喜你获得跨线程使用EF DbContext导致上下文不同步的异常.

错误大概长这样.

System.ObjectDisposedException: Cannot access a disposed object. A common cause of this error is disposing a context that was resolved from dependency injection and then later trying to use the same context instance elsewhere in your application. This may occur if you are calling Dispose() on the context, or wrapping the context in a using statement. If you are using dependency injection, you should let the dependency injection container take care of disposing context instances.      Object name: 'HouseDbContext'.

估计现在整个人都不好了.

这个撒意思呢?

无法访问被释放的对象。这种错误的一个常见原因是使用从依赖注入中解决的上下文，然后在应用程序的其他地方尝试使用相同的上下文实例。如果您在上下文上调用Dispose()，或者在using语句中包装上下文，可能会发生这种情况。如果使用依赖项注入，则应该让依赖项注入容器处理上下文实例。

用人话来说是什么意思呢?

这里的HouseDbContext是依赖注入进来的,生命周期由容器本身管理;

在Task.Run中再次使用HouseDbContext实例中由于已经切换了线程了,

HouseDbContext实例已经被释放掉了,无法再继续使用同一个实例,我们应该自己初始化HouseDbContext来用.

到这里的话,上次我做的时候心生一计:

既然我们不能直接从构造函数注入的HouseDbContext实例的话,我们是不是可以直接从依赖注入容器中拿一个实例回来呢?

那在dotnet core里面可以用个什么从容器中取出实例呢?

答案是:IServiceProvider

代码如下:

跑一下看看...

然而事实告诉我,实例是能拿得到,然而还是会炸,错误是一样的.

原因其实还是一样的,这里已经不受依赖注入托管了,人家的上下文你别想用了.

那咋办呢...

在EF6,还可以直接new HouseDbContext 一个字符串进去初始化,在EF Core这里,已经不能这样玩了.

那可咋办呢?

翻了好多资料都没看到有人介绍过咋办,最后居然还是在官网教程里面找到了样例.

先看代码...

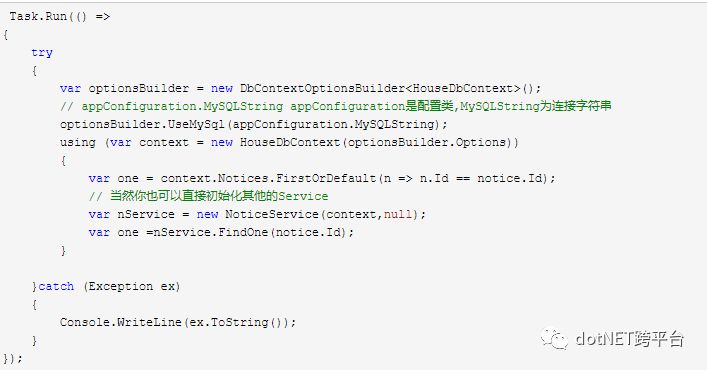
教程代码在:Configuring a DbContext： https://docs.microsoft.com/en-us/ef/core/miscellaneous/configuring-dbcontext 

大功告成...

原文地址:https://www.cnblogs.com/liguobao/p/9992451.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com