无向图割点、桥、双连通分量

• 给定无向联通图G=（V,E） • 对于一个点x，若从图中删除x及所有与x相连的边，图不再联通，x是G的割点
• 对于一条边e，从图中删去e，图不再联通，e的x的割边
• 一个图如果不存在割点，则它是一个点双连通图，一个图的极大点双连通子图是他的点双连
通分量。
• 一个图如果不存在割边，则它是一个边双连通图，一个图的极大边双连通子图是他的边双连
通分量。

Tarjan算法求割点和桥（割边）

时间戳dfn ：第n个搜到这个点
返祖边：搜索树上一个点连向其祖先节点的边
横插边：搜索树上一个点连向它另一条支链上的点的边----在无向图中不存在
追溯值low：当前点及其子树的返祖边能连到的dfn值最小的点
如果<u,v>是搜索树的边：low[u]=min(low[u],low[v])


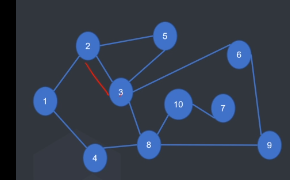
• u点是割点，v是u搜索树上的一个儿子：dfn[u] <= low[v] ——v的子树中没有返祖边能跨越u点；有多个儿子的根节点
比如图中的点10和点7

• 边是桥，搜索树上v是u的儿子：dfn[u]<low[v]——v的子树中没有返祖边能跨越<u,v>这条边

代码：

void tarjan(int x)//求割点 
{dfn[x]=low[x]=++cnt;int flag=0;for(int i=head[x];i;i=edge[i].next){int v=edge[i].v;if(!dfn[v]){tarjan(v);low[x]=min(low[x],low[v]);if(low[v]>=dfn[x]){flag++;if(x!=root||flag>1)book[x]=1;//flag>!说明根有两个以上的儿子 }}else low[x]=min(low[x],dfn[v]);} 
}

求割边：if(low[v] > dfn[x])

边双连通分量 和 点双连通分量

• 把桥删了每个连通块都是一个边双联通分量——标记出桥之后dfs一遍即可
• 点双连通分量要复杂一些——一个割点可能属于多个双联通分量

点双连通分量性质：
任意两点间至少存在两条点不重复的路径等价于图中删去任意一个点都不会改变图的连通性，即BCC中无割点
若BCC间有公共点，则公共点为原图的割点
无向连通图中割点一定属于至少两个BCC，非割点只属于一个BC

点双连通分量求法:：
• 维护一个栈
• 第一次访问某个节点时，将其入栈
• 当割点判断法则中dfn[x]<=low[y]成立时，不断从栈中弹出节点，直到y被弹出，这些被弹出的点和x一起构成一个点双连通分量

代码

#include<cstdio>
#include<cctype>
#include<vector>
using namespace std;
struct edge
{int to,pre;
}edges[1000001];
int head[1000001],dfn[1000001],dfs_clock,tot;
int num;//BCC数量 
int stack[1000001],top;//栈 
vector<int>bcc[1000001];
int tarjan(int u,int fa)
{int lowu=dfn[u]=++dfs_clock;for(int i=head[u];i;i=edges[i].pre)if(!dfn[edges[i].to]){stack[++top]=edges[i].to;//搜索到的点入栈 int lowv=tarjan(edges[i].to,u);lowu=min(lowu,lowv);if(lowv>=dfn[u])//是割点或根 {num++;while(stack[top]!=edges[i].to)//将点出栈直到目标点 bcc[num].push_back(stack[top--]);bcc[num].push_back(stack[top--]);//目标点出栈 bcc[num].push_back(u);//不要忘了将当前点存入bcc }}else if(edges[i].to!=fa)lowu=min(lowu,dfn[edges[i].to]);return lowu;
}
void add(int x,int y)//邻接表存边 
{edges[++tot].to=y;edges[tot].pre=head[x];head[x]=tot;
}
int main()
{int n,m;scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int x,y;scanf("%d%d",&x,&y);add(x,y),add(y,x);}for(int i=1;i<=n;i++)//遍历n个点tarjan if(!dfn[i]){stack[top=1]=i;tarjan(i,i);}for(int i=1;i<=num;i++){printf("BCC#%d: ",i);for(int j=0;j<bcc[i].size();j++)printf("%d ",bcc[i][j]);printf("\n");}return 0;
}

边双连通分量 和 点双连通分量 的缩点

• 每个边双连通分量缩成一个点，再用原来的桥把他们连起来
• 点双联通分量因为一个割点可能包含在多个点双连通分量里面，所以我们将每个割点保留割点与其所在的点双连通分量连边即可。

有向图的弱连通与强连通

• 在有向图G=（V，E）中，如果对于任意两点u，v，存在一条从u到v或者从v到u的路径——弱联通
• 在有向图G=（V，E）中，如果对于任意两点u，v都互相可达——强联通

强连通分量

• 有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路
径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。 • 如果有向图G的每两个顶点都强连通，称G是一个强连通图。
• 有向图的极大强连通子图，称为强连通分量(strongly connected components)。

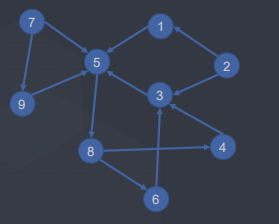
Kosaraju算法

• 对原图进行一次dfs（任意起点）
• 在第一次形成的森林的每一颗树里，以第一次搜索出栈时间的逆序对反图进行dfs，这次搜索A能到达的点和A都在一个强连通分量里面

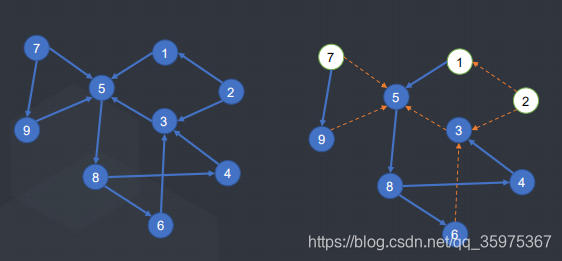
Tarjan算法

• Dfn[n]时间戳
• Low[n]他和他的子树里返祖边和横叉边能连到还没出栈的dfn最小的点
• 在dfs的时候维护一个栈第一次访问到某个点就将其加入到栈中，当一个点x的dfn[x] == low[x] 时，他就是这个强连通分量里面在搜索树中最高的点，将栈里点出栈直到x也出栈为止，这些点组成一个强连通分量。

代码：

void tarjan(int x)
{dfn[x]=low[x]=++cnt;stack[++top]=x;vis[x]=1;//x是否在栈里 for(int i=head[x];i;i=edge[i].next){int v=edge[i].v;if(!dfn[v]){tarjan(v);low[x]=min(low[x],low[y]);}else if(vis[v])low[x]=min(low[x],dfn[v]);if(dfn[x]==low[x])//是否是强连通分量最高的点 {ans++;//新强连通的标号 do{int cur=stack[top--];//栈顶的点 vis[cur]=false;num[cur]=ans;}while(x!=cur);}}}