结构体概念

在实际问题中，一组数据往往具有不同的数据类型。
例如：人口大普查时，需要记录每一个人的姓名，年龄，性别，身份证等
这些信息分别要用整型，字符型，字符串型来记录。
为了解决这种问题，C++语言给出了另一个构造数据类型——“结构体”，
它在数据存储方面相当于其他高级语言的记录，但它有这面向对象的优势

定义结构体

定义结构体及结构体变量

有两种形式：
1：

struct　结构体类型名 　//struct是关键字
　　成员表；　//可以有多个成员
　　成员函数；　//可以有多个成员函数，也可以没有
}结构体变量表；　//可以同时定义多个，用“，”隔开

举个栗子

struct node {　//定义了一个名叫node的struct类型string name;int math, chinese;int total;
}a[150];//定义了a数组变量

２：

struct　结构体类型名{
　　成员表；
　　成员函数；
}；
结构体名　结构体变量名

举个栗子：

struct node {string name;int math, chinese;int total;
};
node a[150];

在定义结构体时注意，结构体变量名和结构体名不能相同。在定义结构体时，系统对其不分配实际内存，只有在定义结构体变量时，系统才为其分配内存

结构体变量的特点

（１）结构体变量可以整体操作，例如：

swap ( a[i], a[i + 1] );　　//两个结构体变量里面的所有变量都进行交换

（２）结构体变量的成员访问也很方便清晰

cin >> a[i].name;

（３）结构体变量的初始化和数组的初始化类似

node opt = { "xiaoming", 12, 34, 1243 }; 

成员调用

结构体变量和各个成员之间的引用的一般形式为：

结构体变量．成员名

我们还可以这样操作

cin >> a[i].name  //一般情况下不能写成cin>>a[i]; 
a[i].total = a[i].math + a[i].chinese;

实际上结构体成员的操作与该成员类型所具有的操作是一致的
成员运算符“．”在存取成员数值时使用其优先级最高，并且具有左结合性
在处理结构体包含结构体的时候，可写作

strua．strub．memb

表示结构体变量strua有结构体成员strub；结构体变量strub有成员memb

成员函数调用

结构体成员函数调用的一般形式为：

结构体变量．成员函数

结构体成员函数默认将结构体变量作为应用参数

---

结构体的构造函数

这个才是我写这篇博客的原因

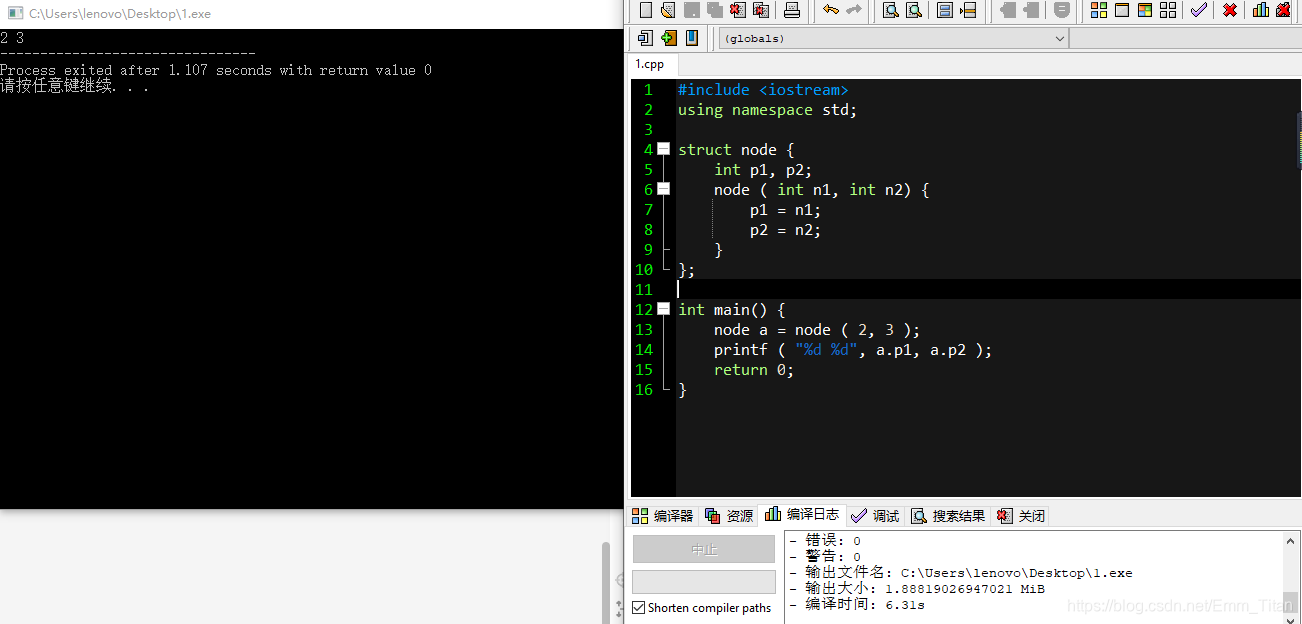
#include <iostream>
using namespace std;struct node {int p1, p2;
//这个就是构造函数了node ( int n1, int n2 ) { //可以随便取变量名，当然得是合法的p1 = n1;p2 = n2;}
};int main() {node a = node ( 2, 3 );printf ( "%d %d", a.p1, a.p2 );return 0;
}

运行结果如下，计算机自动从左到右依次匹配，把2匹配给n1,3匹配给n2

这种构造函数等同于以下多种的写法：
1.

#include <iostream>
using namespace std;struct node {int p1, p2;node ( int n1, int n2 ) :p1 ( n1 ), p2 ( n2 ) {}//构造了int类型的n1，n2，并将值赋值给了结构体里面的对应成员
};int main() {node a = node ( 2, 3 );printf ( "%d %d", a.p1, a.p2 );return 0;
}

#include <iostream>
using namespace std;struct node {int p1, p2;node ( int n1, int n2 ) {p1 = n1;p2 = n2;}
};int main() {node a ( 2, 3 );printf ( "%d %d", a.p1, a.p2 );return 0;
}

---

但是如果写成这样，计算机是无法识别的

	node a;a = node ( 2, 3 );

---

但是我又想让计算机识别该怎么办呢？？
这个时候就需要在构造函数前面再加一句

struct node {int p1, p2;node(){}node( int n1, int n2 ) {p1 = n1, p2 = n2;}
};
node a = node( 2, 3 );

这个时候你就发现计算机正常运转了

---

---

当然构造函数里面可以多传几个，也可以选择不用传的参数，如：

---

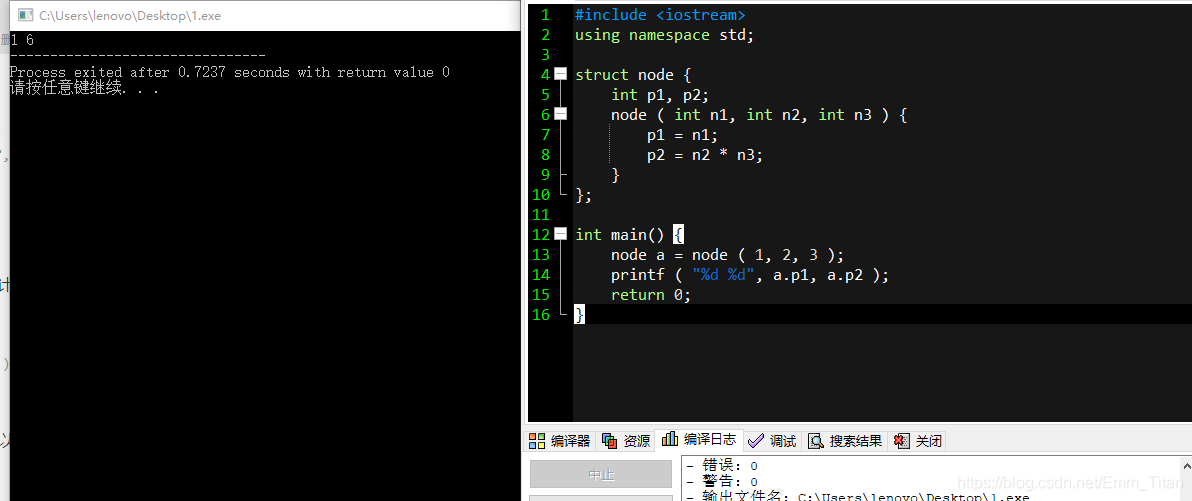
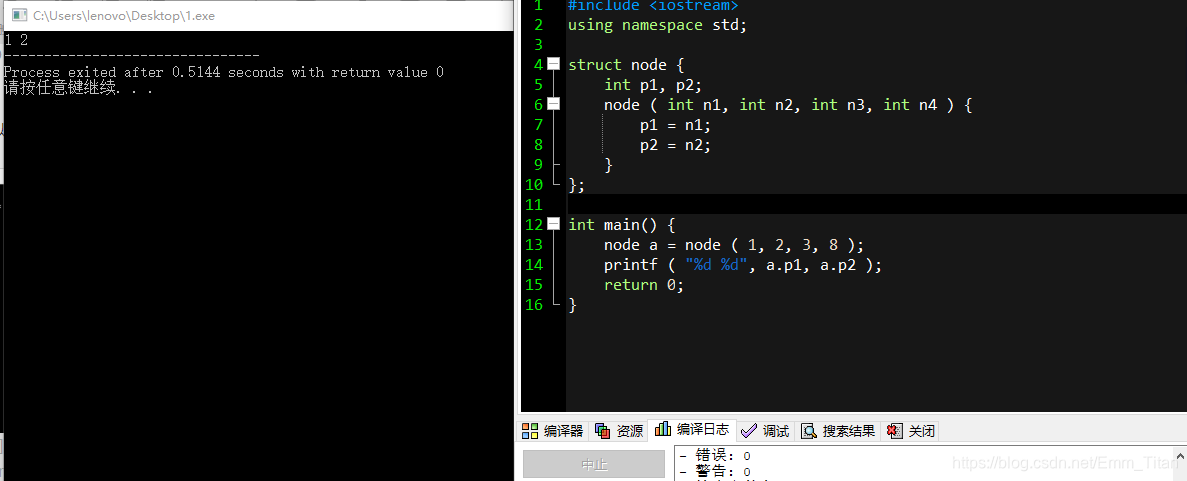
但是有可能大家会看到一些大犇将构造函数写成这样子

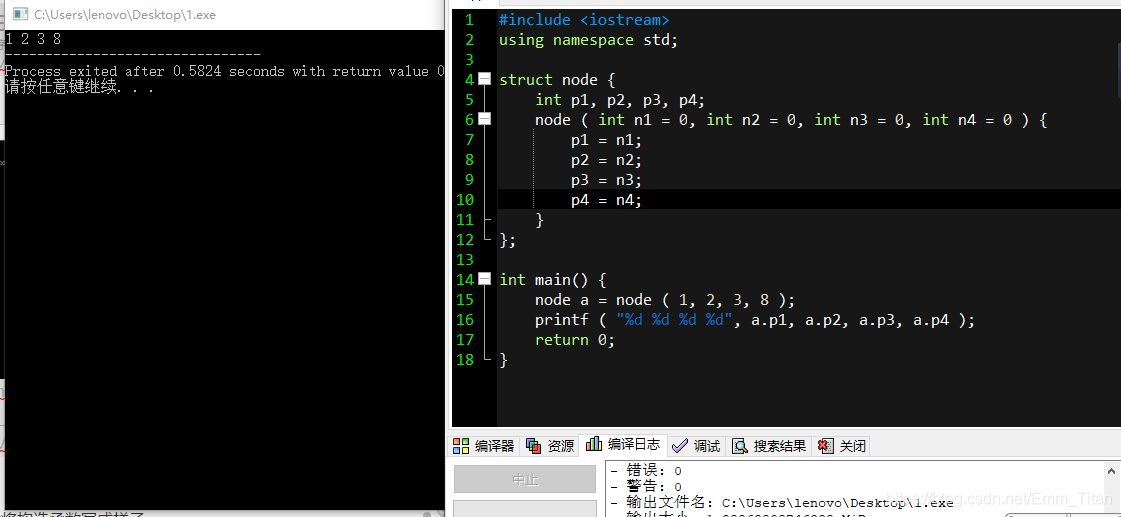
可能会疑惑为什么构造函数里面的变量定义要给赋初值呢？
可以这么想：先提前申请多个变量，后面进行构造函数传参的时候，就算我们传得不够多，也能保证每个成员是有初值的，而不是随机乱码

也可以这么理解，如果我们没有给一些成员传参赋值，那么默认成员的值就被赋值成我们定义变量的初值，如图

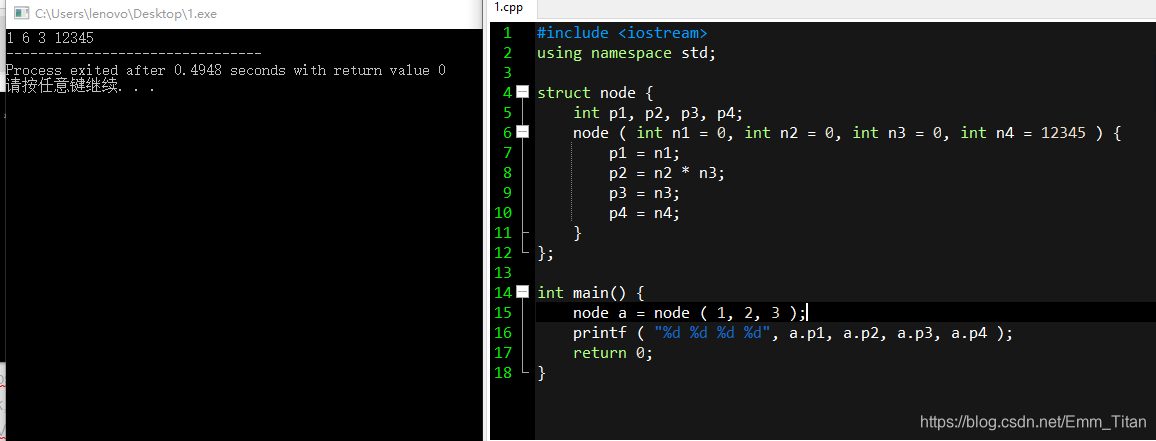
注意，因为结构体是默认从左开始匹配，所以如果少传几个参数，前面的n1,n2肯定是有值的，换言之，计算机会自动先把前面的满足了，才往后推进

---

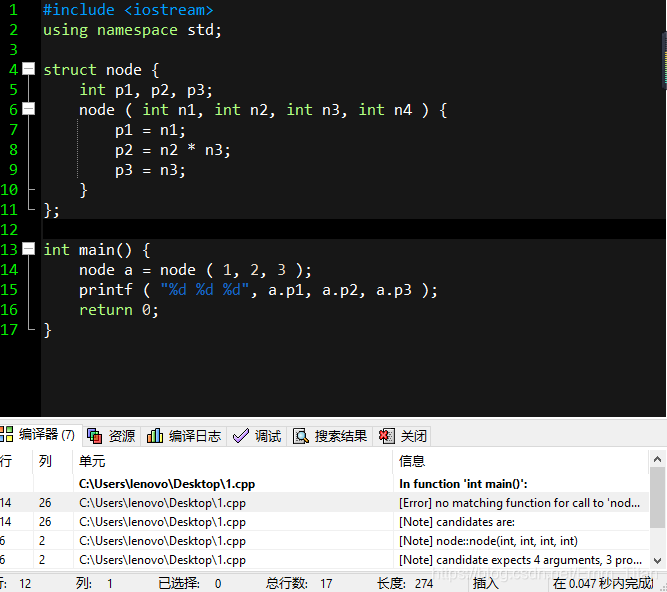
这也是为什么要赋初值的原因，如果我们不赋，后面的构造函数传参传少了，不管后面用没用到了那一个参数，就会被计算机报错，认为那是一个乱码很危险，如图

---

最后还是温馨提示，构造函数很难搞，经常容易出问题，所以大家可以采取最原始的赋值方式，尽管我喜欢构造函数

node a;
a.p1 = 2;
a.p2 = 4;
a.p3 = a.p1 * a.p2;

---

Upd1

时隔许久回来看这篇写的博客，只想由衷的感叹一句
构造函数一点都不难，只要不作死
现在基本上我的结构体构造函数已经固定写法了

struct node {int ...;node() {}node( int ... ) {}
};

如果你是一名竞赛生，不建议写各种炫技的骚操作，like this👇

struct node {int ...;node( int ... )...(), ...() {}
}

因为好像是不同的编译器标准有所出入，$C++11$下似乎可以识别，但是有些就会报错

---

建议以后写构造函数前
都加上一句

node(){}

这个语句，我自身理解为向计算机发送一种信号，告诉它我将以这种形式使用构造函数
不理解也没关系，反正多敲几个字符也少不了多少肉

加上这一句后，构造函数的两种使用
计算机都能识别成为同一个意思语句

struct node {int p1, p2;node(){}node( int n1, int n2 ) {p1 = n1, p2 = n2;}
};
node a = node( 2, 3 );
node a = { node } ( 2, 3 );

但如果不加，就只能使用原配

struct node {int p1, p2;node( int n1, int n2 ) {p1 = n1, p2 = n2;} 
}
node a = { node } ( 2, 3 );

老实说，如果不加这一句，后面的构造函数可有可无，计算机都能识别原配写法
即这么写，照样正常运行

struct node {int p1, p2; 
}
node a = { node } ( 2, 3 );

这里就多说一说这美丽的一行代码
其实它可以不为空

struct node {int n1, n2;int a[10];node() {p1 = 2;memset( a, 0, sizeof( a ) );}node( int n1, int n2 ) {p1 = n1, p2 = n2;}
}a;

这段里面的内容意思就是
一旦你申请了一个结构体$a$，计算机自动的就完成了$a.p1=2$的赋值以及结构体嵌套数组的清零操作，不用自己在里面手打一个$clear$函数就能起到同样的效果
经常在矩阵快速幂等各种场合的时候使用

Upd2

再提一句，构造函数的原配法则

上面的写法是

struct node {int a, b;
};
node x = { node } ( 2, 3 );

实际上，还可以更“原配”

struct node {int a, b;
};
node x = { 2, 3 };

对，没错，直接用大括号把赋的值包起来，连结构体名都不用写了

但是像这种计算机默认的写法，肯定是有自己铁一样的规矩的

——一定是按顺序依次赋值

也就是说，在结构体里面定义变量的顺序是，a，然后b

那么后面赋值的顺序，也一定是a=2,b=3

就不能像自己重载构造函数那么随意

struct node {int a, b;node(){}node( int A, int B ) { b = A, a = B; }
};
node x = node( 2, 3 );

这里更新主要是想说，原配也有传参数量不够的情况

struct node {int a, b, c, d;
};
node x = { 2, 3 };

这样还是a=2,b=3，但是c,d就不知道咯

Upd3

还有在初始化/初定义一个结构体的时候，连=都不要

node x( 2, 3 );

但这种写法必须建立在重载构造函数的基础上，计算机的原配是不会认识的

struct node {int a, b;node(){}node( int A, int B ) { a = A, b = B; }
};
node x( 2, 3 )

最后，现在官方都开c++14了，老实说，博主自己的构造函数都越写越简单了

私以为，没必要再像以前小心翼翼，但当然求稳肯定不是劣策