T1：分数转换

题目

Time limit: 1.5 seconds
Memory limit: 512 megabytes

给定一个十进制小数，请你将它转换为分数。
给定的小数可能有循环节，用 [] 表示，如 0.12[3] 表示 0.1233333…

Input
输入文件包含多组测试数据。
第一行一个整数 T (1 ≤ T ≤ 3 · 10⁵ )，表示测试数据的组数。
每组测试数据一行一个字符串 s i ，表示需要转换的小数，保证 1 ≤ |s i | ≤ 18，且保证由符号部分，整数
部分、小数点、小数部分组成，整数部分没有前导零，如果小数部分有循环节，则循环节一定在末尾且
循环节的最后一位非零。
Output
每组测试数据输出一行一个分数 p/q，其中 p, q 为整数且 q ≥ 1, gcd(p,q) = 1

Scoring
本题共有 3 个测试点
测试点 1 (30 分)：保证给定小数没有循环节
测试点 2 (30 分)：保证给定小数的整数部分为 0，且循环节是整个小数部分
测试点 3 (40 分)：无特殊限制

Example
frac.in
5
-0.0
0.[3]
1926.0[817]
1.00
-123.456
frac.out
0/1
1/3
19241557/9990
1/1
-15432/125

题解

旁边的dalao都说这是一道小学奥数题。。。

而我则是在考场上用尽了计算机，看了多少数据，才发现了规律

简略题解如下：
对于测试点 1，直接写成 p/10^k 后约分即可
对于测试点 2，假设循环节为 t，长度为 k，则可以列出方程 10^kx = x + t，解出来即可
对于测试点 3，只需在测试点 2 的基础上多一些细节处理

---

接下来，就让大家一起来找规律吧！！！

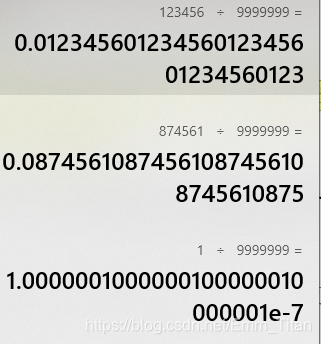
可以多打几组表看看，会发现规律如下
循环节其实就是分子（舍掉前导零），而循环节的个数就对应分母的9的个数

---

这个规律发现后，整道题就变成了一个水题
1.首先对于没有循环节的输入，如

123.1025

大家肯定都知道，将其转化为$1231025/10000$，然后在用gcd去约分化到最简即可，不再过多赘述

---

2.只有整数和循环节的输入，如

123.[7851]

就先把循环小数通过上面的规律化成分数$7851/9999$，在把整数与之同分再化简，也是gcd去完成

---

.3.整数，小数，循环节都有的输入，如样例

1926.0[817]

就先把整数与小数进行合并同分再化简，这样就又转换成了情况2，同样的处理即可

也就是说，先把输入处理成$(19260+[817])/10$，再变成了$(19260+\frac{817}{999})/10$
变成$1926+\frac{817}{9990}$再同分化简，就ok了

代码里有一些细节处理，这里就不再一一解释，大家可以自行看懂。。。

---

代码实现

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream> 
using namespace std;
#define LL long long
#define MAXN 20
int T;
char s[MAXN];LL gcd ( LL x, LL y ) {if ( ! y )return x;return gcd ( y, x % y );
}int main() {scanf ( "%d", &T );while ( T -- ) {scanf ( "%s", s );int len = strlen ( s );bool flag1 = 0, flag2 = 0;int digit = 0;LL cnt1 = 0, cnt2 = 0, cnt3 = 0;LL tot1 = 0, tot2 = 0, tot3 = 0;while ( digit < len && s[digit] == '-' ) {flag1 = 1;digit ++;}while ( digit < len && s[digit] != '.' ) {cnt1 = ( cnt1 << 3 ) + ( cnt1 << 1 ) + ( s[digit] - '0' );digit ++; tot1 ++;}if ( s[digit] == '.' )digit ++;while ( digit < len && s[digit] != '[' ) {cnt2 = ( cnt2 << 3 ) + ( cnt2 << 1 ) + ( s[digit] - '0' );digit ++;tot2 ++;}if ( s[digit] == '[' ) {digit ++;flag2 = 1;}while ( digit < len && s[digit] != ']' ) {cnt3 = ( cnt3 << 3 ) + ( cnt3 << 1 ) + ( s[digit] - '0' );digit ++;tot3 ++;}LL N = ( LL ) pow ( 10, tot2 );LL d, fenzi, fenmu;if ( tot2 != 0 ) {d = gcd ( cnt1 * N + cnt2, N );fenzi = ( cnt1 * N + cnt2 ) / d;fenmu = N / d;}else {fenzi = N;if ( cnt1 == 0 )fenzi = 0;fenmu = 1;}if ( cnt1 == 0 && cnt2 == 0 && cnt3 == 0 )flag1 = 0;if ( flag1 )printf ( "-" );if ( ! flag2 ) {printf ( "%lld/%lld\n", fenzi, fenmu );continue;}N = ( LL ) ( pow ( 10, tot3 ) ) - 1;N = N * ( LL ) ( pow ( 10, tot2 ) ); d = gcd ( cnt3, N );LL newfenzi = cnt3 / d;LL newfenmu = N / d;if ( newfenmu == fenmu ) {d = gcd ( fenzi + newfenzi, fenmu );printf ( "%lld/%lld\n", ( fenzi + newfenzi ) / d, fenmu / d );}else {d = gcd ( newfenmu, fenmu );LL lcm = newfenmu * ( fenmu / d );fenzi = fenzi * ( lcm / fenmu );newfenzi = newfenzi * ( lcm / newfenmu );d = gcd ( newfenzi + fenzi, lcm );printf ( "%lld/%lld\n", ( fenzi + newfenzi ) / d, lcm / d );}}return 0;
}

T2：Slow Path Finding Algorithm

题目

Time limit: 6 seconds
Memory limit: 512 megabytes

小 H 今天学习了「缓慢的路径寻找算法」 ，下课后便准备找一道题练习一下。题目是这样的：给定一张
有向图，每条边上都有一个小写英文字母，小 H 需要寻找一条路径使得路径上出现最多的字母的出现次
数最大。然而小 H 想了很久也只会 |V | = 1 的情形，于是他找到了你，请你帮他解决这个问题

Input
输入文件包含多组测试数据。
第一行一个整数 T (1 ≤ T ≤ 10⁵ )，表示测试数据的组数。
每组测试数据的第一行两个整数 n, m (1 ≤ n ≤ 10⁵ , 0 ≤ m ≤ 2 · 10⁵ )，分别表示有向图的点数和边数
接下来 m 行，每行两个整数 u i , v i (1 ≤ u i ,v i ≤ n) 和一个小写英文字母 c i ，表示从 u i 到 v i 有一条有向
边，上面的字母为 c i 。
保证
∑n ≤ 10 6 ,∑m ≤ 2 · 10 6 。
Output
对于每组测试数据，如果路径上出现最多的字母的出现次数可以是任意大，输出一行 -1
否则，在第一行依次输出一个整数 ans，一个字母 c 和一个整数 k (1 ≤ k ≤ n)，依次表示路径上出现最
多的字母的出现次数，达到最多出现次数的字母以及路径上的点数
第二行输出 k 个整数 p 1 ,p 2 ,…,p k (1 ≤ p i ≤ n)，表示这条路径依次经过的点
如果有多条满足条件的路径，输出任意一条

Scoring
本题共有 5 个测试点，每个测试点 20 分。
测试点 1：n,m ≤ 5。
测试点 2：每组测试数据中的 c i 均相同。
测试点 3：T,n,m ≤ 100。
测试点 4：保证图中不存在环。
测试点 5：无特殊限制。

Example
spfa.in
3
1 0
1 1
1 1 a
4 6
1 2 i
1 3 a
1 4 k
2 3 i
2 4 o
3 4 i
spfa.out
0 a 1
1
-1
3 i 4
1 2 3 4

Note
在第一组数据中，只有一个点，没有边，所以唯一的路径就是 [1]，其中每个字母的出现次数都是 0。
在第二组数据中，有一个点和它到自己的一条边，只需要选择路径 [1,1,1,…]，就能使得字母 a 出现任
意多次

题解

首先我们能知道如何判断-1的情况，如果一个字母能出现任意多次，证明有一条路可以一直重复走这一条边，那么图中肯定是有环的，所以我们可以用拓扑排序找环

---

处理了-1的情况后，再来思考对于这种树上路径求极值，很容易就想到$DP$，
设$DP[i][j]$：表示走到i号点为止，字母j出现的最多次数

而这里我们采取用父亲更新儿子节点的值，原因如下：
1.我们不知道真正的起点到底是谁，只能知道目前的终点为i
2.如果用父亲更新儿子，就可以在拓扑排序找环的时候就一起处理了

所以状态转移方程式如下：v是u的一个儿子节点，c是这条边上的字母
$$DP[v][j]=max(DP[v][j],DP[u][j]+(c==j))$$

---

最后就是路径输出问题了，其实可以在DP的时候，顺便把$DP[v][j]$状态下取最大值时所指向的父亲节点记录一下就可以了

这里在找的时候顺序会从终点找到起点，所以我们可以用stack栈来后进先出，把路径倒着输出
也可以vector存储后用一个翻转函数reverse输出也可以

代码实现

#include <queue>
#include <stack>
#include <cstdio>
#include <vector>
#include <iostream>
using namespace std; 
#define MAXN 100005
queue < int > q;
stack < int > path;
vector < vector < pair < int, int > > > G ( MAXN );
int T, n, m;
int d[MAXN];
int dp[MAXN][30], f[MAXN][30];int main() {scanf ( "%d", &T );while ( T -- ) {scanf ( "%d %d", &n, &m );for ( int i = 1;i <= n;i ++ ) {G[i].clear();d[i] = 0;for ( int j = 0;j < 26;j ++ )dp[i][j] = f[i][j] = 0;}for ( int i = 1;i <= m;i ++ ) {int u, v;char c;scanf ( "%d %d %c", &u, &v, &c );G[u].push_back( make_pair ( v, c - 'a' ) );d[v] ++;}int tot = 0;for ( int i = 1;i <= n;i ++ )if ( ! d[i] ) {q.push ( i );tot ++;}while ( ! q.empty() ) {int t = q.front();q.pop();for ( int i = 0;i < G[t].size();i ++ ) {int v = G[t][i].first;int c = G[t][i].second;for ( int j = 0;j < 26;j ++ )if ( dp[t][j] + ( c == j ) > dp[v][j] ) {dp[v][j] = dp[t][j] + ( c == j );f[v][j] = t;}d[v] --;if ( ! d[v] ) {q.push ( v );tot ++;}}}if ( tot != n )printf ( "-1\n" );else {int result = -1, str, idx;for ( int i = 1;i <= n;i ++ )for ( int j = 0;j < 26;j ++ )if ( dp[i][j] > result ) {result = dp[i][j];str = j;idx = i;}while ( idx != 0 ) {path.push ( idx );idx = f[idx][str];}printf ( "%d %c %d\n", result, str + 'a', path.size() );while ( ! path.empty() ) {printf ( "%d ", path.top() );path.pop();}printf ( "\n" );}}return 0;
}

它终于来了

T3：切面包

题目

Time limit: 1 second
Memory limit: 512 megabytes
小 H 有条一长长的面包。这条面包由 n 段组成。
每当有朋友到小 H 的家里玩，小 H 就会切下这块面包的一段，分享给朋友们。之后，小 H 又会重新制
作和之前完全一样的若干段面包填充切下的部分。
面包被切下时，有可能会裂开，第 i 段面包被切下时裂开的概率为$\frac{pi}{998244352}$ 。小 H 想让朋友尽可能开
心，于是会把裂开的面包自己吃掉，而用没有裂开的面包招待朋友。小 H 特别喜欢分块，因此，如果小
H 有 x 段连续的没有裂开的面包，则朋友的开心度为 x²
有时，小 H 也会对一段面包进行加工，加工会改变面包裂开的概率
你需要在每次小 H 切蛋糕之前，回答他朋友的期望开心度是多少

Input
第一行两个整数 n, m (1 ≤ n,m ≤ 10⁵)，分别表示面包的长度和时间的次数。
第二行 n 个整数 p 1 ,p 2 ,…,p n (0 ≤ pi ≤ 998244352)，表示每段面包初始时裂开的概率。
接下来 m 行，每行表示一个事件：
1 x i q i (1 ≤ x i ≤ n, 0 ≤ q i ≤ 998244352)——表示小 H 加工了第 x i 段面包，加工后 p[x i] 变成了 q i
2 l i r i (1 ≤ l i ≤ r i ≤ n)——表示小 H 询问若切下 [l i ,r i ] 内的面包，朋友的期望开心度是多少
Output
对每个 2 事件，输出一个整数，表示朋友的期望开心度对 998244353 取模后的值

Scoring
本题共有 5 个测试点，每个测试点 20 分
测试点 1：1 ≤ n,m ≤ 20
测试点 2：p i = 499122176，没有 1 事件
测试点 3：没有 1 事件
测试点 4：1 ≤ n,m ≤ 2 · 10³
测试点 5：无特殊限制

Example
divide.in
3 5
499122176 499122176 499122176
2 1 1
2 1 2
2 1 3
1 2 0
2 1 3
divide.out
499122177
249561089
748683266
1

Note

题解

简略题解如下：
对于测试点 1，直接枚举所有情况。时间复杂度 O(n + m2ⁿ)
对于测试点 2，答案只和长度有关，可以发现答案其实是长度的一个二次函数，直接计算即可
也可以通过递推求出。时间复杂度 O(n + m)
接下来我们需要进行一定的推导。引入辅助变量 xi，当第 i 段裂开时 xi = 1，否则 xi = 0。
连续段的数量可以看作初始的一段加上断开的连接处再减去删去的段数，即
$$1+\sum _{i=1}^{n-1}(x_i+x_{i+1}-x_i{x}_{i+1})-\sum _{i=1}^n{x}_i=1+\sum _{i=2}^{n-1}{x}_i-\sum _{i=1}^{n-1}{x}_i{x}_{i+1}$$
则段数的平方为：
$$1+\sum _{2\le i<n}\sum _{2\le j<n}{x}_i{x}_j+\sum _{1\le i<n}\sum _{1\le j<n}{x}_i{x}_{i+1}{x}_j{x}_{j+1}+2\sum _{2\le i<n}{x}_i-2\sum _{1\le i<n}{x}_i{x}_{i+1}-2\sum _{2\le i<n}\sum _{1\le j<n}{x}_i{x}_j{x}_{j+1}$$
将上式用$p_i$表示，得到：
$$1+(\sum _{i=2}^{n-1}{p}_i{)}^2+3\sum _{i=2}^{n-1}{p}_i-\sum _{i=2}^{n-1}{p}_i^2+(\sum _{i=1}^{n-1}{p}_i{p}_{i+1}{)}^2+2\sum _{i=1}^{n-2}{p}_i{p}_{i+1}{p}_{i+2}-2\sum _{i=2}^{n-2}{p}_i{p}_{i+1}^2{p}_{i+2}$$
$$-5\sum _{i=1}^{n-1}{p}_i{p}_{i+1}+2\sum _{i=2}^{n-1}{p}_i^2{p}_{i+1}+2\sum _{i=1}^{n-2}{p}_i{p}_{i+1}^2-\sum _{i=1}^{n-1}{p}_i^2{p}_{i+1}^2-2(\sum _{i=2}^{n-1}{p}_i)(\sum _{i=1}^{n-1}{p}_i{p}_{i+1})+2p_1{p}_2+2p_{n-1}{p}_n$$
对于测试点 3，直接记录前缀和即可。时间复杂度 O(n + m)
对于测试点 4，暴力查询。时间复杂度 O(nm)
对于测试点 5，使用数据结构维护 $p_i,p_i^2,p_i{p}_{i+1},p_i^2{p}_{i+1},p_i{p}_{i+1}^2,p_i^2{p}_{i+1}^2,p_i{p}_{i+1}{p}_{i+2},p_i{p}_{i+1}^2{p}_{i+2}$的和即可,时间复杂度 O(n + m lg n)。

---

接下来进入本蒟蒻的自己尽力详解版，我会尽自己的全力把这个递推式推导给大家看的

---

$$1+\sum _{i=1}^{n-1}(x_i+x_{i+1}-x_i{x}_{i+1})-\sum _{i=1}^n{x}_i=1+\sum _{i=2}^{n-1}{x}_i-\sum _{i=1}^{n-1}{x}_i{x}_{i+1}$$
首先对于这个等式，其实我们直接推右边来得更快

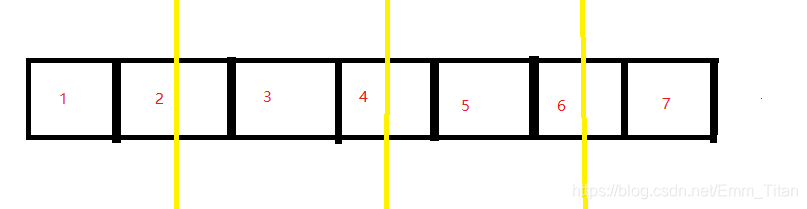
这个就是我们假设每个碎掉的面包把面包分成了多段，每两个碎掉的面包彼此之间不冲突
意思就是i面包没有和i+1面包一起碎掉，因为这样的话其实只相当于一段长度为i面包和i+1面包长度之和的面包把左右分成了两段，并非我们理想的如上图一样分成3段，i与i+1面包之前没有完整的面包
这就是$1+{\sum }_{i=2}^{n-1}{x}_i$部分

然而这只是我们的理想状态，真正是可能多个碎的面包碎在一起，形成一个更长的碎面包，这个时候分的段数就少了，1和n的端点也可能是碎的，这就是$-{\sum }_{i=1}^{n-1}{x}_i{x}_{i+1}$，为什么只有两个呢？
想一想我们把i和i+1合并成了一个大的碎面包，如果i+2面包也碎了，就再与它合并，相当于两两合并

---

关于以上公式的平方展开式，相信大家都会，我就不再赘述，进入最难环节，我们一项一项地看这个展开式是如何一步一步合并成下面那一大堆东西的

这里用$p_i$带换了$x_i$，用事件代换01，这就导致出现了下面的公式
首先要明白两个概念

$p_i\ast p_i=p_i$　　表示的意义：pi事件和pi事件同时发生的概率就是pi事件发生的概率
$p_i+p_j\ne p_i\ast p_j$ 表示的意义：pi事件发生的概率和pj事件发生的概率并不等于pi和pj事件同时发生的概率

---

①1就不变，直接往下移，好了我们已经处理好了$\frac{1}{6}$

---

②
$$+\sum _{2\le i<n}\sum _{2\le j<n}{x}_i{x}_j$$
这个如果代换成了事件p，那么这里面就一种情况是错误的，即$p_i\ast p_i=p_i$就不满足上述公式
我们得先把错误的概率减掉再加上真的概率，也就转化成了
$$+(\sum _{i=2}^{n-1}{p}_i{)}^2-\sum _{i=2}^{n-1}{p}_i^2+\sum _{i=2}^{n-1}{p}_i$$

---

③
$$+\sum _{2\le i<n}\sum _{1\le j<n}{x}_i{x}_{i+1}{x}_j{x}_{j+1}$$
与②同样的思想，这里面算错了$i=j,i=j+1,j=i+1$三种情况，在这里要明白$i=j+1,j=i+1$本质上是一致的，因为i和j只是我们的一个循环变量名罢了，我们换一下也是不会影响的，所以下面的j，我就都写成了i

对于$i=j$的情况，就得减去多算的$p_i{p}_{i+1}$；对于$i=j+1,j=i+1$的情况，得减去多算的$p_{i+1}$情况,我们就先把错误算的所有概率都减掉，再把这种情况时的正确概率加上
因为有两种，前面的系数就是2，也就转化成了
$$(\sum _{i=1}^{n-1}{p}_i{p}_{i+1}{)}^2+2\sum _{i=1}^{n-2}{p}_i{p}_{i+1}{p}_{i+2}-2\sum _{i=1}^{n-2}{p}_i{p}_{i+1}^2{p}_{i+2}-\sum _{i=1}^{n-1}{p}_i^2{p}_{i+1}^2+\sum _{i=1}^{n-1}{p}_i{p}_{i+1}$$

---

④$$+2\sum _{2\le i<n}{x}_i$$
对于这种情况舒服吧，不用变通直接转移成
$$+2\sum _{i=2}^{n-1}{p}_i$$

---

⑤$$-2\sum _{1\le i<n}{x}_i{x}_{i+1}$$
对于这种情况也是不会有冲突的，可以直接转移
$$-2\sum _{i=1}^{n-1}{p}_i{p}_{i+1}$$

---

⑥$$-2\sum _{2\le i<n}\sum _{1\le j<n}{x}_i{x}_j{x}_{j+1}$$
这里冲突的情况就是$i=j,i=j+1$，先减掉错误的概率统计，再加上正确的
由于这个式子前面的符号是$-$，我们就变成加回统计错误的部分再减掉正确的
$$-2(\sum _{i=2}^{n-1}{p}_i)(\sum _{i=1}^{n-1}{p}_i{p}_{i+1})-4\sum _{i=1}^{n-1}{p}_i{p}_{i+1}+2\sum _{i=1}^{n-1}{p}_i^2{p}_{i+1}+2\sum _{i=1}^{n-1}{p}_i{p}_{i+1}^2$$
注意观察与下列式子区别在哪里？？
$$-2(\sum _{i=2}^{n-1}{p}_i)(\sum _{i=1}^{n-1}{p}_i{p}_{i+1})-4\sum _{i=1}^{n-1}{p}_i{p}_{i+1}+2\sum _{i=2}^{n-1}{p}_i^2{p}_{i+1}+2\sum _{i=1}^{n-2}{p}_i{p}_{i+1}^2$$

区别1：
$$+2\sum _{i=1}^{n-1}{p}_i^2{p}_{i+1},+2\sum _{i=2}^{n-1}{p}_i^2{p}_{i+1}$$
发现少了一次$i=1$的值累加，那我们把它加回来
$$+2\sum _{i=1}^{n-1}{p}_i^2{p}_{i+1}=+2\sum _{i=2}^{n-1}{p}_i^2{p}_{i+1}+2p_1{p}_2$$
区别2：
$$+2\sum _{i=1}^{n-1}{p}_i{p}_{i+1}^2,+2\sum _{i=1}^{n-2}{p}_i{p}_{i+1}^2$$
发现少了一次$i=n-1$的值累加，那我们也把它加回来
$$+2\sum _{i=1}^{n-1}{p}_i{p}_{i+1}^2=+2\sum _{i=1}^{n-2}{p}_i{p}_{i+1}^2+2p_{n-1}{p}_n$$
最后我们把这种情况转移成
$$-2(\sum _{i=2}^{n-1}{p}_i)(\sum _{i=1}^{n-1}{p}_i{p}_{i+1})-4\sum _{i=1}^{n-1}{p}_i{p}_{i+1}+2\sum _{i=2}^{n-1}{p}_i^2{p}_{i+1}+2\sum _{i=1}^{n-2}{p}_i{p}_{i+1}^2+2p_1{p}_2+2p_{n-1}{p}_n$$

---

这也就是为什么我们用p代替x的时候公式里面出现了常数项的原因
最后把这拆开的六个式子合并同类项得到了上述公市

出于对代码更好操作的数据结构维护和便于合并，我们才把最后一种情况拆了一下
接下来就是如何维护八个不同的p求和，实话告诉你就是八棵线段树
但我选择了重载一次加号，一棵线段树维护八个不同的值。。。

代码实现

#include <cstdio>
#define mod 998244353
#define LL long long
#define MAXN 100005
struct node {LL p, p2, pp, p2p, pp2, p2p2, ppp, pp2p;node ( LL p = 0, LL p2 = 0, LL pp = 0, LL p2p = 0, LL pp2 = 0, LL p2p2 = 0, LL ppp = 0, LL pp2p = 0 ) :p ( p ), p2 ( p2 ), pp ( pp ), p2p ( p2p ), pp2 ( pp2 ), p2p2 ( p2p2 ), ppp ( ppp ), pp2p ( pp2p ) {} 
}tree[MAXN << 2];
int n, m;
LL p[MAXN];node operator + ( const node &u, node &v ) {return node ( ( u.p + v.p ) % mod, ( u.p2 + v.p2 ) % mod, ( u.pp + v.pp ) % mod, ( u.p2p + v.p2p ) % mod,( u.pp2 + v.pp2 ) % mod, ( u.p2p2 + v.p2p2 ) % mod,( u.ppp + v.ppp ) % mod, ( u.pp2p + v.pp2p ) % mod );
}void count ( int num, int i ) {tree[num].p = p[i] % mod;tree[num].p2 = p[i] * p[i] % mod;tree[num].pp = p[i] * p[i + 1] % mod;tree[num].p2p = tree[num].p2 * p[i + 1] % mod;tree[num].pp2 = tree[num].pp * p[i + 1] % mod;tree[num].ppp = tree[num].pp * p[i + 2] % mod;tree[num].pp2p = tree[num].pp2 * p[i + 2] % mod;tree[num].p2p2 = tree[num].pp * tree[num].pp % mod;
}void build ( int num, int l, int r ) {if ( l == r ) {count ( num, l );return;}int mid = ( l + r ) >> 1;build ( num << 1, l, mid );build ( num << 1 | 1, mid + 1, r );tree[num] = tree[num << 1] + tree[num << 1 | 1];
}void update ( int num, int l, int r, int id ) {if ( l == r ) {count ( num, id );return;}int mid = ( l + r ) >> 1;if ( id <= mid )update ( num << 1, l, mid, id );elseupdate ( num << 1 | 1, mid + 1, r, id );tree[num] = tree[num << 1] + tree[num << 1 | 1];
}node range_sum ( int num, int l, int r, int L, int R ) {if ( L <= l && r <= R )return tree[num];int mid = ( l + r ) >> 1;node lsum( 0, 0, 0, 0, 0, 0, 0, 0 ), rsum( 0, 0, 0, 0, 0, 0, 0, 0 );if ( L <= mid )lsum = range_sum ( num << 1, l, mid, L, R );if ( mid < R )rsum = range_sum ( num << 1 | 1, mid + 1, r, L, R );return lsum + rsum;
}LL query ( int l, int r ) {if ( l == r )return ( 1 - p[l] + mod ) % mod;node t = range_sum ( 1, 1, n, l, r );t.p = ( ( t.p - p[r] - p[l] ) % mod + mod ) % mod;t.p2 = ( ( t.p2 - p[r] * p[r] % mod - p[l] * p[l] % mod ) % mod + mod ) % mod;t.p2p = ( ( t.p2p - p[l] * p[l] % mod * p[l + 1] % mod- p[r] * p[r] % mod * p[r + 1] % mod ) % mod + mod ) % mod;t.pp2 = ( ( t.pp2 - p[r - 1] * p[r] % mod * p[r] % mod- p[r] * p[r + 1] % mod * p[r + 1] % mod ) % mod + mod ) % mod;t.pp = ( ( t.pp - p[r] * p[r + 1] % mod ) % mod + mod ) % mod;t.p2p2 = ( ( t.p2p2 - p[r] * p[r] % mod * p[r + 1] % mod * p[r + 1] % mod ) % mod + mod ) % mod;t.ppp = ( ( t.ppp - p[r - 1] * p[r] % mod * p[r + 1] % mod- p[r] * p[r + 1] % mod * p[r + 2] % mod ) % mod + mod ) % mod;t.pp2p = ( ( t.pp2p - p[r - 1] * p[r] % mod * p[r] % mod * p[r + 1] % mod- p[r] * p[r + 1] % mod * p[r + 1] % mod * p[r + 2] % mod ) % mod + mod ) % mod;LL ans = ( ( 1 + t.p * t.p % mod + 3 * t.p % mod - t.p2 + t.pp * t.pp % mod+ 2 * t.ppp % mod - 2 * t.pp2p % mod - 5 * t.pp % mod + 2 * t.p2p % mod + 2 * t.pp2 % mod - t.p2p2 - 2 * t.p * t.pp % mod+ 2 * p[l] * p[l + 1] % mod + 2 * p[r - 1] * p[r] % mod ) % mod + mod ) % mod;return ans;
}int main() {scanf ( "%d %d", &n, &m );for ( int i = 1;i <= n;i ++ ) {scanf ( "%lld", &p[i] );p[i] = ( mod - p[i] ) % mod; }build ( 1, 1, n );for ( int i = 1;i <= m;i ++ ) {int opt;scanf ( "%d", &opt ); if ( opt == 1 ) {int x, q;scanf ( "%d %d", &x, &q );p[x] = ( mod - q ) % mod;update( 1, 1, n, x );if ( x > 1 )update ( 1, 1, n, x - 1 );if ( x > 2 )update ( 1, 1, n, x - 2 );}else {int l, r;scanf ( "%d %d", &l, &r );printf ( "%lld\n", query ( l, r ) % mod );}} return 0;
}

如果对于推导过程有疑惑的，看不明白的，可以随时评论，也欢迎指出打错的部分，太多了，错打了几个字符很正常，谢谢