P3992 [BJOI2017]开车

题意：

题解：

我们要先将问题转换
圈是车，x是加油站。红色部分为车移动的路线
数组a是车数量的前缀和
数组b是加油站的前缀和
而a[i]与b[i]的差的绝对值就是对应的红色路被走的次数

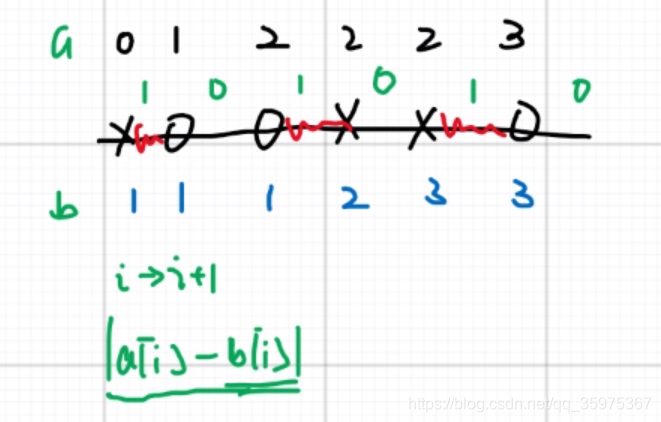
现在车发生位置移动，b数组没有影响，a数组i到j这段整体减一

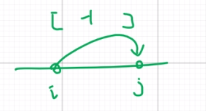
现在我们要做的就是维护a序列，支持区间+1/-1，询问∑| a[i] - b[i] |
线段树不能实现
用分块实现
实现过程：
按照下标分块，每块按照a[i] - b[i] 排序

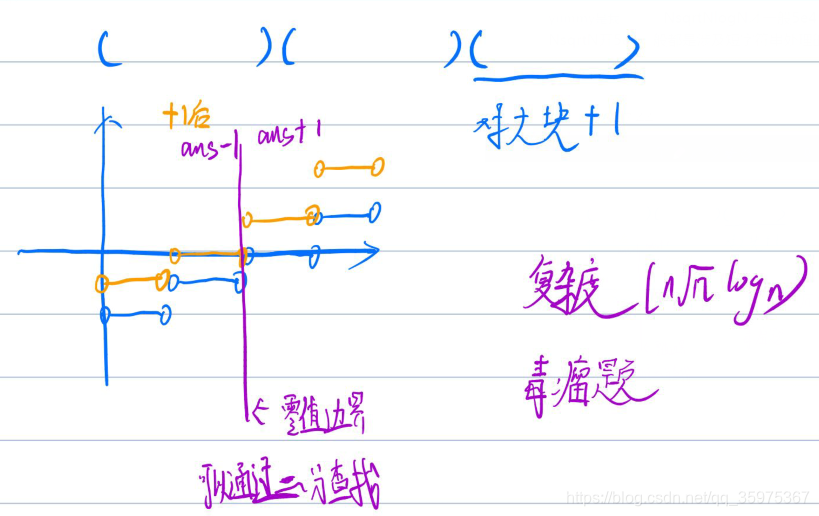
代码：

代码为借鉴

#pragma optimize("Ofast")
#include<bits/stdc++.h>
#define MAXN 150005
#define MAXB 2005
using namespace std;
typedef long long ll;int N,B,Q;
int a[MAXN], w[MAXN];
map<int,int> mp;
map<int,int>::iterator it;
map<int,int> id;int q[MAXN][2];
struct Node{int w,val,id,sw;Node(int id=0, ll val=0, int w=0):id(id), val(val), w(w){}bool operator < (const Node& n1) const{return val < n1.val;}
};
vector<Node> adj[MAXN];
ll ANS = 0, ans[MAXN], base[MAXN];void rebuild(int id){ANS -= ans[id]; ans[id] = 0;sort(adj[id].begin(), adj[id].end());for(int k=0;k<adj[id].size();k++){ans[id] += abs((ll)adj[id][k].val + base[id]) * adj[id][k].w;if(k==0) adj[id][k].sw = adj[id][k].w;else adj[id][k].sw = adj[id][k-1].sw + adj[id][k].w;}ANS += ans[id];
}void work(int l, int r, int f){int idl = l/B, idr = r/B;if(idl==idr){for(int k=0;k<adj[idl].size();k++){if(l<=adj[idl][k].id && adj[idl][k].id<=r){if(f==0) adj[idl][k].val -= 1;if(f==1) adj[idl][k].val += 1;}}rebuild(idl);}else{if(idl+1<idr){for(int id=idl+1;id<idr;id++){//int lb = 0, rb = adj[id].size()-1, mid;if(f==0){if(adj[id][rb].val + base[id] <= 0){ans[id] += adj[id][rb].sw;ANS += adj[id][rb].sw;base[id] -= 1;continue;}while(lb < rb){mid = (lb + rb)/2;if(adj[id][mid].val + base[id] > 0) rb = mid;else lb = mid + 1;}base[id] -= 1;int p = rb;if(p==0){ans[id] -= adj[id][adj[id].size()-1].sw;ANS -= adj[id][adj[id].size()-1].sw;}else{ans[id] += adj[id][p-1].sw;ANS += adj[id][p-1].sw;ans[id] -= adj[id][adj[id].size()-1].sw - adj[id][p-1].sw;ANS -= adj[id][adj[id].size()-1].sw - adj[id][p-1].sw;}}else{if(adj[id][rb].val + base[id] < 0){ans[id] -= adj[id][rb].sw;ANS -= adj[id][rb].sw;base[id] += 1;continue;}while(lb < rb){mid = (lb + rb)/2;if(adj[id][mid].val + base[id] >= 0) rb = mid;else lb = mid + 1;}base[id] += 1;int p = rb;if(p==0){ans[id] += adj[id][adj[id].size()-1].sw;ANS += adj[id][adj[id].size()-1].sw;}else{ans[id] -= adj[id][p-1].sw;ANS -= adj[id][p-1].sw;ans[id] += adj[id][adj[id].size()-1].sw - adj[id][p-1].sw;ANS += adj[id][adj[id].size()-1].sw - adj[id][p-1].sw;}}}}for(int k=0;k<adj[idl].size();k++){if(l<=adj[idl][k].id && adj[idl][k].id<=r){if(f==0) adj[idl][k].val -= 1;if(f==1) adj[idl][k].val += 1;}}rebuild(idl);for(int k=0;k<adj[idr].size();k++){if(l<=adj[idr][k].id && adj[idr][k].id<=r){if(f==0) adj[idr][k].val -= 1;if(f==1) adj[idr][k].val += 1;}}rebuild(idr);}
}int pos[MAXN];int main(){scanf("%d", &N);int x;for(int i=1;i<=N;i++){scanf("%d", &x);pos[i] = x;mp[x] += 1;}for(int i=1;i<=N;i++){scanf("%d", &x);mp[x] -= 1;}scanf("%d", &Q);for(int i=1;i<=Q;i++){scanf("%d%d", &q[i][0], &q[i][1]);if(mp.count(q[i][1])==0) mp[q[i][1]] = 0;}int n = 0, x0 = 0;for(it=mp.begin(); it!=mp.end(); ++it){x = it->first;id[x] = ++n;w[n-1] = x - x0;a[n] = a[n-1] + it->second;x0 = x;}N = n; B = sqrt(N); //cerr<<"B = "<<B<<endl;for(int i=1;i<=N;i++){adj[i/B].push_back(Node(i,a[i],w[i]));}for(int id=0;id<=N/B;++id){rebuild(id);}printf("%lld\n", ANS);int l,r;for(int i=1;i<=Q;i++){l = id[pos[q[i][0]]];r = id[q[i][1]];pos[q[i][0]] = q[i][1];//cerr<<"work "<<l<<" "<<r<<endl;if(l < r) work(l, r-1, 0);if(l > r) work(r, l-1, 1);printf("%lld\n", ANS);}return 0;
}