传送门

题目描述

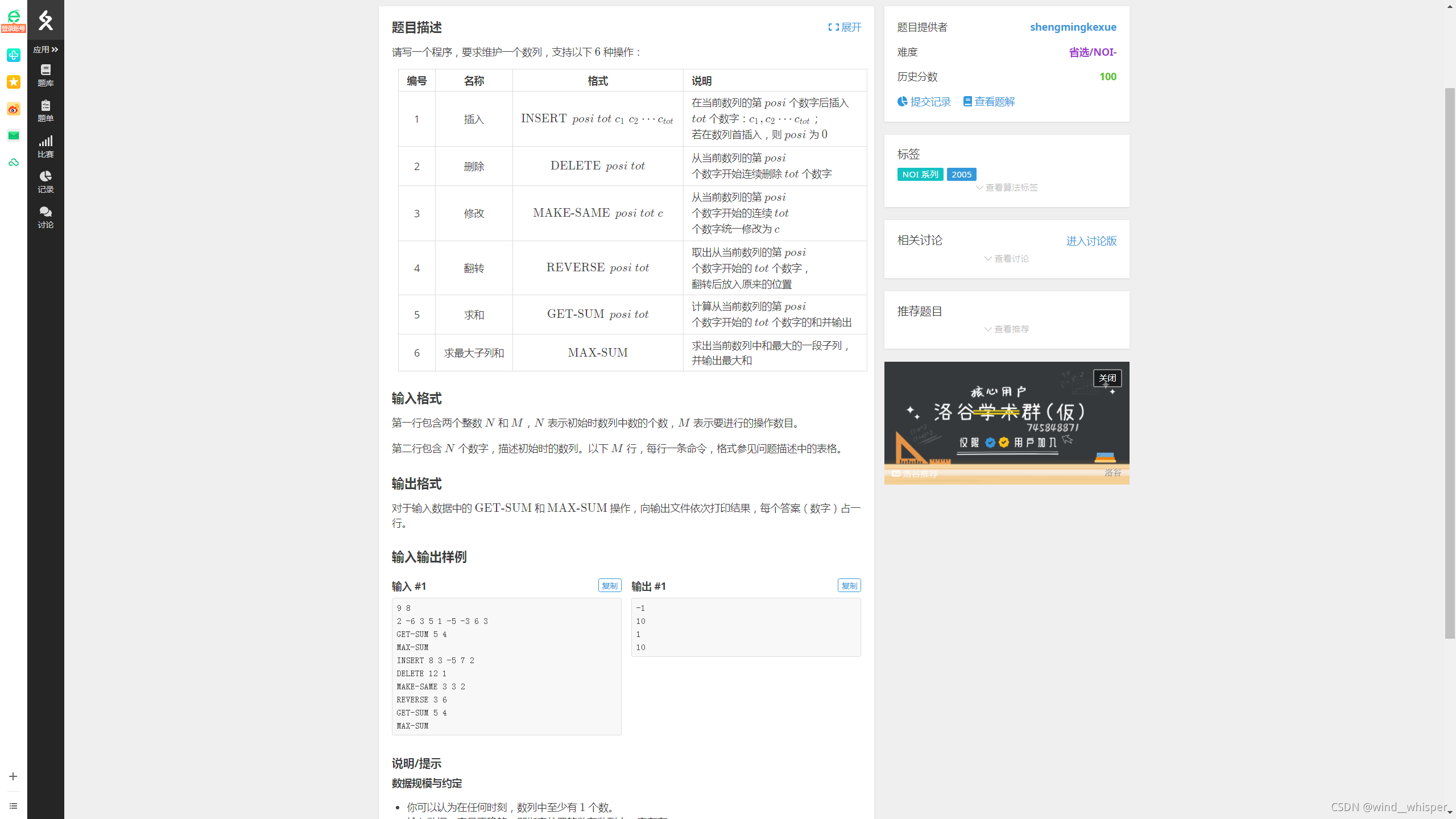
解析

阴间题…
这不是裸的板子吗？
国赛真的有人能把这题写出来吗…
应该算一道练习作用很强的题了
写完这题，各种平衡树维护区间操作的方法可以说是毕业了吧
题解封装一个split函数的实现技巧值得借鉴
总的来说就一句：不要忘记pushdown和pushup！

删除区间

设删除区间为[l,r]
先把l-1结点splay到根
再把r+1转到l-1的下面
这样[l,r]一定就在r+1的右儿子了
直接删掉即可

插入数列

先在外面用类似线段树的方法建一棵完全平衡的平衡树，然后当单点接到需要的位置（寻找位置与删除类似）

修改&翻转

上标记！
把对应区间转出来，打一个标记即可

区间和&最大子段和

区间和比较无脑
最大子段和做一个经典的小白逛公园就行了

说起来很轻松，本题代码实现在传标记时还是很恶心的
总结一些易错的问题：

1. 再说一遍：不要漏掉pushup、pushdown！
2. 注意本题最大子段和可以是负数，所以答案不能和0取max
3. same操作可以用一个tag记录是否需要下传比laz记录下传的值更加舒服
4. 反转的时候最大左子段和最大右子段也要交换
5. 本题卡空间，因此需要动态分配点编号，注意分配之前确定标记都整干净了！
6. 插入时把一个结点接到父亲上之前要把父亲的标记下传！
7. 任何操作几乎都要splay一下沿路更新信息
8. …

都是辛酸泪…
上代码吧
（实现已经比较简洁了算上debug还是干到了小200行…）

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2e6+100;
const int M=2e6+100;
const ll mod=1ll<<31;
ll read(){ll x=0,f=1;char c=getchar();while(!isdigit(c)){if(c=='-')f=-1;c=getchar();};while(isdigit(c)){x=x*10+c-'0';c=getchar();};return x*f;
}
int n,m,k;
int fre[N],top;
int val[N],siz[N],f[N],lp[N],rp[N],mx[N],sum[N],r,rev[N],tag[N],tr[N][2];
#define ls (tr[x][0])
#define rs (tr[x][1])
void pushup(int x){if(!x) return;siz[x]=siz[ls]+siz[rs]+1;sum[x]=sum[ls]+sum[rs]+val[x];if(!ls&&!rs){lp[x]=rp[x]=max(0,val[x]);mx[x]=val[x];}else if(!ls){lp[x]=max(0,val[x]+lp[rs]);rp[x]=max(rp[rs],sum[rs]+val[x]);mx[x]=max(mx[rs],val[x]+lp[rs]);}else if(!rs){rp[x]=max(0,val[x]+rp[ls]);lp[x]=max(lp[ls],sum[ls]+val[x]);mx[x]=max(mx[ls],val[x]+rp[ls]);}else{lp[x]=max(lp[ls],sum[ls]+val[x]+lp[rs]);rp[x]=max(rp[rs],sum[rs]+val[x]+rp[ls]);mx[x]=max(rp[ls]+val[x]+lp[rs],max(mx[ls],mx[rs]));}
}
void rrr(int x){rev[x]^=1;swap(ls,rs);swap(lp[x],rp[x]);
}
void pushdown(int x){if(tag[x]){tag[x]=rev[x]=0;if(ls){val[ls]=val[x];tag[ls]=1;sum[ls]=siz[ls]*val[x];}if(rs){val[rs]=val[x];tag[rs]=1;sum[rs]=siz[rs]*val[x];	}if(val[x]>=0){if(ls) mx[ls]=lp[ls]=rp[ls]=sum[ls];if(rs) mx[rs]=lp[rs]=rp[rs]=sum[rs];}else{if(ls){lp[ls]=rp[ls]=0;mx[ls]=sum[ls];}if(rs){lp[rs]=rp[rs]=0;mx[rs]=sum[rs];}}}if(rev[x]){rev[x]=0;if(ls) rrr(ls);if(rs) rrr(rs);}
}
void dfs1(int x){if(!x) return;pushdown(x);dfs1(ls);printf("%d ",val[x]);dfs1(rs);pushup(x);
}
void dfs2(int x){if(!x) return;pushdown(x);printf("x=%d val=%d ls=%d rs=%d siz=%d\n",x,val[x],ls,rs,siz[x]);dfs2(ls);dfs2(rs);pushup(x);
}
void debug(int f){printf("------r=%d\n",r);if(f==1) dfs1(r);else dfs2(r);printf("\n\n");
}
int New(int v,int fa){int x=fre[top--];val[x]=mx[x]=sum[x]=v;lp[x]=rp[x]=max(0,v);f[x]=fa;siz[x]=1;tag[x]=rev[x]=0;return x;
}
#define which(x) (tr[f[x]][1]==x)
void rotate(int x){int fa=f[x],gfa=f[fa];pushdown(gfa);pushdown(fa);pushdown(x);int k=which(x),son=tr[x][k^1];f[x]=gfa;if(gfa) tr[gfa][which(fa)]=x;f[fa]=x;tr[x][k^1]=fa;f[son]=fa;tr[fa][k]=son;pushup(fa);pushup(x);pushup(gfa);
}
void splay(int x,int goal){if(x==goal) return;for(int fa;(fa=f[x])!=goal;rotate(x)){if(f[fa]!=goal)which(x)==which(fa)?rotate(fa):rotate(x);}if(!goal) r=x;
}
int a[N];
int build(int l,int r,int fa){if(l>r) return 0;int mid=(l+r)>>1;int x=New(a[mid],fa);tr[x][0]=build(l,mid-1,x);tr[x][1]=build(mid+1,r,x);pushup(x);
//	printf("l=%d r=%d x=%d pl=%d siz=%d\n",l,r,x,mid,siz[x]);return x;
}
int find(int x,int k){pushdown(x);if(siz[ls]>=k) return find(ls,k);else if(siz[ls]+1==k) return x;else return find(rs,k-siz[ls]-1);
}
int split(int l,int rr){int a=find(r,l-1);splay(a,0);int b=find(r,rr+1);splay(b,a);return tr[b][0];
}
void add(int x,int k,int s){pushdown(x);tr[x][k]=s;f[s]=x;pushup(x);
}
char s[150];
void ins(){int pos=read(),tot=read();pos++;for(int i=1;i<=tot;i++) a[i]=read();int now=build(1,tot,0);if(pos==1){int x=find(r,1);splay(x,0);int y=find(r,2);splay(y,x);add(y,0,now);splay(y,0);return;}int x=split(pos,pos);add(x,1,now);pushup(x);splay(now,0);
}
void save(int x){if(!x) return;fre[++top]=x;save(ls);save(rs);
}
void del(){int pos=read(),tot=read();pos++;int x=split(pos,pos+tot-1),fa=f[x];save(x);tr[fa][0]=0;pushup(fa);splay(fa,0);
}
void same(){int pos=read(),tot=read(),v=read();pos++;int x=split(pos,pos+tot-1);val[x]=v;tag[x]=1;sum[x]=siz[x]*v;lp[x]=rp[x]=max(0,sum[x]);splay(x,0);
}
void reverse(){int pos=read(),tot=read();pos++;int x=split(pos,pos+tot-1);rrr(x);//printf("x=%d\n",x);debug(2);splay(x,0);
}
void getsum(){int pos=read(),tot=read();pos++;int x=split(pos,pos+tot-1);printf("%d\n",sum[x]);
}
void maxsum(){printf("%d\n",mx[r]);
}
int main(){for(int i=500050;i>=1;i--) fre[++top]=i;n=read();m=read();for(int i=1;i<=n;i++) a[i]=read();r=build(1,n,0);splay(find(r,1),0);add(r,0,New(-20000,r));splay(find(r,n+1),0);add(r,1,New(-20000,r));//debug(1);for(int i=1;i<=m;i++){//	printf("-------------------------------------\n");scanf(" %s",s+1);if(s[1]=='I') ins();else if(s[1]=='D') del();else if(s[3]=='K') same();else if(s[1]=='R') reverse();else if(s[1]=='G') getsum();else maxsum();//debug(1);}return 0;
}
/*
*/