P1494 [国家集训队]小Z的袜子

题意：

有一个长度为 n 的序列c[i] 。现在给出 m个询问，每次给出两个数l,r ，从编号在 l 到 r 之间的数中随机选出两个不同的数，求两个数相等的概率。

题解：

很明显，莫队算法
无修改，可离线查询
我认为本题的难点在于。。。如何求概率（捂脸）
我们设col[i]为当前颜色i出现的次数，ans为当前的可行的配对方案（也就是有多少种烤烟选到一双颜色相同的袜子）
每次移动都会更新答案，如果当前颜色是k，如果是增长区间，ans就要加上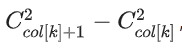，如果是缩短区间长度，就是ans减去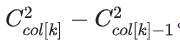
这两个式子应该能明白把
那么这次查询的答案就是，更改后的ans / C²_r-l+1(也就是方案数除以总方案)
哇好麻烦哭了哭了，但是这里是有优化的

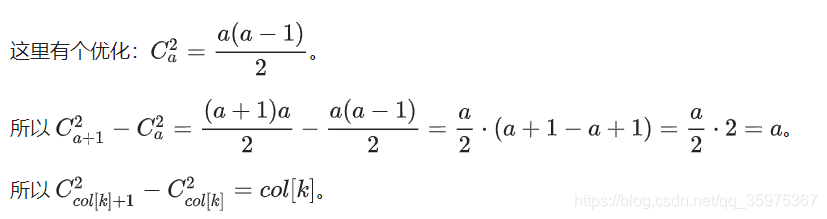
这样一顿操作，增加区间时ans只需要加col[k]
缩短区间时ans只需要减(col[k]–)
总时间复杂度是O(N*√N)

代码：

用的奇偶性排序

#include <algorithm>
#include <cmath>
#include <cstdio>
using namespace std;
const int N = 50005;
int n, m, maxn;
int c[N];
long long sum;
int cnt[N];
long long ans1[N], ans2[N];
struct query {int l, r, id;bool operator<(const query &x) const {if (l / maxn != x.l / maxn) return l < x.l;return (l / maxn) & 1 ? r < x.r : r > x.r;}
} a[N];
void add(int i) {sum += cnt[i];cnt[i]++;
}
void del(int i) {cnt[i]--;sum -= cnt[i];
}
long long gcd(long long a, long long b) { return b ? gcd(b, a % b) : a; }
int main() {scanf("%d%d", &n, &m);maxn = sqrt(n);for (int i = 1; i <= n; i++) scanf("%d", &c[i]);for (int i = 0; i < m; i++) scanf("%d%d", &a[i].l, &a[i].r), a[i].id = i;sort(a, a + m);for (int i = 0, l = 1, r = 0; i < m; i++) {if (a[i].l == a[i].r) {ans1[a[i].id] = 0, ans2[a[i].id] = 1;continue;}while (l > a[i].l) add(c[--l]);while (r < a[i].r) add(c[++r]);while (l < a[i].l) del(c[l++]);while (r > a[i].r) del(c[r--]);ans1[a[i].id] = sum;ans2[a[i].id] = (long long)(r - l + 1) * (r - l) / 2;}for (int i = 0; i < m; i++) {if (ans1[i] != 0) {long long g = gcd(ans1[i], ans2[i]);ans1[i] /= g, ans2[i] /= g;} elseans2[i] = 1;printf("%lld/%lld\n", ans1[i], ans2[i]);}return 0;
}