程序员修仙之路--设计一个实用的线程池

菜菜呀，我最近研究技术呢，发现线上一个任务程序线程数有点多呀

CEO,CTO,CFO于一身的CXO 640?wx_fmt=gif

x总，你学编程呢？

菜菜

作为公司总负责人，我以后还要管理技术部门呢，怎么能不会技术呢

CEO,CTO,CFO于一身的CXO 640?wx_fmt=gif

（技术部完了）。。。。。。。

菜菜

赶紧看看线上那个线程特别多的程序，给你2个小时优化一下

CEO,CTO,CFO于一身的CXO 640?wx_fmt=gif

x总，我想辞职

菜菜

菜菜呀，心不要浮躁，学学小马，心平气和养养生

CEO,CTO,CFO于一身的CXO 640?wx_fmt=gif

............................

菜菜

好了，给你半天时间把线程多的问题优化一下，要不然扣你绩效

CEO,CTO,CFO于一身的CXO 640?wx_fmt=gif

（嘞了个擦）。。。。。。

菜菜

◆◆原因排查◆◆

经过一个多小时的代码排查终于查明了线上程序线程数过多的原因：这是一个接收mq消息的一个服务，程序大体思路是这样的，监听的线程每次收到一条消息，就启动一个线程去执行，每次启动的线程都是新的。说到这里，咱们就谈一谈这个程序有哪些弊端呢：

1. 每次收到一条消息都创建一个新的线程，要知道线程的资源对于系统来说是很昂贵的，消息处理完成还要销毁这个线程。

2. 这个程序用到的线程数量是没有限制的。当线程到达一定数量，程序反而因线程在cpu切换开销的原因处理效率降低。无论的你的服务器cpu是多少核心，这个现象都有发生的可能。

◆◆解决问题◆◆

线程多的问题该怎么解决呢，增加cpu核心数？治标不治本。对于开发者而言，最为常用也最为有效的是线程池化，也就是说线程池。

线程池是一种多线程处理形式，处理过程中将任务添加到队列，然后在创建线程后自动启动这些任务。这避免了在处理短时间任务时创建与销毁线程的代价。线程池不仅能够保证内核的充分利用，还能防止过分调度。可用线程数量应该取决于可用的并发处理器、处理器内核、内存、网络sockets等的数量。例如，线程数一般取cpu数量+2比较合适，线程数过多会导致额外的线程切换开销。

线程池其中一项很重要的技术点就是任务的队列，队列虽然属于一种基础的数据结构，但是发挥了举足轻重的作用。

◆◆队列◆◆

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。

队列是一种采用的FIFO(first in first out)方式的线性表，也就是经常说的先进先出策略。

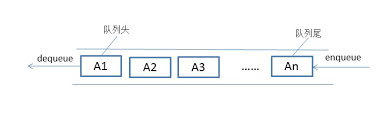
640?wx_fmt=png

实现

数组

队列可以用数组Q[1…m]来存储，数组的上界m即是队列所容许的最大容量。在队列的运算中需设两个指针：head，队头指针，指向实际队头元素+1的位置；tail，队尾指针，指向实际队尾元素位置。一般情况下，两个指针的初值设为0，这时队列为空，没有元素。以下为一个简单的实例（生产环境需要优化）：

public class QueueArray<T>
    {
        //队列元素的数组容器
        T[] container = null;
        int IndexHeader, IndexTail;
        public QueueArray(int size)
        {
            container = new T[size];
            IndexHeader = 0;
            IndexTail = 0;
        }
        public void Enqueue(T item)
        {
            //入队的元素放在头指针的指向位置，然后头指针前移
            container[IndexHeader] = item;
            IndexHeader++;
        }
        public T Dequeue()
        {
            //出队：把尾元素指针指向的元素取出并清空（不清空也可以）对应的位置，尾指针前移
            T item = container[IndexTail];
            container[IndexTail] = default(T);
            IndexTail++;
            return item;
        }

    }

链表

队列采用的FIFO(first in first out)，新元素总是被插入到链表的尾部，而读取的时候总是从链表的头部开始读取。每次读取一个元素，释放一个元素。所谓的动态创建，动态释放。因而也不存在溢出等问题。由于链表由元素连接而成，遍历也方便。以下是一个实例仅供参考：

public class QueueLinkList<T>
    {
        LinkedList<T> contianer = null;
        public QueueLinkList()
        {
            contianer = new LinkedList<T>();
        }
        public void Enqueue(T item)
        {
            //入队的元素其实就是加入到队尾
            contianer.AddLast(item);
        }
        public T Dequeue()
        {
            //出队：取链表第一个元素，然后把这个元素删除
            T item = contianer.First.Value;
            contianer.RemoveFirst();
            return item;
        }

    }

队列的扩展阅读

1. 队列通过数组来实现的话有什么问题吗？是的。首先基于数组不可变本质的因素（具体可参考菜菜之前的文章），当一个队列的元素把数组沾满的时候，数组扩容是有性能问题的，数组的扩容过程不只是开辟新空间分配内存那么简单，还要有数组元素的copy过程，更可怕的是会给GC造成极大的压力。如果数组比较小可能影响比较小，但是当一个数组比较大的时候，比如占用500M内存的一个数组，数据copy其实会造成比较大的性能损失。

2. 队列通过数组来实现，随着头指针和尾指针的位置移动，尾指针最终会指向第一个元素的位置，也就是说没有元素可以出队了，其实要解决这个问题有两种方式，其一：在出队或者入队的过程中不断的移动所有元素的位置，避免上边所说的极端情况发生；其二：可以把数组的首尾元素连接起来，使其成为一个环状，也就是经常说的循环队列。

3. 队列在一些特殊场景下其实还有一些变种，比如说循环队列，阻塞队列，并发队列等，有兴趣的同学可以去研究一下，这里不在展开讨论。这里说到阻塞队列就多说一句，其实用阻塞队列可以实现一个最基本的生产者消费者模式。

4. 当队列用链表方式实现的时候，由于链表的首尾操作时间复杂度都是O（1），而且没有空间大小的限制，所以一般的队列用链表实现更简单

5. 当队列中无元素可出队或者没有空间可入队的时候，是阻塞当前的操作还是返回错误信息，取决于在座各位队列的设计者了。

640?wx_fmt=gif

◆◆简单实用的线程池◆◆

Net Core C# 版本

//线程池
    public class ThreadPool
    {
        bool PoolEnable = false; //线程池是否可用 
        List<Thread> ThreadContainer = null; //线程的容器
        ConcurrentQueue<ActionData> JobContainer = null; //任务的容器
        public ThreadPool(int threadNumber)
        {
            PoolEnable = true;
            ThreadContainer = new List<Thread>(threadNumber);
            JobContainer = new ConcurrentQueue<ActionData>();
            for (int i = 0; i < threadNumber; i++)
            {
                var t = new Thread(RunJob);
                ThreadContainer.Add(t);
                t.Start();
            }           
        }
        //向线程池添加一个任务
        public void AddTask(Action<object> job,object obj, Action<Exception> errorCallBack=null)
        {
            if (JobContainer != null)
            {
                JobContainer.Enqueue(new ActionData { Job = job, Data = obj , ErrorCallBack= errorCallBack });
            }

        }
        //终止线程池
        public void FinalPool()
        {
            PoolEnable = false;
            JobContainer = null;
            if (ThreadContainer != null)
            {
                foreach (var t in ThreadContainer)
                {
                    //强制线程退出并不好，会有异常
                    //t.Abort();
                    t.Join();                    
                }
                ThreadContainer = null;
            }

        }
        private  void RunJob()
        {
            while (true&& JobContainer!=null&& PoolEnable)
            {
                //任务列表取任务
                ActionData job=null;
                JobContainer?.TryDequeue(out job);
                if (job == null)
                {
                    //如果没有任务则休眠
                    Thread.Sleep(10);
                    continue;
                }
                try
                {
                    //执行任务
                    job.Job.Invoke(job.Data);
                }
                catch(Exception error)
                {
                    //异常回调
                    job?.ErrorCallBack(error);
                }
            }
        }
    }

    public class ActionData
    {
        //执行任务的参数
        public object Data { get; set; }
        //执行的任务
        public Action<object> Job { get; set; }
        //发生异常时候的回调方法
        public Action<Exception> ErrorCallBack { get; set; }
    }

使用方法

ThreadPool pool = new ThreadPool(100);
            for (int i = 0; i < 5000; i++)
            {
                pool.AddTask((obj) =>
                {
                    Console.WriteLine($"{obj}__{System.Threading.Thread.CurrentThread.ManagedThreadId}");
                }, i, (e) =>
                {
                    Console.WriteLine(e.Message);
                });
            }
            pool.FinalPool();
            Console.Read();