微软Try .NET项目近期上线，这一项目允许用户通过浏览器运行和编写C#代码，同时还支持完整的代码提示。

用户可以通过访问这一项目官网（点此进入）对Try .NET这一项目进行简单了解。该项目允许开发人员在浏览器中运行和编辑C#代码片段，同时也有相关C#代码教程，还允许访问者对代码进行测试和调试。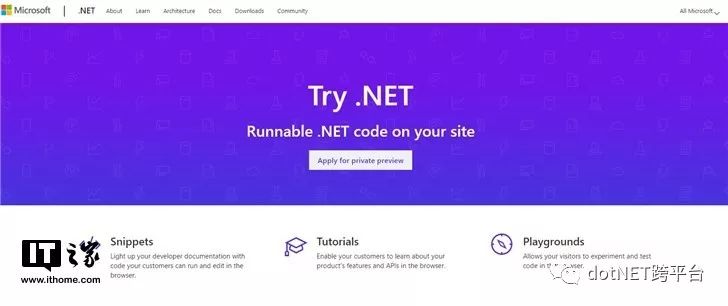

微软的try .NET项目早在2017年就已经开始立项，该项目已经被上传到GitHub（点此进入）上。用户可将使用过程中遇到的问题通过GitHub反馈给开发者。

另外，目前这个项目已经可以初步使用，在浏览器中访问https://try.dot.net/  就能在线进入这一项目。

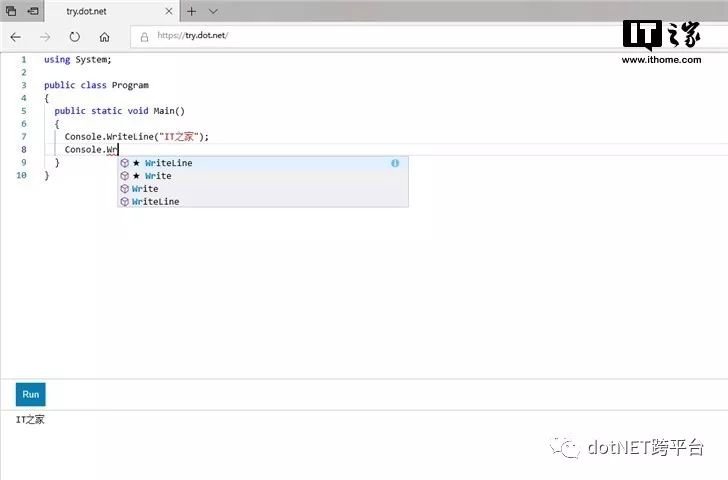
用户可以像在IDE中一样使用各种快捷键完成代码编写，当然，微软这一举措还是希望用户能下载Visual Studio去更深入的体会C#的魅力。

原文地址:https://www.ithome.com/0/405/369.htm

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com