本文出自《从零开始学ASP.NET CORE MVC》
推荐文章：ASP.NET Core 进程外(out-of-process)托管

ASP.NET Core launchsettings.json文件

在本视频中，我们将讨论在ASP.NET Core项目中launchsettings.json文件的重要性。

launchsettings.json文件

• 您将在项目根文件夹的“Properties”文件夹中找到此文件。

• 当我们从Visual Studio或使用.NET Core CLI运行此ASP.NET Core项目时，将使用此文件中的设置。

• 此文件仅用于本地开发环境。我们不需要把它发布到生产环境的Asp.net Core 程序中。

• 如果您希望您的Asp.Net Core 应用程序在发布和部署应用程序时使用某些独立的设置，请将它们存储在appsettings.json文件中。我们通常将应用程序的配置信息存储在此文件中，比如数据库连接字符串。

• 我们还可以使用不同环境的appsettings.json文件。例如，appsettings.Staging.json用于临时环境。在- ASP.NET Core中，除了appsettings.json文件外，我们还可以配置源，如环境变量，用户密钥，命令行参数甚至创建属于我们自己的自定义配置源。

• 有关这些不同配置源的appsettings.json文件的更多用法，我们的下一个视频会讲。

• 
  

ASP.NET Core中的launchSettings文件

打开您的程序，可以看到launchSettings.json文件中的设置 信息如下：

{
"iisSettings": {
"windowsAuthentication": false,
"anonymousAuthentication": true,
"iisExpress": {
"applicationUrl": "http://localhost:3290",
"sslPort": 0
    }
  },
"profiles": {
"IIS Express": {
"commandName": "IISExpress",
"launchBrowser": true,
"environmentVariables": {
"ASPNETCORE_ENVIRONMENT": "Development"
      }
    },
"StudentManagement": {
"commandName": "Project",
"launchBrowser": true,
"applicationUrl": "http://localhost:5000",
"environmentVariables": {
"ASPNETCORE_ENVIRONMENT": "Development"
      }
    }
  }
}

请注意，我们有两个配置信息:

• IIS Express和StudentManagement

当我们通过按CTRL + F5或只是F5从Visual Studio运行项目时。
默认情况下，使用调用配置文件名称"commandName": "IISExpress",。
另外一种情况，如果我们使用.NET Core CLI（dotnet run）运行项目，则使用带有"commandName": "Project",的配置文件 。

我们可以通过单击Visual Studio中的下拉列表来更改要使用的配置文件中 .commandName属性，修改默认设置。

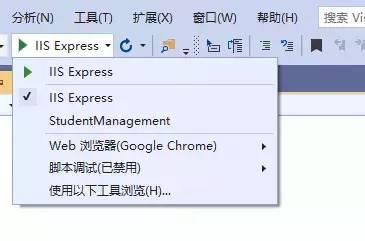
默认值可以是：

• 项目

• IISExpress

• IIS

此值与项目文件中的AspNetCoreHostingModel元素的值会有对应关系，会一起指定要启动的内部和外部Web服务器（反向代理服务器）。

commandName	AspNetCoreHostingModel的值	Internal Web Server(内部服务器)	External Web Server(外部服务器)
项目	忽略托管设置的值	只使用一个Web服务器 - Kestrel	只使用一个Web服务器 - Kestrel
IISExpress	进程内托管(InProcess)	只使用一个Web服务器 - IIS Express	只使用一个Web服务器 - IIS Express
IISExpress	进程外托管(OutOfProcess)	Kestrel	IIS Express
IIS	进程内托管(InProcess)	只使用一个Web服务器 - IIS	只使用一个Web服务器 - IIS
IIS	进程外托管(OutOfProcess)	Kestrel	IIS

您还可以通过直接编辑launchSettings.json文件中的设置，也可以使用Visual Studio提供的图形用户界面（GUI）更改设置。

通过GUI来设置

NEW

﹀

﹀

﹀

• 在Visual Studio的解决方案资源管理器中右键单击项目名称，然后从上下文菜单中选择“属性”。
  单击项目“属性”窗口中的“调试”选项卡,如下图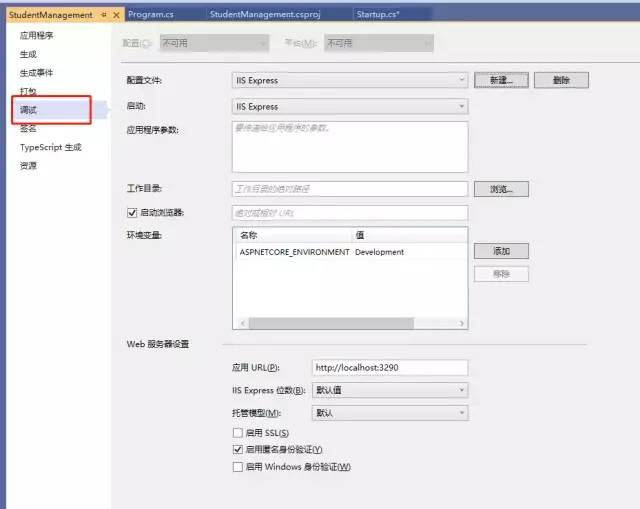
  

  

  image.png

使用GUI我们可以更改launchSettings.json文件中的设置。

注意，环境变量“ASPNETCORE_ENVIRONMENT”设置的默认设置为“Development”。

我们可以将此值更改为Staging或Production，具体取决于我们是在Staging还是Production环境中运行此项目。

我们还可以添加新的环境变量。这些环境变量在我们的Asp.Net Core应用程序中都可用，我们可以包含根据这些环境变量的值有条件地执行的代码。

例如，请参考Startup.cs文件中的Configure（）方法中的以下代码

public void Configure(IApplicationBuilder app, IHostingEnvironment env)
{
if (env.IsDevelopment())
            {
                app.UseDeveloperExceptionPage();
            }

// 其他的代码

        }

仅当环境为“ Development”时，才会显示“ 开发异常页面”。

我们将在即将发布的视频中详细讨论环境变量和开发人员异常页面。

硬广专区

如果您觉得我的文章质量还不错，欢迎打赏，也可以订阅我的视频哦

未得到授权不得擅自转载本文内容,52abp.com保留版权

文字版目录： https://www.52abp.com/Wiki/mvc/latest/1.Intro 

代码托管地址：https://gitee.com/aiabpedu
知乎专栏：https://zhuanlan.zhihu.com/52abp

交流QQ群：952387474《微软MVP带你学ASP.NET CORE》
【收费】腾讯课堂: https://ke.qq.com/course/392589?tuin=2522cdf3 
【免费】youtube视频专区：http://t.cn/Ei0F2EB 
【免费】B站: https://space.bilibili.com/2954671 
免费的更新慢，收费的更新快，仅此而已。就这样。 

「好看」的人都【在看】↓↓↓