problem

luogu-P3756

solution

据说要做网络流 $\text{24}$ 题中的《方格取数问题》和《骑士共存问题》。

？？？那个不是直接最小割吗？哦原来是从黑白染色来理解的。我还是太水了。

这种题之所以能用网络流做，是因为其题目描述中的一些奇奇怪怪的限制是存在一种共同顺序而言的。

且一般都是网格图中搞些幺蛾子。

这个顺序可以将网格图中的每个顺序唯一的确定一种颜色。

然后颜色之间如果形成一个特定的顺序就会触发限制。

网络流的最小割就有用武之地了。

此题的四种限制，不管怎么旋转，翻转，都能有一定的访问顺序。

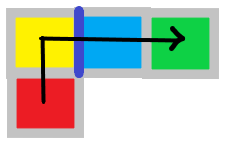
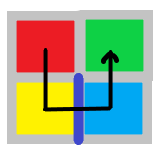
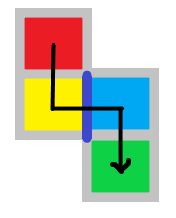
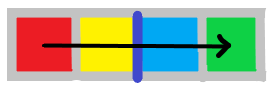
于是乎我们就有了一个构造方式，将所有的网格图都染上颜色，使得当 红→黄→蓝→绿 成功联通时就一定触发限制。

然后我们就可以建图了！源→红→黄→蓝→绿→汇。

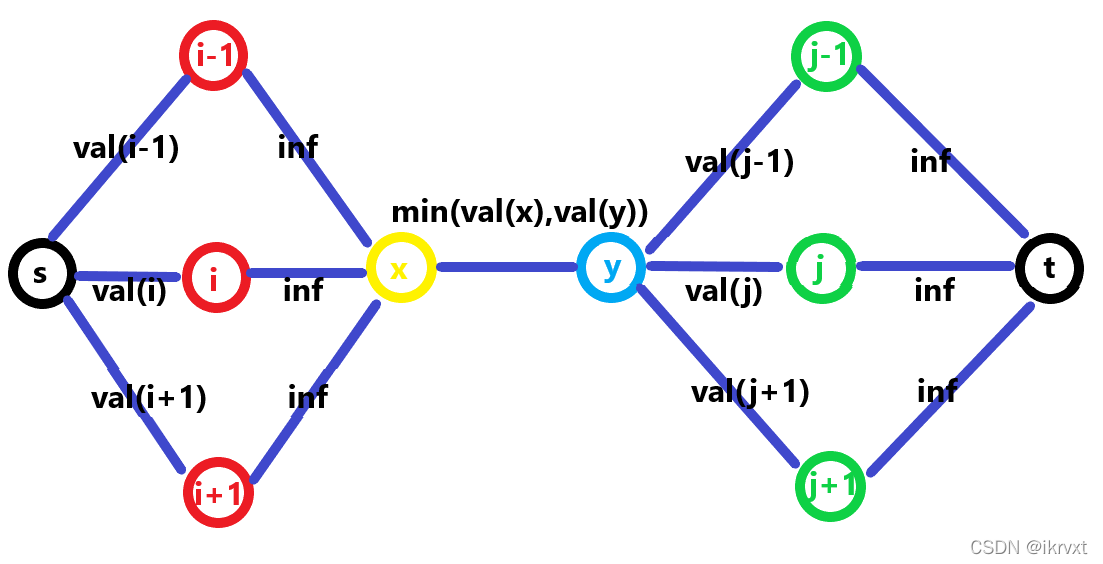
也就是这种元连通块：

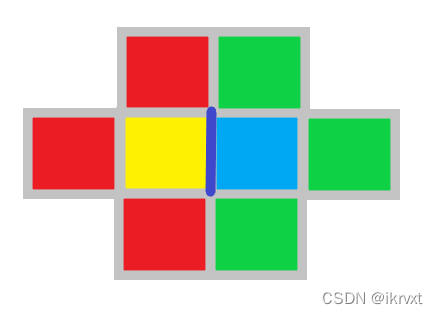
看吧网络流跑 $n=1e5$ 的数据。

所以说网络流复杂度是 O(能过)。

发现奇偶行的颜色循环不太一样，稍微找下规律就可以了。

这题还有个坑的地方！就是他是先列后行。所以注意下细节。

code

#include <bits/stdc++.h>
using namespace std;
#define maxn 100005
#define inf 0x3f3f3f3f
struct node { int to, nxt, flow; }E[maxn << 3];
int head[maxn], cur[maxn], dep[maxn];
queue < int > q;
int s, t, n, cnt = -1;void addedge( int u, int v, int w ) {E[++ cnt] = { v, head[u], w }, head[u] = cnt;E[++ cnt] = { u, head[v], 0 }, head[v] = cnt;
}
bool bfs() {memset( dep, 0, sizeof( dep ) );memcpy( cur, head, sizeof( head ) );dep[s] = 1, q.push( s );while( ! q.empty() ) {int u = q.front(); q.pop();for( int i = head[u];~ i;i = E[i].nxt ) {int v = E[i].to;if( ! dep[v] and E[i].flow ) {dep[v] = dep[u] + 1;q.push( v );}}}return dep[t];
}
int dfs( int u, int cap ) {if( u == t or ! cap ) return cap;int flow = 0;for( int i = cur[u];~ i;i = E[i].nxt ) {cur[u] = i; int v = E[i].to;if( dep[v] == dep[u] + 1 ) {int w = dfs( v, min( cap, E[i].flow ) );if( ! w ) continue;E[i ^ 1].flow += w;E[i].flow -= w;flow += w;cap -= w;if( ! cap ) break;}}return flow;
}
int dinic() {int ans = 0;while( bfs() ) ans += dfs( s, inf );return ans;
}#define red    4
#define yellow 1
#define blue   2
#define green  3
int r, c;
int val[maxn];
map < int, int > mp[maxn];
int color( int x, int y ) {if( x & 1 ) return (y - 1) % 4 + 1;else return 4 - (y - 1) % 4;
}
bool inside( int x, int y ) {if( x < 1 or x > r or y < 1 or y > c ) return 0;else return 1;
}
int dx[4] = { 1, -1, 0, 0 }, dy[4] = { 0, 0, 1, -1 };int main() {memset( head, -1, sizeof( head ) );scanf( "%d %d %d", &c, &r, &n );for( int i = 1, x, y, w;i <= n;i ++ ) {scanf( "%d %d %d", &y, &x, &w );mp[y][x] = i, val[i] = w;}s = 0, t = n + 1;for( int i = 1;i <= c;i ++ )for( auto j = mp[i].begin();j != mp[i].end();j ++ ) {int y = i, x = j->first, id = j->second;if( color( x, y ) == red ) addedge( s, id, val[id] );else if( color( x, y ) == green ) addedge( id, t, val[id] );else {for( int k = 0;k < 4;k ++ ) {int tx = x + dx[k], ty = y + dy[k];if( inside( tx, ty ) and mp[ty].count( tx ) ) {int tid = mp[ty][tx];if( color( x, y ) == yellow ) {if( color( tx, ty ) == blue )addedge( id, tid, min( val[id], val[tid] ) );if( color( tx, ty ) == red )addedge( tid, id, inf );}elseif( color( tx, ty ) == green ) addedge( id, tid, inf );}}}}printf( "%d\n", dinic() );return 0;
}