今天很多人都收到了阿里云函数计算支持.NET Core的短信了。

通过访问 https://help.aliyun.com/document_detail/112379.html 你可以看到最新的说明。现在和过去的两年不同，因为最恶劣的时期已经过去，经历过了最黑暗的时刻，我们正在走向光明的前程。.NET Core 在今年即将引来3.0版本，

在经过了1.x的沉淀后，2.x版本趋向于风格上的稳定，有兴趣知道各个版本的一些特性和变化，可以参考ASPNET.Core各个版本差异以及新特性 ，有兴趣的还可以关注3.x的预览版。

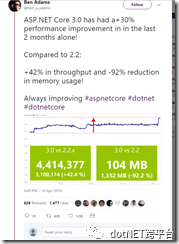
这个性能优化非常感人，具体大家可以看看这个PR https://github.com/aspnet/AspNetCore/pull/8374。

从上面这两天这两个小小事件你应该感受到了.NET Core的新时代已经开启。随着互联网和电商公司从去年开始一家家的倒掉，你们会发现.NET正在重新成为市场焦点。BAT 都开始转向企业市场，在传统的企业市场有大量的.NET 应用，以至于这些搞互联网的同学接触到这些系统时都在感慨你们还在用”这么老的没人用的.NET”, 这两年发生了很多 .NET 被强制转Java的事件，现在还在上演。我希望随着.NET Core的成熟，这样的事件需要反转，从Java转.NET Core.

原文地址：https://www.cnblogs.com/shanyou/p/10699029.html

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com