从上篇内容不如题的文章《.net core 并发下的线程安全问题》扩展认识.net core注入中的三种模式：Singleton、Scoped 和 Transient

我们都知道在 Startup 的 ConfigureServices 可以注入我们想要的服务，那么在注入的时候有三种模式可以选择，那么我们在什么时候选择什么样的模式呢？

在讲注入模式之前，我觉得很有必要了解服务生存期的概念！

服务生存期：ASP.NET Core 提供了一个内置的服务容器 IServiceProvider 负责管理服务的生命周期，从被依赖注入容器创建开始（就是将服务注入到你要使用的类的构造函数中），然后框架负责创建依赖关系的实例，并在不再需要时对其进行处理（就是说等我们调用完服务时，容器会自己去对注入的服务进行释放）。

IServiceProvider 怎么负责的呢？

// System.IServiceProvider
using System;

public interface IServiceProvider
{
object GetService(Type serviceType);
}

可以看出是通过 GetService 此接口的方法获取提供服务的对象。那再走深一点找找，我们看看 程序集 Microsoft.Extensions.DependencyInjection 是怎么提供这个容器的

//Microsoft.Extensions.DependencyInjection.IServiceProviderFactory<TContainerBuilder>
using Microsoft.Extensions.DependencyInjection;
using System;

public interface IServiceProviderFactory<TContainerBuilder>
{
    TContainerBuilder CreateBuilder(IServiceCollection services);

    IServiceProvider CreateServiceProvider(TContainerBuilder containerBuilder);
}

看到上面的 IServiceProviderFactory 接口是不是很熟悉了，这个容器里会有一个 IServiceCollection（服务集合），那服务怎么加进入（实现）的呢

//Microsoft.Extensions.DependencyInjection.ServiceCollectionServiceExtensions
using System;

private static IServiceCollection Add(IServiceCollection collection, Type serviceType, Type implementationType, ServiceLifetime lifetime)
{
    ServiceDescriptor item = new ServiceDescriptor(serviceType, implementationType, lifetime);
    collection.Add(item);
return collection;
}

 到这里，已经很清楚了，也已经接近我们今天的主题了，直接来吧

// Microsoft.Extensions.DependencyInjection.ServiceLifetime
public enum ServiceLifetime
{
    Singleton,
    Scoped,
    Transient
}

上面的枚举里面就是提供了 Singleton、Scoped 和 Transient 三种模式。去 微软的文档 里面看看，先了解一下这三种模式，在 ServiceCollectionServiceExtensions 就只有3个方法（有重载哟）

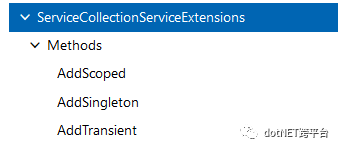
从源码里面绝对可以想到，这3个方法是继承 IServiceCollection。好了，说说这三种模式先，毕竟实现我们不是很关心（关心就看文档看源码）

（1）Singleton 单一实例模式：单一实例对象对每个对象和每个请求都是相同的，可以说是不同客户端不同请求都是相同的。

（2）Transient 暂时性模式：暂时性对象始终不同，无论是不是同一个请求（同一个请求里的不同服务）同一个客户端，每次都是创建新的实例。

（3）Scoped 作用域模式：作用域对象在一个客户端请求中是相同的，但在多个客户端请求中是不同的。（这句是文档的原话，我觉得描述的很清晰）

什么时候用哪种模式？这个不大好说（希望这个可以成为讨论点）

比如一下吧：

1、日志记录器可以实现为单例，因为在整个生命周期内都可以只使用一个实例；

2、数据库访问上下文（DbContext）选择 Scoped 的应该是最佳候选，因为 services.AddDbContext 默认就是 Scoped（哈哈哈）；

3、如果需要利用深度依赖关系图（a deep dependency graph）创建惟一对象，则可以考虑将该对象注册为 transient 。

还有看看别人怎么说（对Scoped的描述，在理解上可能不大一样，见仁见智了老铁）

 还有一个 stackoverflow 的

按别人的经验，可以作为参考参考：

  

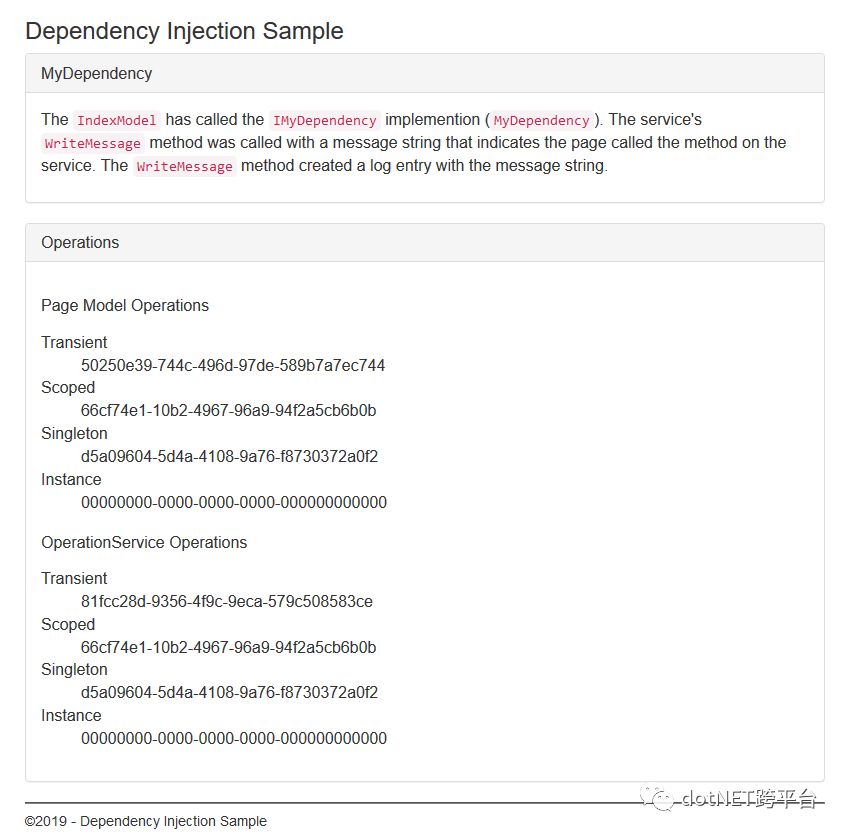
怎么验证？请用 官方例子 运行一下看结果：

浏览器第一个tab页面（第一个请求，可以认为是一个客户端）：

浏览器第二个tab页面（第二个请求，可以认为是另一个客户端）：

 

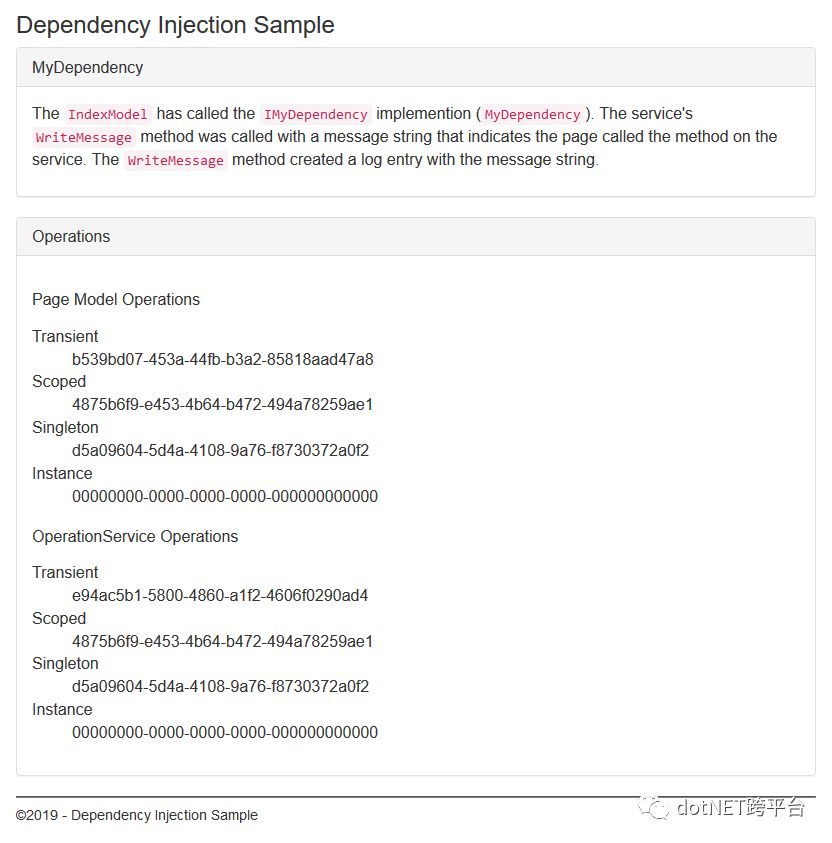
 看上面的结果就不多说了。

这篇扩展认识写得还蛮有意思的，尤其是在找这三种模式的使用场景，虽然自己有点见解，但绝对不完整。如更好的见解，很希望能一起分享一下。

下一篇的扩展好像要回到源头，撸撸 .net core 的注入了，哈哈哈……

原文地址：https://www.cnblogs.com/Vam8023/p/10684651.html

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com