传送门

题意：有一序列$S$由下列方式生成：

1. 找到字典序最小的正整数$(a,b,c)$，满足$a,b,c$不在$S$中且$a\oplus b\oplus c=0$,其中$\oplus$为异或
2. 将$a,b,c$加入$S$
3. 重复第一步

$T$组数据，求$S$的第$n$项。

$T\le 10^5,n\le 10^{16}$

通过观察样例和理性猜想，可以假设前$4^k-1$项恰好填完了$1\sim 4^k-1$，显然这是整数个三元组。采用归纳法构造$4^k\sim 4^{k+1}-1$

将每个序列中的数按二进制位两个为一组拆分（以下称拆成的两个二进制位为"位"），当前的数(已构造的和此步将构造的)有$2(k+1)$位

之前填的$4^k-1$项可以看成最高位为$\text{00}$，我们要构造的是最高位为$\text{01,10,11}$，后面$k$位分别遍历$0\sim 4^k-1$

对于每一个$(a,b,c)$显然有$a<b<c$

构造$a$最高位为$\text{01}$,容易得到$b,c$最高位为$\text{10,11}$。这是最理想的结果，下面将证明这种构造是可行的。

现在已经满足了$a<b<c$，那么$a,b,c$的后$k$位是互不影响的。下面讨论的都是这后$k$位。

现在考虑如何最小化字典序

对于一个已经确定的$a$，我们都需要找到最小的$b$(废话)

对于$a$上的每一位，都找到一个最小的对应的$b$的位即可（似乎还是废话，但似乎就是想不到）

设新构造的三元组为$(a_i,b_i,c_i)(0\le i\le 2^k-1)$显然所有的$a_i=i$

根据以上信息可以构造出$(a,b,c)$每一位字典序最小的对照表

盗用官方题解的图：

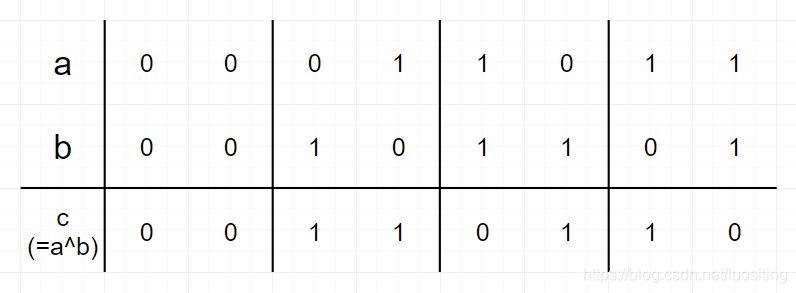
随便推一下就可以了

复杂度$O(T\log n)$