先来张《计算机视觉:算法与应用》中的3D重建示例图镇楼!
好吧,现在言归正传,来看看几何学上世界是怎样投影进摄相机里的吧!接下来让我们来看一下本系列博客的第一“搏”:
图像坐标:我想和世界坐标谈谈(A)
首先,我先解释一下这个题目吧。题目的字面意义是说:图像坐标系想和世界坐标系谈谈。这里面包含着两个问题:
A、谈话对象:视觉系统的三大坐标系:世界坐标系,摄像机坐标系和图像坐标系。这是玉米在本文《我想和世界坐标谈谈 (A)》中想要和大家分享的内容。其中主要包含:三大坐标系的位置、作用和应用场景。
B、谈话方式:两个不同的坐标系之间该如何沟通呢?玉米将在《我想和世界坐标谈谈(B)》中和大家分享一下刚体变换和透视 投影变换。连起两个坐标系之间这不在一个参考系的“世界上最远的距离”。
好吧,下面让我们来揭开三大坐标系的庐山真面目。
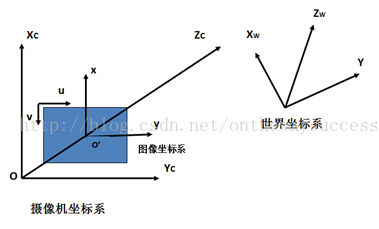
上图是三个坐标的示意简图,通过它大家可以对三个坐标有一个直观的认识。下面来看看三个坐标系的骨子里藏了什么。
世界坐标系(XW,YW,ZW):其是目标物体位置的参考系。除了无穷远,世界坐标可以根据运算方便与否自由放置。在双目视觉中世界坐标系主要有三个用途:1、标定时确定标定物的位置2、作为双目视觉的系统参考系,给出两个摄像机相对世界坐标系的关系,从而求出相机之间的相对关系3、作为重建得到三维坐标的容器,盛放重建后的物体的三维坐标。世界坐标系是将看见中物体纳入运算的第一站。
摄像机坐标系(XC,YC,ZC):其是摄像机站在自己角度上衡量的物体的坐标系。摄像机坐标系的原点在摄像机的光心上,z轴与摄像机光轴平行。它是与拍摄物体发生联系的桥头堡,世界坐标系下的物体需先经历刚体变化转到摄像机坐标系,然后在和图像坐标系发生关系。它是图像坐标与世界坐标之间发生关系的纽带,沟通了世界上最远的距离。哈哈
图像坐标系(x,y)/(u,v) :其是以摄像机拍摄的二维照片为基准建立的坐标系。用于指定物体在照片中的位置。玉米更倾向将(x,y)称为连续图像坐标或空间图像坐标,将(u,v)称为离散图像坐标系或者是像素图像坐标系(虽然这样的称呼未经考证,但更能传达二者的物理意义)。
(x,y)坐标系的原点位于摄像机光轴与成像平面的焦点O’(u0,v0)上,单位为长度单位(米)。(u,v)坐标系的原点在图片的左上角(其实是存储器的首地址)如上图所示,单位为数量单位(个)。(x,y)主要用于表征物体从摄像机坐标系向图像坐标系的透视投影关系。而(u,v)则是实实在在的,我们能从摄像机中得到的真实信息。
(x,y)与(u,v)存在如下转换关系:
dx代表x轴方向一个像素的宽度,dy代表y轴方向上一个像素的宽度。dx、dy为摄像机的内参数。(u0,v0)称为图像平面的主点,也是摄像机的内参数。其实相当于对x轴和y轴的离散化。其可以运用齐次坐标,将上式写成矩阵形式,如下:
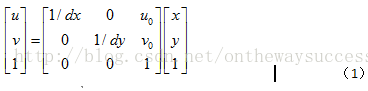
(1)式运用了齐次坐标,初学者可能会感到有些迷惑。大家会问:怎样将普通坐标转换为齐次坐标呢?齐次坐标能带来什么好处呢?
玉米在这里对齐次坐标做一个通俗的解释。此处只讲怎么将普通坐标改写为齐次坐标及为什么引入齐次坐标。这里只做一个通俗但不太严谨的表述。力求简单明了。针对齐次坐标的严谨的纯数学推导,可参见“周兴和版的《高等几何》---1.3拓广平面上的齐次坐标”。玉米曾详细读过《高等几何》这本书,但觉得离计算机视觉有点远,是讲纯数学的投影关系的,较为生涩难懂。
齐次坐标可以理解为在原有坐标后面加一个“小尾巴”。将普通坐标转换为齐次坐标,通常就是在增加一个维度,这个维度上的数值为1。如图像坐标系(u,v)转换为(u,v,1)一样。对于无穷远点,小尾巴为0。注意,给零向量增加小尾巴,数学上无意义。
那么,为什么计算机视觉在坐标运算时要加上这个“小尾巴”呢?
玉米看来有两点原因:
1、 将投影平面扩展到无穷远点。如对消隐点(vanishing point)的描述。
2、 使得计算更加规整
如式(1)如果用普通坐标来表达的话,会是下面的样子:
这样的运算形式会给后与运算带来一定的麻烦,所以齐次坐标是一个更好的选择。
齐次坐标还有一个重要的性质,伸缩不变性。即:设齐次坐标M,则αM=M。

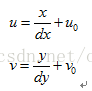
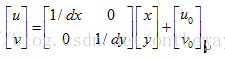



)









)

)


合并分支的方法与策略)
