三、致敬“张正友标定”
此处“张正友标定”又称“张氏标定”,是指张正友教授于1998年提出的单平面棋盘格的摄像机标定方法。张氏标定法已经作为工具箱或封装好的函数被广泛应用。张氏标定的原文为“A Flexible New Technique forCamera Calibration”。此文中所提到的方法,为相机标定提供了很大便利,并且具有很高的精度。从此标定可以不需要特殊的标定物,只需要一张打印出来的棋盘格。So great! 这样的方法让人肃然起敬。所以玉米的这篇博客的题目是:致敬“张氏标定”。
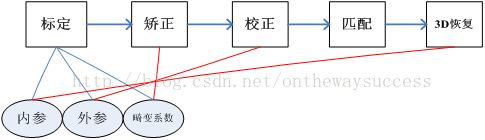
当然,此博的内容也是围绕着“张氏标定”进行的,在这里,玉米主要介绍一下,“张氏标定”的数学思路。因为标定在整个基于标定摄像机的三维重建的几何过程占有最重要最核心的地位。如下图:
从图中明显可以看出,标定得到的内参、外参和畸变系数,是双目视觉进行图片矫正,摄像机校正和3D恢复的基础。没有好的标定,双目视觉系统就无法完成3D重建。
既然标定对双目视觉如此重要,我们有必要对数学的深层含义多加理解。以张氏标定为例,让我们挖开工具箱,看看其数学本质吧。因为张教授的论文中对标定方法的讲述是循序渐进的,所以玉米在这里将按照张教授论文中的顺序,为大家讲述一下,张氏标定的脉络。
1、标定平面到图像平面的单应性
因为张氏标定是一种基于平面棋盘格的标定,所以想要搞懂张氏标定,首先应该从两个平面的单应性(homography)映射开始着手。
单应性(homography):在计算机视觉中被定义为一个平面到另一个平面的投影映射。首先看一下,图像平面与标定物棋盘格平面的单应性。
由上两篇博文中讲到的摄像机模型,肯容易得到:
其中m的齐次坐标表示图像平面的像素坐标(u,v,1),M的齐次坐标表示世界坐标系的坐标点(X,Y,Z,1)。A[R t]即是上面一篇博客推出的P。R表示旋转矩阵、t表示平移矩阵、S表示尺度因子。A表示摄像机的内参数,具体表达式如下:
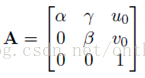
α=f/dx,β=f/dy,因为像素不是规规矩矩的正方形,γ代表像素点在x,y方向上尺度的偏差。
这里还有一个“梗儿”,就是S。它只是为了方便运算,对于齐次坐标,尺度因子不会改变坐标值的。
因为标定物是平面,所以我们可以把世界坐标系构造在Z=0的平面上。然后进行单应性计算。令Z=0可以将上式转换为如下形式:
既然,此变化属于单应性变化。那么我们可以给A[r1 r2 t]一个名字:单应性矩阵。并记H= A[r1 r2 t]。
那么现在就有:
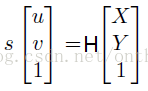
大家可以分析一下,H是一个三3*3的矩阵,并且有一个元素是作为齐次坐标。因此,H有8个未知量待解。
(x,y)作为标定物的坐标,可以由设计者人为控制,是已知量。(u,v)是像素坐标,我们可以直接通过摄像机获得。对于一组对应的(x,y)-à(u,v)我们可以获得两组方程。
现在有8个未知量需要求解,所以我们至少需要八个方程。所以需要四个对应点。四点即可算出,图像平面到世界平面的单应性矩阵H。
这也是张氏标定采用四个角点的棋盘格作为标定物的一个原因。
在这里,我们可以将单应性矩阵写成三个列向量的形式,即:
2、利用约束条件求解内参矩阵A
从上面可知,应用4个点我们可以获得单应性矩阵H。但是,H是内参阵和外参阵的合体。我们想要最终分别获得内参和外参。所以需要想个办法,先把内参求出来。然后外参也就随之解出了。我们可以仔细的“观摩”一下下面的式子。
从中可以得出下面两个约束条件,这两个约束条件都是围绕着旋转向量来的。
1、r1,r2正交 得:r1r2=0。这个很容易理解,因为r1,r2分别是绕x,y轴旋转的。应用高中立体几何中的两垂直平面上(两个旋转向量分别位于y-z和x-z平面)直线的垂直关系即可轻松推出。
2、旋转向量的模为1,即|r1|=|r2|=1。这个也很容易理解,因为旋转不改变尺度嘛。如果不信可以回到上一篇博客,找到个方向的旋转矩阵化行列式算一下。
通过上面的式子可以将r1,r2代换为h1,h2与A的组合进行表达。即 r1=h1A-1,r2=h2A-1.根据两约束条件,可以得到下面两个式子:
大家从上面两个式子是不是看出一点端倪了。式子中,h1,h2是通过单应性求解出来的那么未知量就仅仅剩下,内参矩阵A了。内参阵A包含5个参数:α,β,u0,v0,γ。那么如果我们想完全解出这五个未知量,则需要3个单应性矩阵。3个单应性矩阵在2个约束下可以产生6个方程。这样可以解出全部的五个内参了。大家想一下,我们怎样才能获得三个不同的单应性矩阵呢?答案就是,用三幅标定物平面的照片。我们可以通过改变摄像机与标定板间的相对位置来获得三张不同的照片。(当然也可以用两张照片,但这样的话就要舍弃掉一个内参了γ=0)
到这里,大家应该就明白我们在张氏标定法时为什么要不断变换标定板的方位了吧。当然这只是一个原因。第二个原因,玉米会在讲极大似然时讲到。
下面在对我们得到的方程做一些数学上的变化,这些变化都是简单的运算变化了,相信大家动动笔,一算就可以算出。这些变化都是为了运算方便的,所以也没什么物理意义。
首先令:
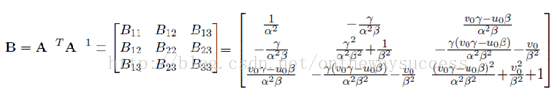
很容易发现B是一个对称阵,所以B的有效元素只剩下六个(因为有三对对称的元素是相等的,所以只要解得下面的6个元素就可以得到完整的B了),让这六个元素构成向量b。
接下来在做一步纯数学化简:
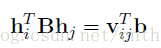
可以计算得:
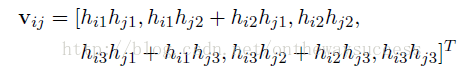
利用约束条件可以得到下面,方程组:
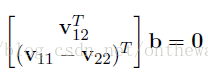
这个方程组的本质和前面那两个用h和A组成的约束条件方程组是一样的。在此重复一遍解释:如果我们想完全解出这五个未知量,则需要3个单应性矩阵。3个单应性矩阵在2个约束下可以产生6个方程。这样可以解出全部的五个内参了。大家想一下,我们怎样才能获得三个不同的单应性矩阵呢?答案就是,用三幅标定物平面的照片。我们可以通过改变摄像机与标定板间的相对位置来获得三张不同的照片。(当然也可以用两张照片,但这样的话就要舍弃掉一个内参了γ=0)
通过至少含一个棋盘格的三幅图像,应用上述公式我们就可以估算出B了。得到B后,我们通过cholesky分解 ,就可以轻松地得到摄像机的内参阵A。3、基于内参阵估算外参阵
通过上面的运算,我们已经获得了摄像机的内参阵。那么对于外参阵,我们很容易通过下面的公式解得:
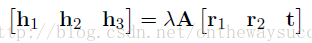
对上面公式进行化简,可以得到:
至此,玉米已经将张氏标定的主体数学框架已经讲完了。介于篇幅关系(怕太长大机会读的昏昏欲睡,哈哈)。但其实我们做了这么多推导,仅仅是为后面的极大似然参数估计提供初值。但当然这个初值也是不可或缺的,因为没有这个初值,就无法估计出更为准确的参数。玉米将张氏标定中用于提高标定精度的极大似然算法,放到下一篇博客中进行讲解。
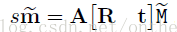
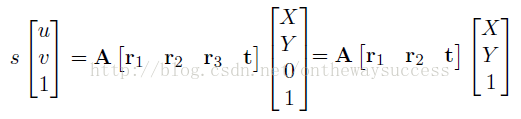
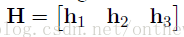
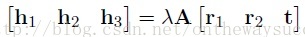

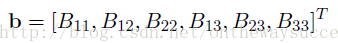
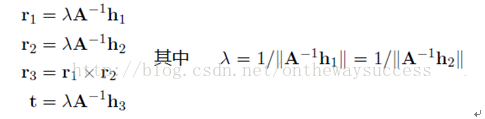





)

)


合并分支的方法与策略)








