二、图像坐标:我想和世界坐标谈谈(B)
玉米将在这篇博文中,对图像坐标与世界坐标的这场对话中涉及的第二个问题:谈话方式,进行总结。世界坐标是怎样变换进摄像机,投影成图像坐标的呢?
玉米做了一个简单的图示,在这里做一个提纲。图中显示,世界坐标系通过刚体变换到达摄像机坐标系,然后摄像机坐标系通过透视投影变换到达图像坐标系。可以看出,世界坐标与图像坐标的关系建立在刚体变换和透视投影变换的基础上。为了奖励刚体变和透视投影变换沟通了“世界上最远的距离”,玉米在图上奖励了他们两朵小红花。哈哈
首先,让我们来看一下刚体变换是如何将世界坐标系与图像坐标系联系起来的吧。这里,先对刚体变换做一个介绍:
刚体变换(regidbody motion):三维空间中, 当物体不发生形变时,对一个几何物体作旋转, 平移的运动,称之为刚体变换。
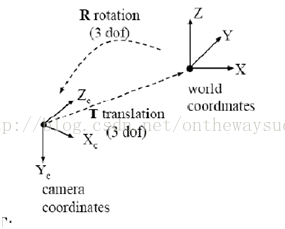
因为世界坐标系和摄像机坐标都是右手坐标系,所以其不会发生形变。我们想把世界坐标系下的坐标转换到摄像机坐标下的坐标,如下图所示,可以通过刚体变换的方式。空间中一个坐标系,总可以通过刚体变换转换到另外一个个坐标系的。转一转,走一走,就到另外一个坐标系下了。以前可能是面朝大海,经过平移旋转,最终可能只能面朝冰山了,哈哈
下面让我来看一下,二者之间刚体变化的数学表达。
其中,XC代表摄像机坐标系,X代表世界坐标系。R代表旋转,T代表平移。R、T与摄像机无关,所以称这两个参数为摄像机的外参数(extrinsic parameter)可以理解为两个坐标原点之间的距离,因其受x,y,z三个方向上的分量共同控制,所以其具有三个自由度。
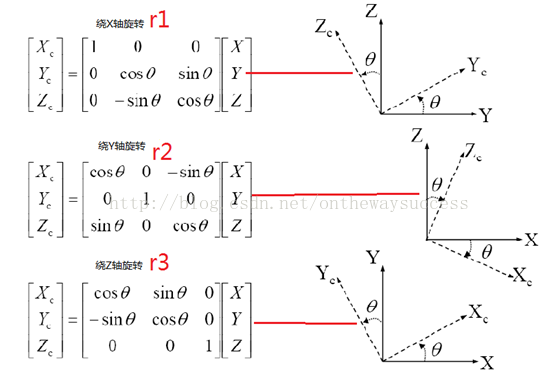
R则为分别绕XYZ三轴旋转的效果之和。如下面所示:
R=r1*r2*r3.其由三个方向的θ控制,故具有三个自由度。
好了,刚体变换就讲完了。大家应该都了解,世界坐标系到摄像机坐标系之间的转换过程了吧。
接下来,让我们看看摄像机坐标下的坐标如何投影到图像坐标系下,最终变为照片中的一个像素。这其中包含两个过程:一是从摄像机坐标到“空间图像坐标”(x,y)所发生的透视投影;二是从“连续图像坐标”到“离散图像坐标”(u,v)。后者我们已经在第一篇博文中解释过。所以在这里,主要介绍一下透视投影。
透视投影(perspective projection): 用中心投影法将形体投射到投影面上,从而获得的一种较为接近视觉效果的单面投影图。有一点像皮影戏。它符合人们心理习惯,即离视点近的物体大,离视点远的物体小,不平行于成像平面的平行线会相交于消隐点(vanish point)。
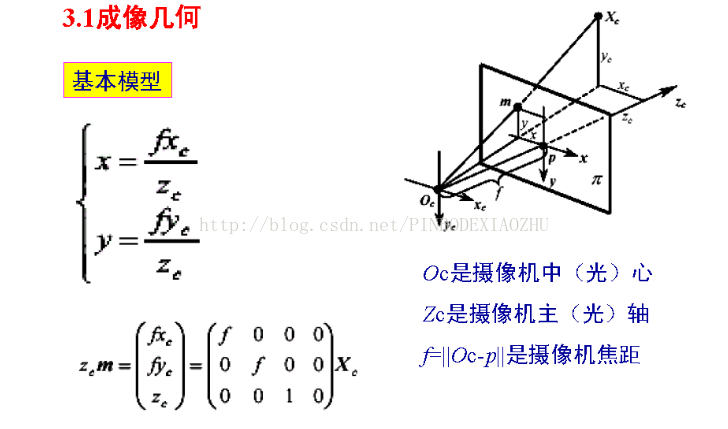
啰嗦这么多,其实大家看看示意图,看看公式,秒懂。
以图中B(XB,YB)点为例,在小孔成像摄像机模型下(几何分析的最常用模型)。这里的f为摄像机的焦距,其属于摄像机的内参数(intrinsic parameter)。其在成像平面上的投影点b(xb,yb)的坐标利用简单的相似三角形比例关系很容易求出:
上面两式也阐明了摄像机坐标与图像坐标之间的透视投影关系。
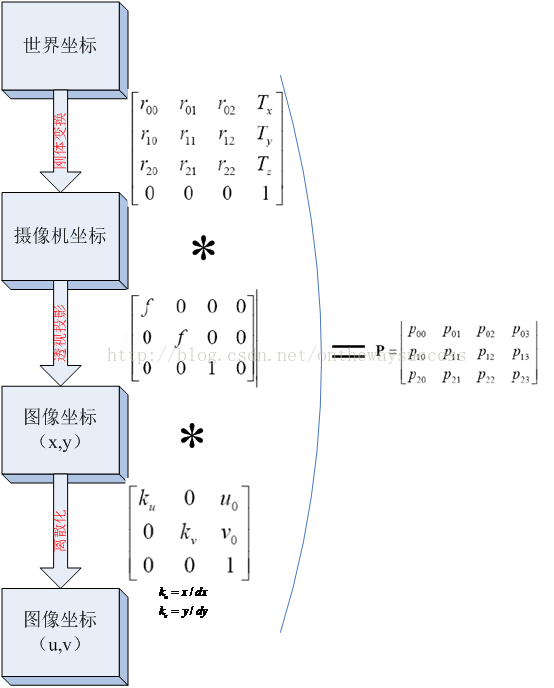
好吧,现在玉米已经把图像坐标与世界坐标之间的这场对话所需经历的三个波折的过程加以了解释。即:刚体变换、透视投影、(x,y)换(u,v)(ps.这个在上一篇博文中讲过)。接下来玉米用一张图把三个过程连接起来。实现从世界坐标(X,Y,Z)到(u,v)之间的转换。让图像坐标与世界坐标直接对话。
下图中的转换关系,都是用齐次坐标表达的,大家会发现这样的表达非常整洁。
其实这张图显示的过程还有一个名字:摄像机模型(camera model)。其实也就是摄像机的几何模型了。
将三者相乘,可以把这三个过程和在一起,写成一个矩阵:
P就是世界坐标到图像坐标的直接联系人,P就表示了一个投影相机,有下面公式:
注意在表示齐次坐标时,需要在符号上面加个小帽子。除去齐次坐标控制位P23,P具有11个自由度。
摄像机模型及其中涉及的坐标系等,是弄清3D重建几何框架的基础。可以把它们视为基本运算关系。后面对于三维重建几何框架的推导,都是要用到三个基本坐标系和摄像机模型的。
到这里玉米就顺利搭建起了图像坐标与世界坐标间的这场对话。如有纰漏还请大家担待,并指正!

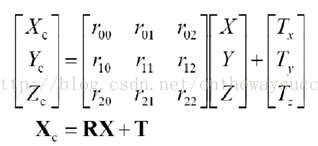
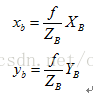
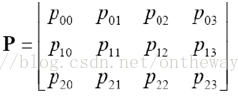
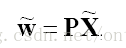









)

)


合并分支的方法与策略)




