本来这周计划写下逻辑回归的学习笔记，但是其中用到了最优化对数似然函数，因此决定先复习下梯度方法和拟牛顿法。本节先从纯数学的角度总结下梯度下降法。

一、柯西-施瓦茨不等式

对于 $\mathbb {R^n}$中的任意两个向量 $\boldsymbol{x}$ 和$\boldsymbol{y}$， 有：

$$|<\boldsymbol{x},\boldsymbol{y}>| \le ||\boldsymbol{x}|| ||\boldsymbol{y}||$$
成立。当且仅当对于某个 $\alpha \in \mathbb{R^n}, 有 x = \alpha y 时，该不等式的等号成立。$

二、梯度下降法

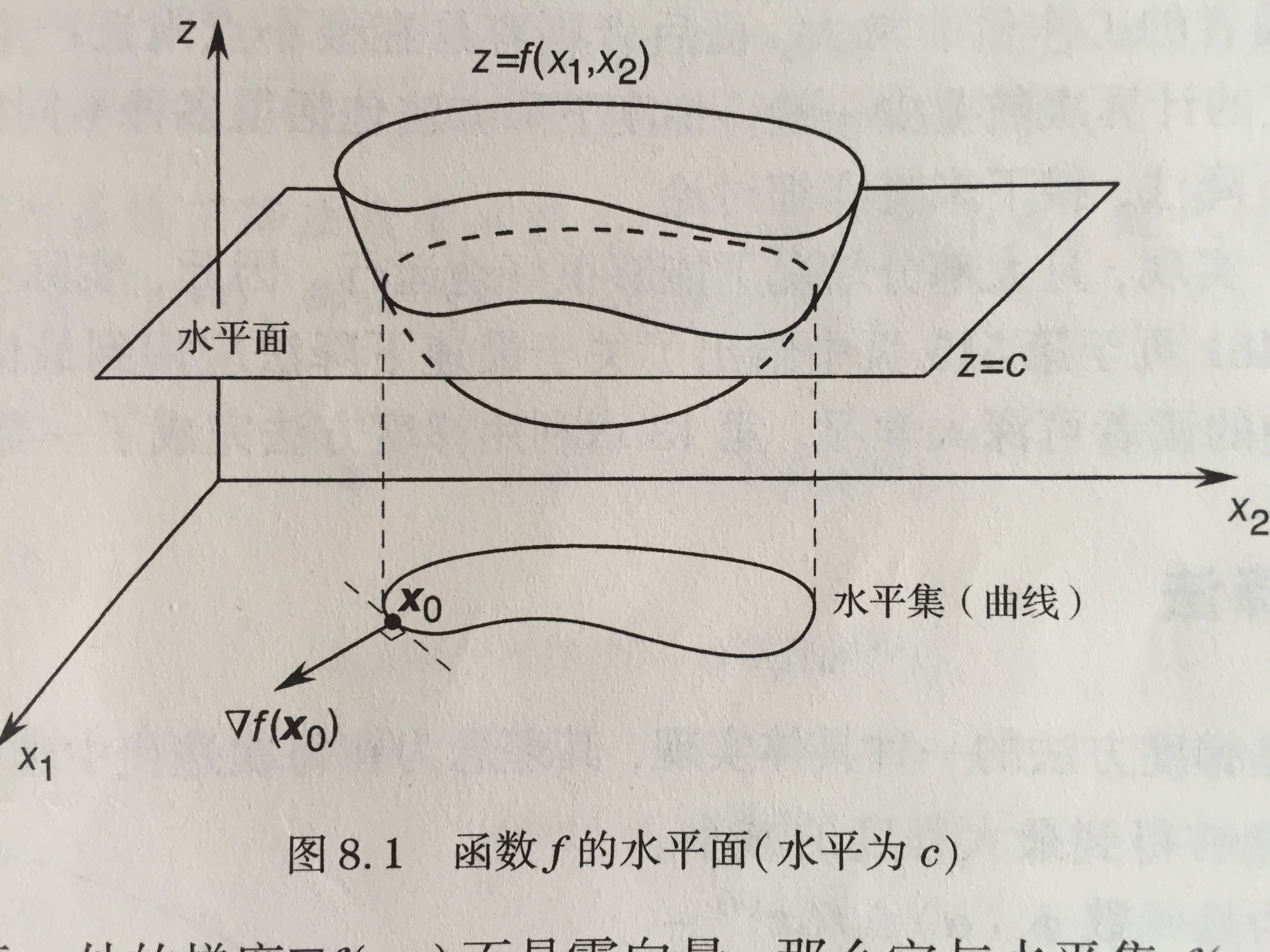
     函数 $f: \mathbb{R^n} \to \mathbb{R}$水平集的概念。水平集是指能够满足$f(x) = c$的所有$x$组成的集合，其中$c$为常数。如下图所示：

     如果函数$f$在$\boldsymbol{x_0}$处的梯度$\triangledown f(x_0)$不是零向量，那么它与水平集$f(x)=c$中任意一条经过$x_0$处的光滑曲线的切向量正交。在梯度方向上，自变量的细微变动，导致的目标函数值的增加幅度要超过其他任意方向。证明如下：函数 $f$在点$x$处，在方向$\boldsymbol{d}$上的增长率为: <▽f(x),d>,||d||=1<script type="math/tex" id="MathJax-Element-50"><\triangledown f( \boldsymbol{x}), \boldsymbol{d}>, ||\boldsymbol{d}|| = \boldsymbol{1}</script>。由柯西-施瓦茨不等式得：

$$\langle \triangledown f( \boldsymbol{x}), \boldsymbol{d}\rangle \le ||\triangledown f( \boldsymbol{x})||$$
若令 $\boldsymbol{d} = \frac{\triangledown f( \boldsymbol{x})}{||\triangledown f( \boldsymbol{x})||}$,则有：
$$\langle \triangledown f( \boldsymbol{x}), \frac{\triangledown f( \boldsymbol{x})}{||\triangledown f( \boldsymbol{x})||} \rangle = ||\triangledown f( \boldsymbol{x})||$$
     因此，可以看出梯度方向 $\triangledown f( \boldsymbol{x})$就是函数 $f$在$\boldsymbol{x}$处增加最快的方向。反之，梯度负方向 $-\triangledown f( \boldsymbol{x})$就是函数 $f$在$\boldsymbol{x}$处减少最快的方向。

     令$\boldsymbol{x^{(0)}}$作为初始搜索点，并沿着梯度负方向构造一个新点$\boldsymbol{x^{(0)}} - \alpha \triangledown f( \boldsymbol{x^{(0)}})$,由泰勒定理可得：

$$f(\boldsymbol{x^{(0)}} - \alpha \triangledown f( \boldsymbol{x^{(0)}})) = f(\boldsymbol{x^{(0)}})-\alpha ||\triangledown f( \boldsymbol{x^{(0)}})||^2+o(\alpha)$$
因此，如果 $\triangledown f( \boldsymbol{x^{(0)}}) \neq \boldsymbol{0}$, 那么当 $\alpha > 0$足够小时，有
$$f(\boldsymbol{x^{(0)}} - \alpha \triangledown f( \boldsymbol{x^{(0)}}))<f(\boldsymbol{x^{(0)}})$$
给定一个搜索点 $\boldsymbol{x^{(k)}}$,由此点出发，根据向量 $-\alpha_k\triangledown f( \boldsymbol{x^{(k)}}))$指定的方向和幅度运动，构造一个新点 $\boldsymbol{x^{(k+1)}}，\alpha_k >0,$称为步长，那么迭代公式如下：
$$\boldsymbol{x^{(k+1)}} = \boldsymbol{x^{(k)}} - \alpha_k\triangledown f( \boldsymbol{x^{(k)}})$$
这称为梯度下降方法。在搜索过程中，梯度不断变化，当接近极小点的时候梯度应该趋于0.可以设置很小的步长，这时计算量比较大，每次梯度都要重新计算；也可以设置很大的步长，这样，计算量会小一些，但是会在极小点附近产生锯齿状的收敛路径。下面会继续总结梯度下降法中的最速下降法。