Word2Vec学习笔记（三）续

三、（续）Skip-gram模型介绍

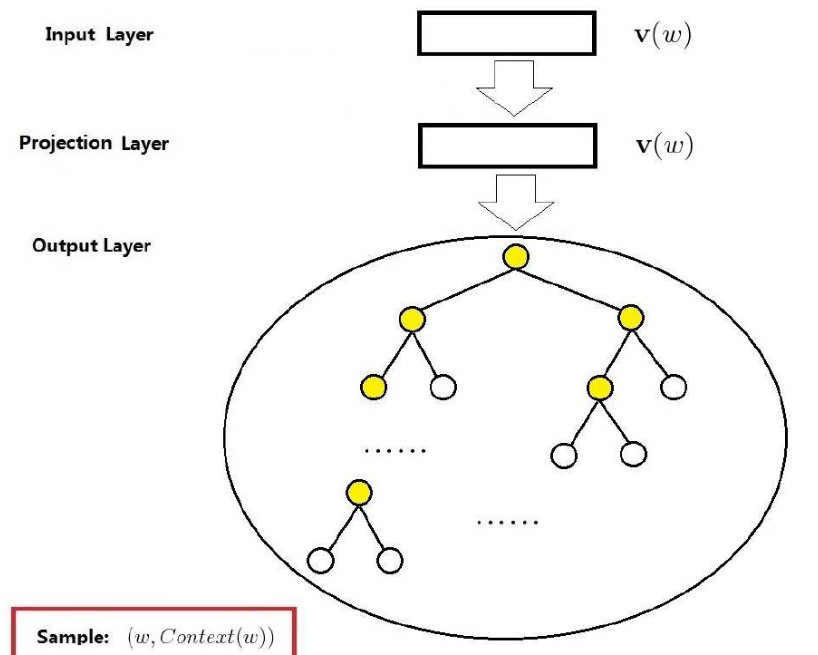
Skip-gram模型并不是和CBOW模型相反的，它们的目的都是计算出词的向量，只不过在作者的论文中给出的图看样子是反的而已。Skip-gram模型是用每个当前词去预测一定范围内除当前词之外前后的词。同样的，此模型也是输出一颗huffman树，如下图所示：此图也借用下图借用
http://blog.csdn.net/itplus/article/details/37969979
Skip-gram模型示意图

Skip-gram模型的目标函数

由于Skip-gram的模型输入是当前词，目的是预测它周围的词，因此，此任务的目标函数如下所示：

L = \sum w \in C log P (c o n t e x t (w) | w)

$\mathcal{L} = \sum_{w \in C} \log P(context(w)|w)$
由于

context(w) $context(w)$ 是一个句子，因此，可以将

P(context(w)|w) $P(context(w)|w)$ 写成如下形式：

P (c o n t e x t (w) | w) = \prod u \in c o n t e x t (w) P (u | w)

$P(context(w)|w) = \prod_{u \in context(w)}P(u|w)$
根据hierarchical softmax的讨论：

P (u | w) = \prod j = 2 l u P (d u j | v (u); θ j - 1)

$P(u|w) = \prod_{j=2}^{l^u}P(d_j^u|v(u); \theta_{j-1})$
那么：最终的目标函数可以写为：

L = \sum w \in C log \prod u \in c o n t e x t (w) \prod j = 2 l u P (d w j | v (u); θ j - 1)

$\mathcal{L} = \sum_{w \in C} \log \prod_{u \in context(w)} \prod_{j=2}^{l^u}P(d_j^w|v(u); \theta_{j-1})$

这里， $\theta, v(w)$ 的更新公式先留着，待推导完再进行补充。
今天推导了一下，其实和上节中的推导差不多，现将推导过程记录一下

L = \sum w \in C log \prod u \in c o n t e x t (w) \prod j = 2 l u P (d w j | v (u); θ j - 1) = \sum w \in C \sum u \in c o n t e x t (w) \sum j = 2 l u log P (d w j | v (u); θ j - 1) = \sum w \in C \sum u \in c o n t e x t (w) \sum j = 2 l u log {[1 - σ (v (w) T θ u j - 1)] d u j σ (v (w) T θ u j - 1)] 1 - d u j} = \sum w \in C \sum u \in c o n t e x t (w) \sum j = 2 l u {d u j log [1 - σ (v (w) T θ u j - 1)] + (1 - d u j) log [σ (v (w) T θ u j - 1)]}

$\mathcal{L} = \sum_{w \in C} \log \prod_{u \in context(w)} \prod_{j=2}^{l^u}P(d_j^w|v(u); \theta_{j-1}) \\ = \sum_{w \in C}\sum_{u \in context(w)} \sum_{j=2}^{l^u} \log P(d_j^w|v(u); \theta_{j-1})\\ = \sum_{w \in C}\sum_{u \in context(w)} \sum_{j=2}^{l^u} \log \{ [1-\sigma(v(w)^T\theta_{j-1}^{u})]^{d_j^u} \sigma(v(w)^T\theta_{j-1}^{u})]^{1-d_j^u} \}\\ =\sum_{w \in C}\sum_{u \in context(w)} \sum_{j=2}^{l^u} \{d_j^u\log [1-\sigma(v(w)^T\theta_{j-1}^{u})] + (1-d_j^u)\log [\sigma(v(w)^T\theta_{j-1}^{u})]\}$
令

f=dujlog[1−σ(v(w)Tθuj−1)]+(1−duj)log[σ(v(w)Tθuj−1)] $f = d_j^u\log [1-\sigma(v(w)^T\theta_{j-1}^{u})] + (1-d_j^u)\log [\sigma(v(w)^T\theta_{j-1}^{u})]$ ,则分别求出

f $f$ 对

θj $\theta_j$ 和

v(w) $v(w)$ 求偏导数：

\partial f \partial θ u j - 1 = [1 - d u j - σ (v (w) T θ u j - 1)] v (w) \partial f \partial v ( w ) = [1 - d u j - σ (v (w) T θ u j - 1)] θ u j - 1

$\frac{\partial{f}}{\partial{\theta_{j-1}^{u}}}=[1-d_j^u-\sigma(v(w)^T\theta_{j-1}^{u})] v(w)\\ \frac{\partial{f}}{\partial{v(w)}} = [1-d_j^u-\sigma(v(w)^T\theta_{j-1}^{u})] \theta_{j-1}^{u}$
那么

θ $\theta$ 和

v(w) $v(w)$ 的更新公式如下：

θ u j - 1 : = θ u j - 1 + η [1 - d u j - σ (v (w) T θ u j - 1)] v (w) v (w) : = v (w) + \sum u \in c o n t e x t (w) \sum j = 2 l u [1 - d u j - σ (v (w) T θ u j - 1)] θ u j - 1

$\theta_{j-1}^{u} :=\theta_{j-1}^{u}+\eta [1-d_j^u-\sigma(v(w)^T\theta_{j-1}^{u})] v(w)\\ v(w):=v(w)+\sum_{u \in context(w)} \sum_{j=2}^{l^u}[1-d_j^u-\sigma(v(w)^T\theta_{j-1}^{u})] \theta_{j-1}^{u}$

Word2Vec 的重点参考文献

Efficient Estimation of Word Representations in Vector Spaceh. http://arxiv.org/pdf/1301.3781v3.pdf
Distributed Representations ofWords and Phrases and their Compositionality. https://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf
Exploiting Similarities among Languages for Machine Translation. http://static.googleusercontent.com/media/research.google.com/zh-CN//pubs/archive/44931.pdf
http://blog.csdn.net/itplus/article/details/37969979
http://www.cnblogs.com/neopenx/p/4571996.html
http://blog.csdn.net/zhoubl668/article/details/24319529

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/576621.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！