三、Hierarchical Softmax模型

3.1 词向量

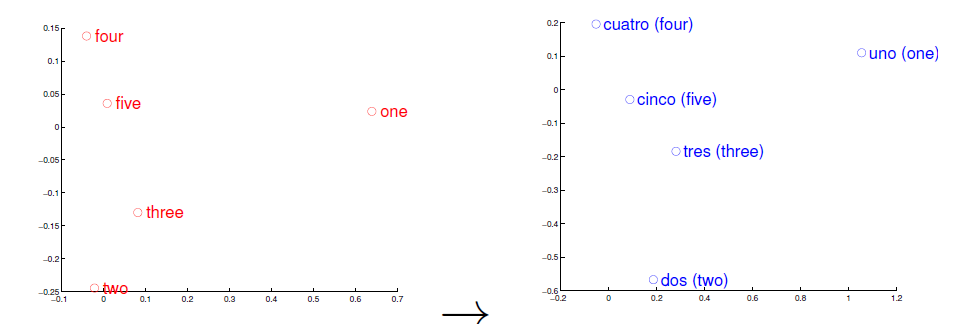
    词向量目前常用的有2种表示方法，One-hot representation 和 distributed representation. 词向量，顾名思义就是将一个词表示为向量的形式，一个词，怎么可以将其表现为向量呢？最简单的就是One-hot representation，它是以词典V中的词的个数作为向量的维度，按照字典序或某种特定的顺序将V排序后，词w的向量可以表示为： $[0, 0, 1, 0, 0 , \dots, 0]$,即词w出现的位置为1，其余均为0. 可以看到，这种方法表示的词向量太过于稀疏，维度太高，会引起维度灾难，而且非常不利于计算词之间的相似度。另一种distributed representation可以解决上述问题，它通过训练将一个词映射为相对于One-hot representation来说一个比较短的向量，它的表示形式类似于：[0.1,0.34,0.673,0.983]。词向量就是将词映射到词典空间中，如下图所示的词向量是两种不同的语言映射。

3.2 CBOW模型和Skip-Gram模型

    CBOW模型很像 feedforward NNLM(A Neural Probabilistic Language Model),feedforward NNLM模型如下所示：

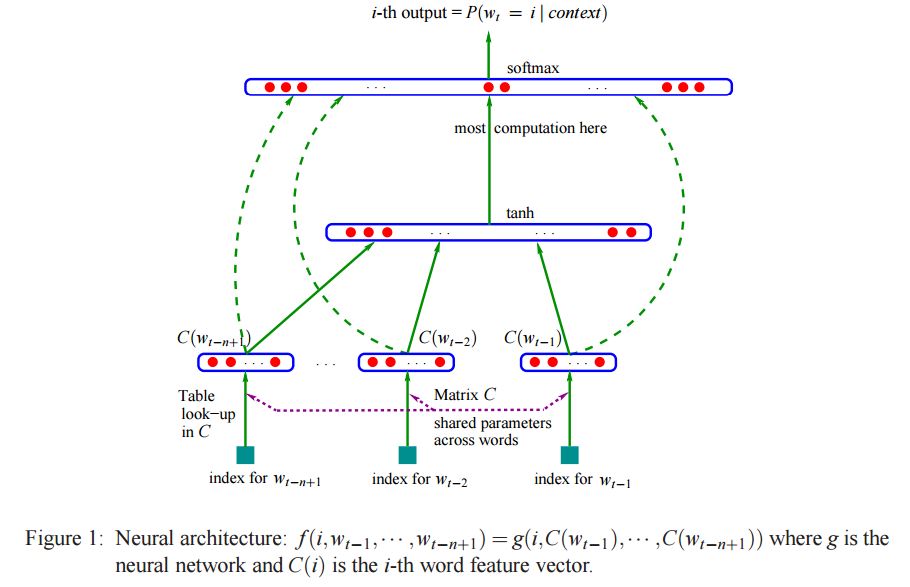
其中C是一个词向量矩阵，首先，将词$w_i$的词向量从C中取出，并且首尾相接组成$\boldsymbol{x}$作为神经网络的第一层输入层，第二层为隐藏层，通过 $d+Hx$ 计算得到。$d$ 是一个偏置项。在此之后，使用 $\tanh$ 作为激活函。第三层输出层，一共有 $|V|$ 个节点，每个节点 $y_i$ 表示下一个词为$i$的未归一化 log 概率。最后使用 softmax 激活函数将输出值 $y$ 归一化成概率。最终，$y$ 的计算公式为：$y = b + Wx + U\tanh(d+Hx)$。
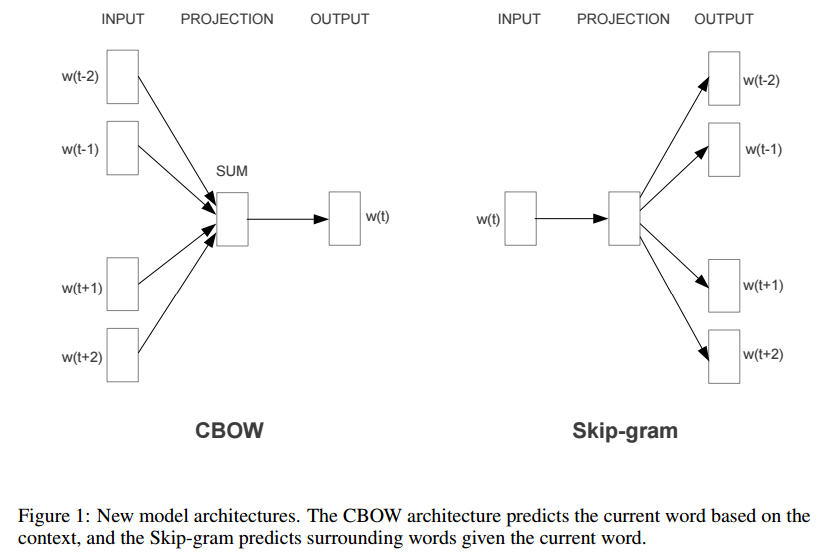
    CBOW将隐藏层移除，投影层不再是词向量的拼接，而是各个词向量相加后取平均作为输入，由上图可以看到，NNLM模型大部分的计算量在输出层上的softmax归一化运算，因此，CBOW为了简化模型，在输出层输出huffman树。CBOW模型根据上下文预测当前词。Skip-gram模型是用每个当前词去预测一定范围内除当前词之外前后的词。并不是有些人说的CBOW的相反版本。论文关于这一点的原文是：we use each current word as an input to a log-linear classifier with continuous projection layer, and predict words within a certain range before and after the current word. 参考 http://arxiv.org/pdf/1301.3781v3.pdf

3.3 CBOW模型的推导

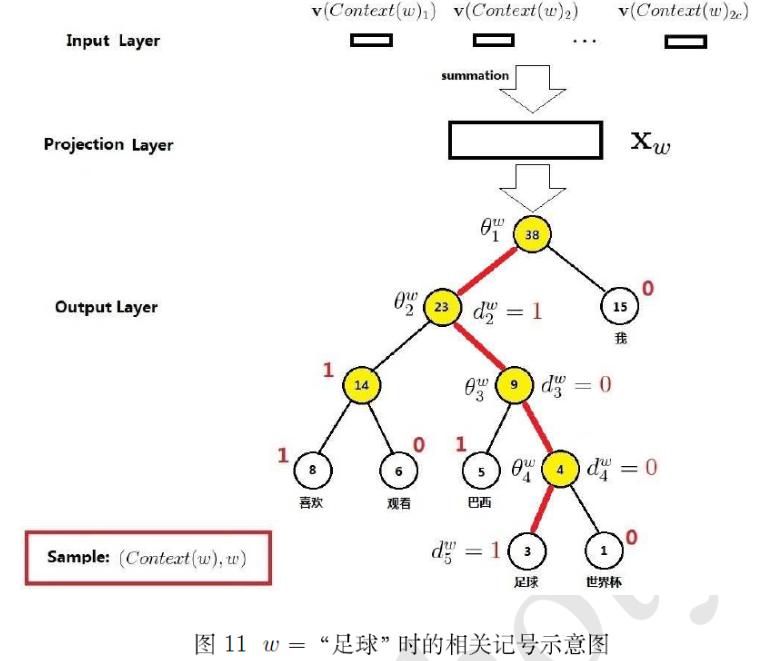
    由于模型的输出是一颗huffman树，其中树的叶子节点表示词，根节点表示权值。CBOW的核心内容是推导出$p(w|context(w))$,其中，$context(w)$由w前后各c个词组成。如下图所示：下图借用
http://blog.csdn.net/itplus/article/details/37969979

1. 由输入层$context(w)$得到投影层向量$\boldsymbol{X_w}$:
   $$\boldsymbol{X_w} = \sum_{i=1}^{2c} \boldsymbol{V}(context(w)_i)$$
   以上$\boldsymbol{V}(context(w)_i)$初始化为$[\frac{-0.5}{M},\frac{0.5}{M}]$,M为向量的维数。
2. 由huffman树的根节点到叶节点，是多个二分类问题。二分类问题一般用logistic回归解决，给出回归函数：
   $$\sigma(z_i) = \frac{1}{1+e^{-z_i}}, 其中，z=\boldsymbol{X_w^T\theta}, 则\\ p(d_i^w|\boldsymbol{X_w^T;\theta_{i-1}})=1-\sigma(z) , d=1\\ p(d_i^w|\boldsymbol{X_w^T;\theta_{i-1}})=\sigma(z) , d=0$$
3. 由以上huffman树的图可知：
   $$p(w|context(w))=\prod_{i=2}^{l^w} p(d_i^w|\boldsymbol{X_w;\theta_{i-1}})=\prod_{i=2}^{l^w}[\sigma(z_{i-1})^{1-d_i^w}(1-\sigma(z_{i-1}))^{d_i^w}]$$
4. 语言模型的目标函数是取如下最大似然函数
   $$\mathcal{L}=\sum_{w \in \mathcal{C}} \log p(w|context(w))\\ =\sum_{w \in \mathcal{C}} \log \prod_{i=2}^{l^w}[\sigma(z_{i-1})^{1-d_i^w}(1-\sigma(z_{i-1}))^{d_i}]\\ =\sum_{w \in \mathcal{C}}\sum_{i=2}^{l^w}[(1-d_i^w)\log\sigma(z_{i-1})+d_i^w \log (1-\sigma(z_{i-1}))]$$
   记以下函数为：
   $$\mathcal{L}(w, i) = (1-d_i^w)\log\sigma(z_{i-1})+d_i^w \log (1-\sigma(z_{i-1})) \\ $$
   将z_i代入得：
   $$\mathcal{L}(w, i) = (1-d_i^w)\log\sigma(\boldsymbol{X_w^T\theta_{i-1}})+d_i^w \log (1-\sigma(\boldsymbol{X_w^T\theta_{i-1}})$$
5. 求函数$\mathcal{L}(w, i)$对$w$和$\theta_{i-1}$求偏导数：
   $$\frac{\partial \mathcal{L}(w, i)}{\partial \boldsymbol{X_w}} = (1-d_i^w-\frac{1}{1+e^{\boldsymbol{-X_w^T\theta_i-1}}})\boldsymbol{\theta_{i-1}}\\ \frac{\partial \mathcal{L}(w, i)}{\partial \boldsymbol{\theta_{i-1}}} = (1-d_i^w-\frac{1}{1+e^{\boldsymbol{-X_w^T\theta_i-1}}})\boldsymbol{X_w^T}$$
6. 那么，参数$\theta_{i-1}$的更新公式如下所示：
   $$\theta_{i-1} := \theta_{i-1} + \eta (1-d_i^w-\frac{1}{1+e^{\boldsymbol{-X_w^T\theta_i-1}}})\boldsymbol{X_w^T}$$
   我们的目的是求每个词的词向量，那么，给出词向量的更新公式：对于每个$w \in context(w)$，都有：
   $$v(w):=v(w)+\eta \sum_{i=2}^{l_w}(1-d_i^w-\frac{1}{1+e^{\boldsymbol{-X_w^T\theta_i-1}}})\boldsymbol{\theta_{i-1}}$$