训练完(稀疏)自编码器,我们还想把这自编码器学到的函数可视化出来,好弄明白它到底学到了什么。我们以在10×10图像(即n=100)上训练自编码器为例。在该自编码器中,每个隐藏单元i对如下关于输入的函数进行计算:
我们将要可视化的函数,就是上面这个以2D图像为输入、并由隐藏单元i计算出来的函数。它是依赖于参数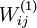 的(暂时忽略偏置项bi)。需要注意的是,
的(暂时忽略偏置项bi)。需要注意的是,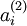 可看作输入
可看作输入 的非线性特征。不过还有个问题:什么样的输入图像
的非线性特征。不过还有个问题:什么样的输入图像 可让
可让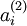 得到最大程度的激励?(通俗一点说,隐藏单元
得到最大程度的激励?(通俗一点说,隐藏单元 要找个什么样的特征?)。这里我们必须给
要找个什么样的特征?)。这里我们必须给 加约束,否则会得到平凡解。若假设输入有范数约束
加约束,否则会得到平凡解。若假设输入有范数约束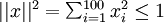 ,则可证(请读者自行推导)令隐藏单元
,则可证(请读者自行推导)令隐藏单元 得到最大激励的输入应由下面公式计算的像素
得到最大激励的输入应由下面公式计算的像素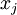 给出(共需计算100个像素,j=1,…,100):
给出(共需计算100个像素,j=1,…,100):
当我们用上式算出各像素的值、把它们组成一幅图像、并将图像呈现在我们面前之时,隐藏单元 所追寻特征的真正含义也渐渐明朗起来。
所追寻特征的真正含义也渐渐明朗起来。
假如我们训练的自编码器有100个隐藏单元,可视化结果就会包含100幅这样的图像——每个隐藏单元都对应一幅图像。审视这100幅图像,我们可以试着体会这些隐藏单元学出来的整体效果是什么样的。
当我们对稀疏自编码器(100个隐藏单元,在10X10像素的输入上训练 )进行上述可视化处理之后,结果如下所示:
上图的每个小方块都给出了一个(带有有界范数 的)输入图像 ,它可使这100个隐藏单元中的某一个获得最大激励。我们可以看到,不同的隐藏单元学会了在图像的不同位置和方向进行边缘检测。
,它可使这100个隐藏单元中的某一个获得最大激励。我们可以看到,不同的隐藏单元学会了在图像的不同位置和方向进行边缘检测。
显而易见,这些特征对物体识别等计算机视觉任务是十分有用的。若将其用于其他输入域(如音频),该算法也可学到对这些输入域有用的表示或特征。
中英文对照
- 可视化 Visualizing
- 自编码器 Autoencoder
- 隐藏单元 hidden unit
- 非线性特征 non-linear feature
- 激励 activate
- 平凡解 trivial answer
- 范数约束 norm constrained
- 稀疏自编码器 sparse autoencoder
- 有界范数 norm bounded
- 输入域 input domains
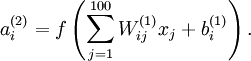
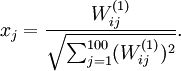

主成分分析)

线性回归)
支持向量机)

图的操作)

最短路径)

条件最短路径)
)
线性规划问题)

最小生成树)
关键路径法)




探讨)