主成分分析（Principal Components Analysis，PCA）是一种数据降维技术，通过正交变换将一组相关性高的变量转换为较少的彼此独立、互不相关的变量，从而减少数据的维数。

---

1、数据降维

1.1 为什么要进行数据降维？

为什么要进行数据降维？降维的好处是以略低的精度换取问题的简化。

人们在研究问题时，为了全面、准确地反映事物的特征及其发展规律，往往要考虑很多相关指标的变化和影响。尤其在数据挖掘和分析工作中，前期收集数据阶段总是尽量收集能够获得的各种数据，能收尽收，避免遗漏。多变量、大样本的数据为后期的研究和应用提供了丰富的信息，从不同角度反映了问题的特征和信息，但也给数据处理和分析工作带来了很多困难。

为了避免遗漏信息需要获取尽可能多的特征变量，但是过多的变量又加剧了问题的复杂性。由于各种变量都是对同一事物的反映，变量之间经常会存在一定的相关性，这就造成大量的信息重复、重叠，有时会淹没甚至扭曲事物的真正特征与内在规律。因此，我们希望数据分析中涉及的变量较少，而得到的信息量又较多。这就需要通过降维方法，在减少需要分析的变量数量的同时，尽可能多的保留众多原始变量所包含的有效信息。

变量之间具有一定的相关关系，意味着相关变量所反映的信息有一定程度的重叠，就有可能用较少的综合指标聚合、反映众多原始变量所包含的全部信息或主要信息。 因此，需要研究特征变量之间的相关性、相似性，以减少特征变量的数量，便于分析影响系统的主要因素。例如，对学生的评价指标有很多，作业、考勤、活动、奖惩、考试、考核，根据各种指标的关联度和相似性，最终可以聚合为德智体美等几个主要的类别指标反映众多指标中大部分信息。
　　
降维方法可以从事物之间错综复杂的关系中找出一些主要因素，从而能有效利用大量统计数据进行定量分析，解释变量之间的内在关系，得到对事物特征及其发展规律的一些深层次的启发。

欢迎关注 Youcans 原创系列，每周更新数模笔记

Python数模笔记-PuLP库
Python数模笔记-StatsModels统计回归
Python数模笔记-Sklearn
Python数模笔记-NetworkX
Python数模笔记-模拟退火算法

1.2 常用的降维思想和方法

降维的数学本质是将高维特征空间映射到低维特征空间，有线性映射和非线性映射两类主要方法。

线性映射方法主要有主成分分析（PCA）和线性判别函数（LDA）。主成分分析（PCA）的思想是按均方误差损失最小化原则，将高维原始空间变换到低维特征向量空间。线性判别函数（LDA）的思想是向线性判别超平面的法向量上投影，使得区分度最大（高内聚，低耦合） 。

非线性映射方法主要有：基于核的非线性降维， 将高维向量的内积转换成低维的核函数表示，如核主成分分析（KPCA）、核线性判别函数（KLDA） ；二维化和张量化， 将数据映射到二维空间上，如二维主成分分析（2DPCA）、二维线性判别分析（2DLDA）、二维典型相关分析（2DCCA）；流形学习方法， 从高维采样数据中恢复低维流形结构并求出相应的嵌入映射，如等距映射 （ISOMap） ， 拉普拉斯特征映射 （LE）， 局部线性嵌入 （LPP）。本质上，非线性映射的思想和算法与神经网络是相通的。

此外，还可以通过聚类分析、神经网络方法进行数据降维。

1.3 SKlearn 中的降维分析方法

SKlearn 工具包提供了多种降维分析方法。

• 主成分分析
  • decomposition.PCA　　主成分分析
  • decomposition.IncrementalPCA　　增量主成分分析
  • decomposition.KernelPCA　　核主成分分析
  • decomposition.SparsePCA　　稀疏主成分分析
  • decomposition.MiniBatchSparsePCA　　小批量稀疏主成分分析
  • decomposition.TruncatedSVD　　截断奇异值分解
• 字典学习
  • decomposition.DictionaryLearning　　字典学习
  • decomposition.MiniBatchDictionaryLearning　　小批量字典学习
  • decomposition.dict_learning　　字典学习用于矩阵分解
  • decomposition.dict_learning_online　　在线字典学习用于矩阵分解
• 因子分析
  • decomposition.FactorAnalysis　　因子分析（FA）
• 独立成分分析
  • decomposition.FastICA　　快速独立成分分析
• 非负矩阵分解
  • decomposition.NMF　　非负矩阵分解
• 隐式狄利克莱分布
  • decomposition.LatentDirichletAllocation　　在线变分贝叶斯算法（隐式狄利克莱分布）

---

2、主成分分析（PCA）方法

2.1 基本思想和原理

主成分分析是最基础数据降维方法，它只需要特征值分解，就可以对数据进行压缩、去噪，应用十分广泛。

主成分分析的目的是减少数据集变量数量，同时要保留尽可能多的特征信息；方法是通过正交变换将原始变量组转换为数量较少的彼此独立的特征变量，从而减少数据集的维数。

主成分分析方法的思想是，将高维特征（n维）映射到低维空间（k维）上，新的低维特征是在原有的高维特征基础上通过线性组合而重构的，并具有相互正交的特性，即为主成分。

通过正交变换构造彼此正交的新的特征向量，这些特征向量组成了新的特征空间。将特征向量按特征值排序后，样本数据集中所包含的全部方差，大部分就包含在前几个特征向量中，其后的特征向量所含的方差很小。因此，可以只保留前 k个特征向量，而忽略其它的特征向量，实现对数据特征的降维处理。

主成分分析方法得到的主成分变量具有几个特点：（1）每个主成分变量都是原始变量的线性组合；（2）主成分的数目大大少于原始变量的数目；（3）主成分保留了原始变量的绝大多数信息；（4）各主成分变量之间彼此相互独立。

2.2 算法步骤

主成分分析的基本步骤是：对原始数据归一化处理后求协方差矩阵，再对协方差矩阵求特征向量和特征值；对特征向量按特征值大小排序后，依次选取特征向量，直到选择的特征向量的方差占比满足要求为止。

算法的基本流程如下：

• （1）归一化处理，数据减去平均值；
• （2）通过特征值分解，计算协方差矩阵；
• （3）计算协方差矩阵的特征值和特征向量；
• （4）将特征值从大到小排序；
• （5）依次选取特征值最大的k个特征向量作为主成分，直到其累计方差贡献率达到要求；
• （6）将原始数据映射到选取的主成分空间，得到降维后的数据。

在算法实现的过程中，SKlearn 工具包针对实际问题的特殊性，又发展了各种改进算法，例如：

• 增量主成分分析：针对大型数据集，为了解决内存限制问题，将数据分成多批，通过增量方式逐步调用主成分分析算法，最终完成整个数据集的降维。
• 核主成分分析：针对线性不可分的数据集，使用非线性的核函数把样本空间映射到线性可分的高维空间，然后在这个高维空间进行主成分分析。
• 稀疏主成分分析：针对主成分分析结果解释性弱的问题，通过提取最能重建数据的稀疏分量， 凸显主成分中的主要组成部分，容易解释哪些原始变量导致了样本之间的差异。

2.3 优点和缺点

主成分分析方法的主要优点是：
　　1）仅以方差衡量信息量，不受数据集以外的因素影响；　
　　2）各主成分之间正交，可消除原始数据各变量之间的相互影响；
　　3）方法简单，易于实现。

主成分分析方法的主要缺点是：
　　1）各个主成分的含义具有模糊，解释性弱，通常只有信息量而无实际含义；
　　2）在样本非正态分布时得到的主成分不是最优的，因此特殊情况下方差小的成分也可能含有重要信息。

---

3、SKlearn 中的主成分分析（PCA） 方法

3.1 PCA 算法（decomposition.PCA）

sklearn.decomposition.PCA 类是 PCA算法的具体实现，官网介绍详见：https://scikit-learn.org/stable/modules/decomposition.html#principal-component-analysis-pca

sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)

class sklearn.decomposition.PCA(n_components=None, *, copy=True, whiten=False, svd_solver=‘auto’, tol=0.0, iterated_power=‘auto’, random_state=None)

PCA 类的主要参数：

• n_components: int,float　　n 为正整数，指保留主成分的维数；n 为 (0,1] 范围的实数时，表示主成分的方差和所占的最小阈值。
• whiten：bool, default=False　　是否对降维后的主成分变量进行归一化。默认值 False。
• svd_solver：{‘auto’, ‘full’, ‘arpack’, ‘randomized’}　　指定奇异值分解SVD的算法。‘full’ 调用 scipy库的 SVD；'arpack’调用scipy库的 sparse SVD；‘randomized’ SKlearn的SVD，适用于数据量大、变量维度多、主成分维数低的场景。默认值 ‘auto’。

PCA 类的主要属性：

• components_： 　　方差最大的 n-components 个主成分
• explained_variance_：　　各个主成分的方差值
• explained_variance_ratio_：　　各个主成分的方差值占主成分方差和的比例

PCA 类的主要方法：

• fit(X,y=None)　　表示用数据 X 训练PCA模型
  fit() 是scikit-learn中的通用方法，实现训练、拟合的步骤。PCA是无监督学习，y=None。
• fit_transform(X)　　表示用数据 X 训练PCA模型，并返回降维后的数据
• transform(X)　　将数据 X 转换成降维后的数据，用训练好的 PCA模型对新的数据集进行降维。
• inverse_transform()　　将降维后的数据转换成原始数据

3.2 decomposition.PCA 使用例程

from sklearn.decomposition import PCA  # 导入 sklearn.decomposition.PCA 类
import numpy as np  # Youcans， XUPTX = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
modelPCA = PCA(n_components=2)  # 建立模型，设定保留主成分数 K=2
modelPCA.fit(X)  # 用数据集 X 训练 模型 modelPCA
print(modelPCA.n_components_)  # 返回 PCA 模型保留的主成份个数
# 2
print(modelPCA.explained_variance_ratio_)  # 返回 PCA 模型各主成份占比
# [0.9924 0.0075]  # print 显示结果
print(modelPCA.singular_values_) # 返回 PCA 模型各主成份的奇异值
# [6.3006 0.5498]  # print 显示分类结果X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
modelPCA2 = PCA(n_components=0.9) # 建立模型，设定主成份方差占比 0.9
# 用数据集 X 训练 模型 modelPCA2，并返回降维后的数据
Xtrans = modelPCA2.fit_transform(X)
print(modelPCA2.n_components_)  # 返回 PCA 模型保留的主成份个数
# 1
print(modelPCA2.explained_variance_ratio_)  # 返回 PCA 模型各主成份占比
# [0.9924]  # print 显示结果
print(modelPCA2.singular_values_)  # 返回 PCA 模型各主成份占比
# [6.3006]  # print 显示结果
print(Xtrans)  # 返回降维后的数据 Xtrans
# [[1.3834], [2.2219], [3.6053], [-1.3834], [-2.2219], [-3.6053]]
# = 关注 Youcans，分享原创系列 https://blog.csdn.net/youcans =

注意：建立模型时，PCA(n_components=2) 中的 n_components为正整数，表示设定保留的主成份维数为 2；PCA(n_components=0.9) 中的 n_components 为 (0,1] 的小数，表示并不直接设定保留的主成份维数，而是设定保留的主成份应满足其方差和占比 >0.9。

3.3 改进算法：增量主成分分析（decomposition.IncrementalPCA）

对于样本集巨大的问题，例如样本量大于 10万、特征变量大于100，PCA 算法耗费的内存很大，甚至无法处理。　　　
　　class sklearn.decomposition.IncrementalPCA 类是增量主成分分析算法的具体实现，官网介绍详见：https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.IncrementalPCA.html#sklearn.decomposit

class sklearn.decomposition.IncrementalPCA(n_components=None, *, whiten=False, copy=True, batch_size=None)

主要参数：
inverse_transform()　　将降维后的数据转换成原始数据

IncrementalPCA 的使用例程如下：

# Demo of sklearn.decomposition.IncrementalPCAfrom sklearn.datasets import load_digits
from sklearn.decomposition import IncrementalPCA, PCA
from scipy import sparse  # Youcans， XUPTX, _ = load_digits(return_X_y=True)
print(type(X))  # <class 'numpy.ndarray'>
print(X.shape)      # (1797, 64)modelPCA = PCA(n_components=6)  # 建立模型，设定保留主成分数 K=6
modelPCA.fit(X)  # 用数据集 X 训练 模型 modelPCA
print(modelPCA.n_components_)  # 返回 PCA 模型保留的主成份个数
# 6
print(modelPCA.explained_variance_ratio_)  # 返回 PCA 模型各主成份占比
# [0.1489 0.1362 0.1179 0.0841 0.0578 0.0492]
print(sum(modelPCA.explained_variance_ratio_))  # 返回 PCA 模型各主成份占比
# 0.5941
print(modelPCA.singular_values_) # 返回 PCA 模型各主成份的奇异值
# [567.0066  542.2518 504.6306 426.1177 353.3350 325.8204]# let the fit function itself divide the data into batches
Xsparse = sparse.csr_matrix(X)  # 压缩稀疏矩阵，并非 IPCA 的必要步骤
print(type(Xsparse))  # <class 'scipy.sparse.csr.csr_matrix'>
print(Xsparse.shape)  # (1797, 64)
modelIPCA = IncrementalPCA(n_components=6, batch_size=200)
modelIPCA.fit(Xsparse)  # 训练模型 modelIPCA
print(modelIPCA.n_components_)  # 返回 PCA 模型保留的主成份个数
# 6
print(modelIPCA.explained_variance_ratio_)  # 返回 PCA 模型各主成份占比
# [0.1486 0.1357 0.1176 0.0838 0.0571 0.0409]
print(sum(modelIPCA.explained_variance_ratio_))  # 返回 PCA 模型各主成份占比
# 0.5838
print(modelIPCA.singular_values_) # 返回 PCA 模型各主成份的奇异值
#[566.4544 541.334 504.0643 425.3197 351.1096 297.0412]
# = 关注 Youcans，分享原创系列 https://blog.csdn.net/youcans =

本例程调用了 SKlearn内置的数据集 .datasets.load_digits，并给出了 PCA 算法与 IPCA 算法的对比，两种算法的结果非常接近，说明 IPCA 的性能降低很小。

3.4 改进算法：核主成分分析（decomposition.KernelPCA）

对于线性不可分的数据集，使用非线性的核函数可以把样本空间映射到线性可分的高维空间，然后在这个高维空间进行主成分分析。

class sklearn.decomposition.KernelPCA 类是算法的具体实现，官网介绍详见：https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.KernelPCA.html#sklearn.decomposition.KernelPCA

class sklearn.decomposition.KernelPCA(n_components=None, *, kernel=‘linear’, gamma=None, degree=3, coef0=1, kernel_params=None, alpha=1.0, fit_inverse_transform=False, eigen_solver=‘auto’, tol=0, max_iter=None, remove_zero_eig=False, random_state=None, copy_X=True, n_jobs=None)

KernelPCA 的使用例程如下：

# Demo of sklearn.decomposition.KernelPCAfrom sklearn.datasets import load_iris  # Youcans， XUPT
from sklearn.decomposition import KernelPCA, PCA
import matplotlib.pyplot as plt
import numpy as npX, y = load_iris(return_X_y=True)
print(type(X))  # <class 'numpy.ndarray'>modelPCA = PCA(n_components=2)  # 建立模型，设定保留主成分数 K=2
Xpca = modelPCA.fit_transform(X)  # 用数据集 X 训练 模型 modelKPCAmodelKpcaP = KernelPCA(n_components=2, kernel='poly') # 建立模型，核函数：多项式
XkpcaP = modelKpcaP.fit_transform(X)  # 用数据集 X 训练 模型 modelKPCAmodelKpcaR = KernelPCA(n_components=2, kernel='rbf') # 建立模型，核函数：径向基函数
XkpcaR = modelKpcaR.fit_transform(X)  # 用数据集 X 训练 模型 modelKPCAmodelKpcaS = KernelPCA(n_components=2, kernel='cosine') # 建立模型，核函数：余弦函数
XkpcaS = modelKpcaS.fit_transform(X)  # 用数据集 X 训练 模型 modelKPCAfig = plt.figure(figsize=(8,6))
ax1 = fig.add_subplot(2,2,1)
ax2 = fig.add_subplot(2,2,2)
ax3 = fig.add_subplot(2,2,3)
ax4 = fig.add_subplot(2,2,4)
for label in np.unique(y):position = y == labelax1.scatter(Xpca[position, 0], Xpca[position, 1], label='target=%d' % label)ax1.set_title('PCA')ax2.scatter(XkpcaP[position, 0], XkpcaP[position, 1], label='target=%d' % label)ax2.set_title('kernel= Poly')ax3.scatter(XkpcaR[position, 0], XkpcaR[position, 1], label='target=%d' % label)ax3.set_title('kernel= Rbf')ax4.scatter(XkpcaS[position, 0], XkpcaS[position, 1], label='target=%d' % label)ax4.set_title('kernel= Cosine')
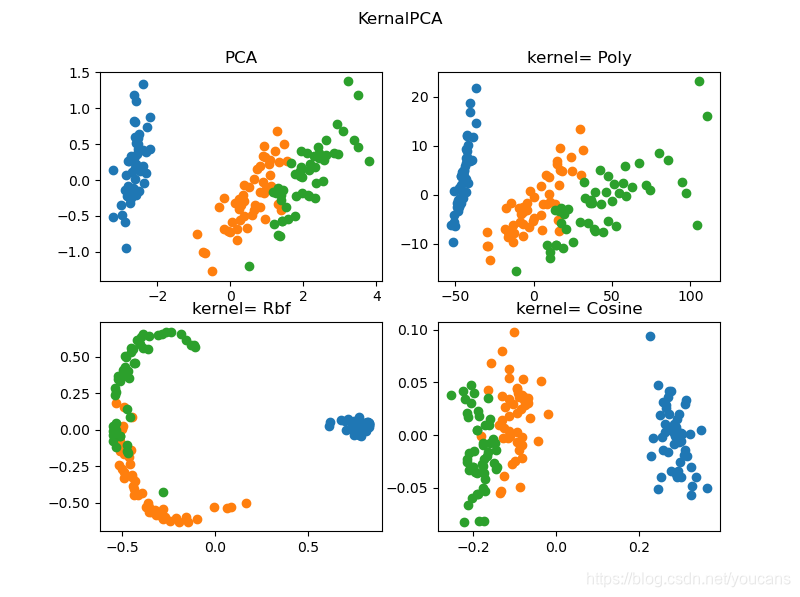
plt.suptitle("KernalPCA (Youcans,XUPT)")
plt.show()
# = 关注 Youcans，分享原创系列 https://blog.csdn.net/youcans =

本例程调用了 SKlearn内置的数据集 .datasets.load_iris，并给出了 PCA 算法与 3种核函数的KernelPCA 算法的对比，结果如下图所示。不同算法的降维后映射到二维平面的结果有差异，进一步的讨论已经超出本文的内容。

---

版权说明：
本文内容及例程为作者原创，并非转载书籍或网络内容。
本文中案例问题来自：SciKit-learn 官网：https://scikit-learn.org/stable/index.html

YouCans 原创作品
Copyright 2021 YouCans, XUPT
Crated：2021-05-10

欢迎关注 Youcans 原创系列，每周更新数模笔记

Python数模笔记-PuLP库（1）线性规划入门
Python数模笔记-PuLP库（2）线性规划进阶
Python数模笔记-PuLP库（3）线性规划实例
Python数模笔记-StatsModels 统计回归（1）简介
Python数模笔记-StatsModels 统计回归（2）线性回归
Python数模笔记-StatsModels 统计回归（3）模型数据的准备
Python数模笔记-StatsModels 统计回归（4）可视化
Python数模笔记-Sklearn （1）介绍
Python数模笔记-Sklearn （2）聚类分析
Python数模笔记-Sklearn （3）主成分分析
Python数模笔记-Sklearn （4）线性回归
Python数模笔记-Sklearn （5）支持向量机
Python数模笔记-模拟退火算法（1）多变量函数优化
Python数模笔记-模拟退火算法（2）约束条件的处理
Python数模笔记-模拟退火算法（3）整数规划问题
Python数模笔记-模拟退火算法（4）旅行商问题