矢量化编程

当使用学习算法时，一段更快的代码通常意味着项目进展更快。例如，如果你的学习算法需要花费20分钟运行完成，这意味着你每个小时能“尝试”3个新主意。但是假如你的程序需要20个小时来运行，这意味着你一天只能“尝试”一个新主意，因为你需要花费这么长时间来等待程序的反馈。对于后者，假如你可以提升代码的效率让其只需要运行10个小时，那么你的效率差不多提升一倍。

矢量化编程是提高算法速度的一种有效方法。为了提升特定数值运算操作（如矩阵相乘、矩阵相加、矩阵-向量乘法等）的速度，数值计算和并行计算的研究人员已经努力了几十年。矢量化编程的思想就是尽量使用这些被高度优化的数值运算操作来实现我们的学习算法。

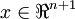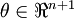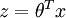例如，假设 $x \in \Re^{n+1}$ 和 $\textstyle \theta \in \Re^{n+1}$ 为向量，需要计算 $\textstyle z = \theta^Tx$ ，那么可以按以下方式实现（使用Matlab）：

z = 0;
for i=1:(n+1),z = z + theta(i) * x(i);
end;

或者可以更加简单的写为：

z = theta' * x;

第二段程序代码不仅简单，而且运行速度更快。

通常，一个编写Matlab/Octave程序的诀窍是：

代码中尽可能避免显式的for循环。

上面的第一段代码使用了一个显式的for循环。通过不使用for循环实现相同功能，可以显著提升运行速度。对Matlab/Octave代码进行矢量化的工作很大一部分集中在避免使用for循环上，因为这可以使得Matlab/Octave更多地利用代码中的并行性，同时其解释器的计算开销更小。

关于编写代码的策略，开始时你会觉得矢量化代码更难编写、阅读和调试，但你需要在编码和调试的便捷性与运行时间之间做个权衡。因此，刚开始编写程序的时候，你可能会选择不使用太多矢量化技巧来实现你的算法，并验证它是否正确（可能只在一个小问题上验证）。在确定它正确后，你可以每次只矢量化一小段代码，并在这段代码之后暂停，以验证矢量化后的代码计算结果和之前是否相同。最后，你会有望得到一份正确的、经过调试的、矢量化且有效率的代码。

一旦对矢量化常见的方法和技巧熟悉后，你将会发现对代码进行矢量化通常并不太费劲。矢量化可以使你的代码运行的更快，而且在某些情况下，还简化了你的代码。