逻辑回归的向量化实现样例
我们想用批量梯度上升法对logistic回归分析模型进行训练,其模型如下:
让我们遵从公开课程视频与CS229教学讲义的符号规范,设 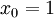 ,于是
,于是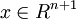 ,
,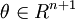 ,
, 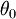 为截距。假设我们有m个训练样本{(
为截距。假设我们有m个训练样本{(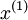 ,
,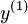 ) ,...,(
) ,...,(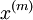 ,
,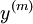 )},而批量梯度上升法的更新法则是:
)},而批量梯度上升法的更新法则是: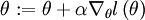 ,这里的
,这里的 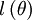 是对数似然函数,
是对数似然函数,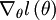 是其导函数。
是其导函数。
[注:下文的符号规范与<公开课程视频>或<教学讲义CS229:机器学习>中的相同,详细内容可以参见公开课程视频或教学讲义#1 http://cs229.stanford.edu/]
于是,我们需要如下计算梯度:
我们用Matlab/Octave风格变量x表示输入数据构成的样本矩阵,x(:,i)代表第 i个训练样本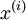 ,x(j,i)就代表
,x(j,i)就代表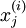 (译者注:第i个训练样本向量的第j个元素)。同样,用Matlab/Octave风格变量y表示由训练样本集合的全体类别标号所构成的行向量,则该向量的第i个元素y(i)就代表上式中的
(译者注:第i个训练样本向量的第j个元素)。同样,用Matlab/Octave风格变量y表示由训练样本集合的全体类别标号所构成的行向量,则该向量的第i个元素y(i)就代表上式中的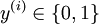 。(注意这里跟公开课程视频及CS229的符号规范不同,矩阵x按列而不是按行存放输入训练样本,同样,
。(注意这里跟公开课程视频及CS229的符号规范不同,矩阵x按列而不是按行存放输入训练样本,同样,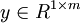 是行向量而不是列向量。)
是行向量而不是列向量。)
以下是梯度运算代码的一种实现,非常恐怖,速度极慢:
% 代码1 grad = zeros(n+1,1); for i=1:m,h = sigmoid(theta'*x(:,i));temp = y(i) - h; for j=1:n+1,grad(j) = grad(j) + temp * x(j,i); end; end;
嵌套的for循环语句使这段代码的运行非常缓慢。以下是更典型的实现方式,它对算法进行部分向量化,带来更优的执行效率:
% 代码2 grad = zeros(n+1,1); for i=1:m,grad = grad + (y(i) - sigmoid(theta'*x(:,i)))* x(:,i); end;
但是,或许可以向量化得更彻底些。如果去除for循环,我们就可以显著地改善代码执行效率。特别的,假定b是一个列向量,A是一个矩阵,我们用以下两种方式来计算A*b:
% 矩阵-向量乘法运算的低效代码 grad = zeros(n+1,1); for i=1:m,grad = grad + b(i) * A(:,i); % 通常写法为A(:,i)*b(i) end;% 矩阵-向量乘法运算的高效代码 grad = A*b;
我们看到,代码2是用了低效的for循环语句执行梯度上升(译者注:原文是下降)运算,将b(i)看成(y(i) - sigmoid(theta'*x(:,i))),A看成x,我们就可以使用以下高效率的代码:
% 代码3 grad = x * (y- sigmoid(theta'*x));
这里我们假定Matlab/Octave的sigmoid(z)函数接受一个向量形式的输入z,依次对输入向量的每个元素施行sigmoid函数,最后返回运算结果,因此sigmoid(z)的输出结果是一个与z有相同维度的向量。
当训练数据集很大时,最终的实现(译者注:代码3)充分发挥了Matlab/Octave高度优化的数值线性代数库的优势来进行矩阵-向量操作,因此,比起之前代码要高效得多。
想采用向量化实现并非易事,通常需要周密的思考。但当你熟练掌握向量化操作后,你会发现,这里面有固定的设计模式(对应少量的向量化技巧),可以灵活运用到很多不同的代码片段中。
中英文对照
- 逻辑回归 Logistic Regression
- 批量梯度上升法 batch gradient ascent
- 截距 intercept term
- 对数似然函数 the log likelihood
- 导函数 derivative
- 梯度 gradient
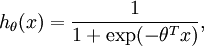
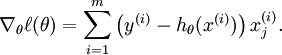
最短路径)

条件最短路径)
)
线性规划问题)

最小生成树)
关键路径法)




探讨)


)



