目录
1.线性预测函数
2.预测方差最小原则
3.线性最小方差预测的性质
AR(p)序列的预测
例题
R语言预测举例
MA(q)序列的预测
例题
ARMA(p,q)序列预测
例题
小结
序列只有为非白噪声时才可以进行预测哦!!
1.线性预测函数
根据平稳性和可逆性,ARMA(p,q)模型可写成
传递形式:
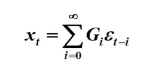
逆转形式:
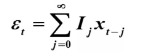
则可以写成:
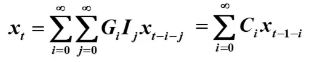
由此可得预测函数
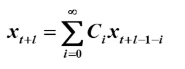
则 步预测函数为:
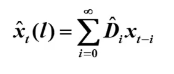
2.预测方差最小原则
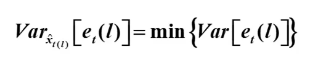
如何达到最小?
传递形式:
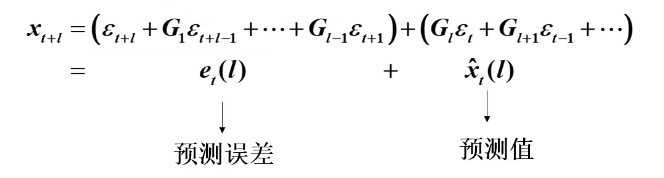
写成已知值的形式:预测误差此时为0

预测误差:
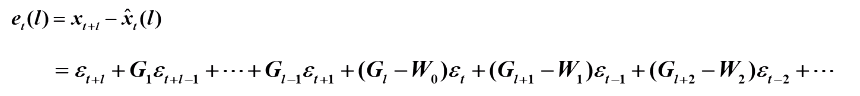
预测误差的方差
![]()
达到最小时:
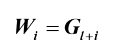
3.线性最小方差预测的性质
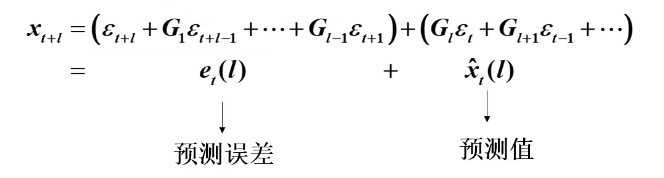
条件无偏最小方差估计值:
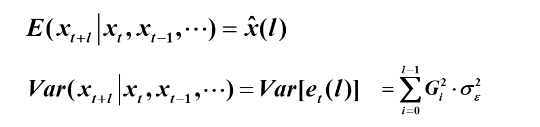
正态假设下置信区间
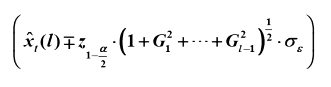
AR(p)序列的预测
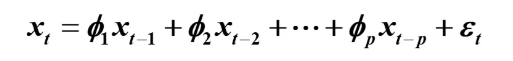
预测值:
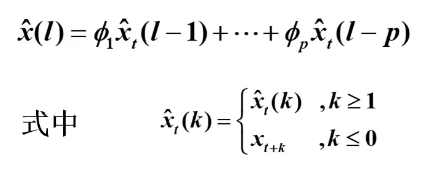
预测方差:
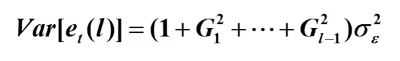
95%的置信区间:
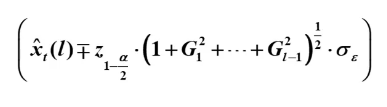
例题
例:已知某超市月销售额近似服从AR(2)模型(单位:万元/每月)
![]()
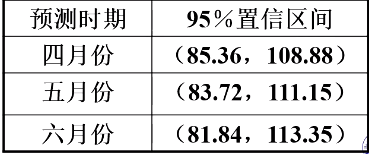
某年第一季度月销售额(万元)分别为:101,96,97.2;请确定该超市第二季度每月销售额的95%的置信区间
(1) 预测值计算
四月份:
![]()
五月份:
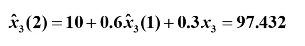
六月份:
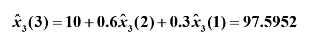
(2) 预测方差计算
方差公式:
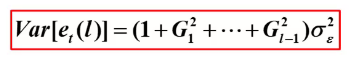
Green函数:
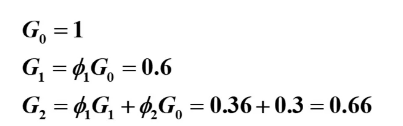
则计算的方差为:
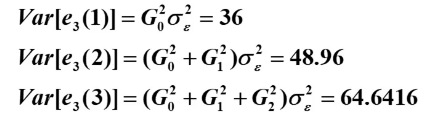
(3) 置信区间
公式:
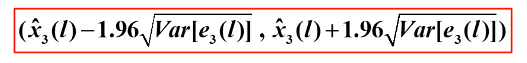
Green函数:
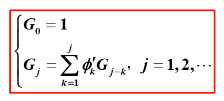
则求得:
R语言预测举例
程序包:forecast

例4-1(续)根据1900—1998年全球7级以上地震发生次数的观察值,预测1999-2008年全球7级以上地震发生次数
a<-read.table("D:/桌面/4_1.csv",sep=",",header=T)
x<-ts(a$number,start=1900)
plot(x) #时序图
library(aTSA) #aTSA导入程序包
adf.test(x) #单位根检验
for(i in 1:2)print(Box.test(x,lag=6*i))
acf(x)
pacf(x)
#参数估计
fit1=arima(x,order=c(1,0,0),method="ML")
fit1
#模型显著性检验
ts.diag(fit1)#参数显著性检验
t<-abs(fit1$coef)/sqrt(diag(fit1$var.coef))
t
pt(t,length(x)-length(fit1$coef),lower.tail=F)#预测
library(forecast)
fore1<-forecast(fit1,h=10)
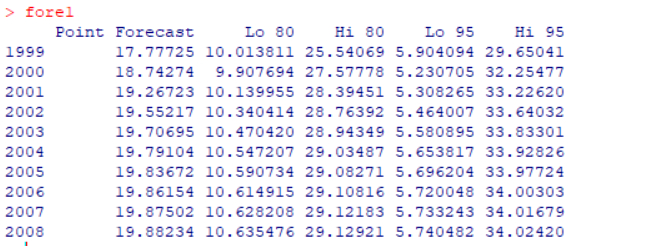
fore1
plot(fore1)
大部分前面都介绍了,我们就只看一下,预测结果吧:

MA(q)序列的预测
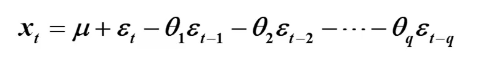
预测值:
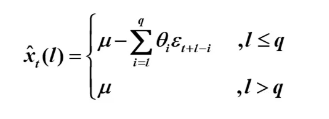
预测方差:
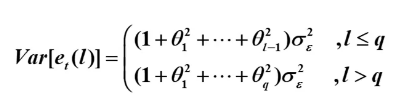
例题
例:已知某地区每年常驻人口数量近似服从MA(3)模型(单位:万人):
![]()
最近3年的常驻人口数量及一步预测数量如下:
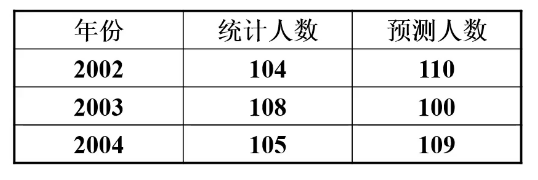
预测未来5年该地区常住人口的95%置信区间
(1) 已知历史随机扰动项计算
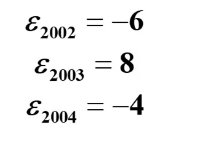
(2) 预测值计算
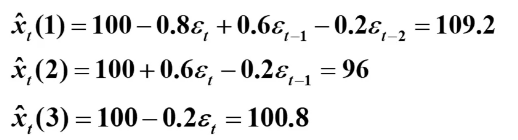
(3)预测方差的计算
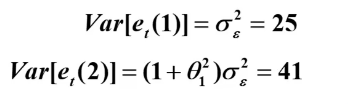
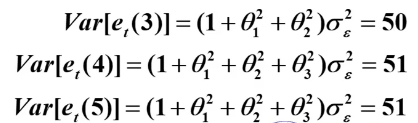
(4) 95%置信区间计算
置信区间公式:
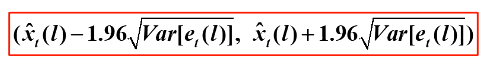
则计算结果为:

ARMA(p,q)序列预测
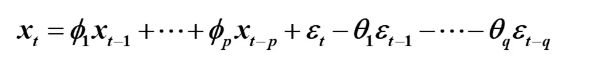
预测值
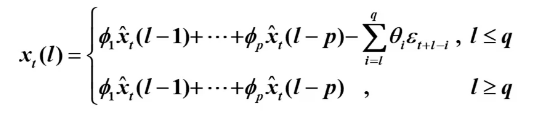
其中
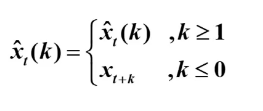
预测方差
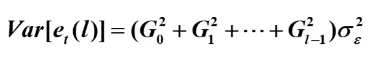
例题
例:已知ARMA(1,1)模型为:
![]()
且x100=0.3 , 100=0.01 。预测未来3期序列值的95%的置信区间。
(1) 计算预测值
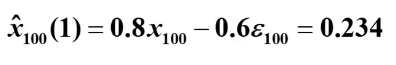
(2)预测方差计算

(3)95%置信区间计算
![]()
则计算结果为:
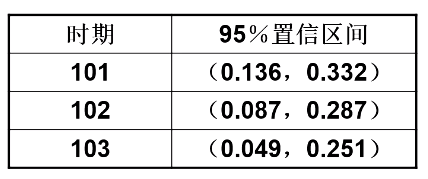
小结
1、线性预测
用现有序列观察值的线性函数可以预测未来任意时刻的序列值2、预测方差最小原则
3、预测方法
预测值按拟合的模型预测,已知数据直接代入,未知序列值用预测植代替,未知扰动忽略
预测方差:
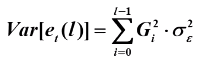
置信区间:
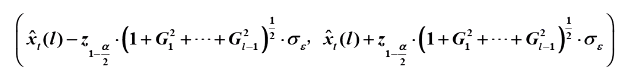

 dtype()



API)

)











