目录
1.疏系数模型的定义
2.拟合ARIMA疏系数模型函数
例题：
小结
1.疏系数模型的定义
ARIMA(p,d,q)模型是指d阶差分后自相关最高阶数为p，移动平均最高阶数为q的模型，通常它包含p+q个独立的未知系数:
如果该模型中部分自相关系数 ,1≤j<p或部分移动平滑系数
,1≤k <q为零，即原模型中有部分系数省缺了，那么该模型称为疏系数模型。
ARIMA((1,4),1,1)表示差分部分1阶，自回归部分1、4参数非零，2、3参数为0，移动平均部分1阶。
2.拟合ARIMA疏系数模型函数
例题：
例5.8 对1917年一1975年美国23岁妇女每万人生育率序列建模
相关代码如下：
#读取数据
a<-read.table('D:/桌面/5_8.csv',sep=',',header=T)
a #输出上面读取的数据内容y<-ts(a$fertility,start=1917) #建立时序plot(y) #绘制时序图adf.test(y) #对时序y进行平稳性检验
dify = diff(y) #求时序y的差分
library(aTSA) #载入程辑包：‘aTSA’
adf.test(dify) #对差分进行平稳性检验#白噪声检验
for(i in 1:2)print(Box.test(dify,lag=6*i,type='Ljung-Box')) #LB检验#定阶
acf(dify) #自相关图
pacf(dify) #偏自相关图返回：
在这里，就不对读取数据，时序图，平稳性检验，白噪声检验结果进行讲解了，有疑问的可以留言或者看之前的博客内容，接下来，主要对定阶进行讲解，也就是自相关图和偏自相关图结果进行讲解。
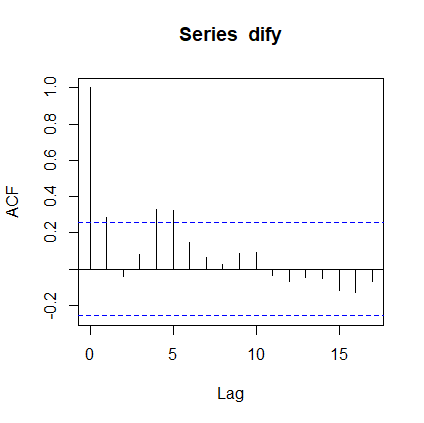
由图可知，它可以是5阶截尾也可以是拖尾，至于如何具体定义，实在说不准，可以看看模型的拟合结果，进行比较后再进一步确定。
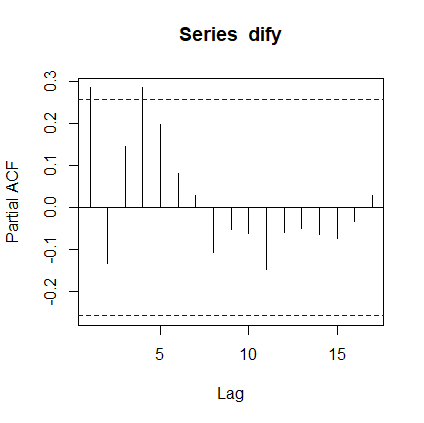
由图可知，可以看成4阶截尾，也可以说是拖尾。
根据不同的类型可以分成如下：
结果分析：
- 如果把差分的自相关系数看成拖尾，偏自相关系数看成截尾，我们可以建立 AR(4)模型；
- 则原序列可以看成ARIMA(4,1,0)模型。
- 如果把差分的自相关系数看成截尾，偏自相关系数看成拖尾，我们可以建立 MA(5)模型；
- 则原序列可以看成ARIMA(0,1,5)模型。
- 如果把差分的自相关系数看成拖尾，偏自相关系数也看成拖尾，我们可以建立 ARMA(1,1)模型或ARMA(1,4)模型或ARMA(5,4)模型；如果看成ARMA(1,1)模型，则原序列可以看成ARIMA(1,1,1)模型。
在这里我们以 ARIMA(4,1,0) 为例进行拟合，又因为偏自相关图的1阶和4阶有值，2阶和3阶为0，所以还可以进一步写出 ARIMA((1,4),1,0) : 用式子可以表示为
#拟合模型，白噪声无法建立模型
yfit1<-arima(y,order=c(4,1,0),transform.pars=F,fixed=c(NA,0,0,NA))
yfit1返回;
则可得解析式为：
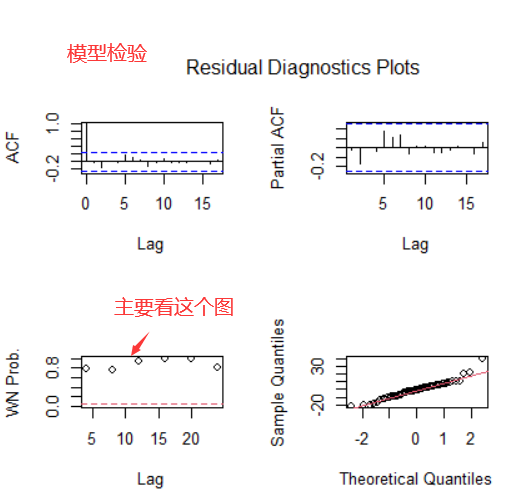
对上述模型进行检验如下：
#模型检验 主要看第三个图
ts.diag(yfit1)
#参数检验
t<-abs(yfit1$coef)/sqrt(diag(yfit1$var.coef))
pt(t,length(y)-length(yfit1$coef),lower.tail=F)返回：
最后对模型进行预测：
library(forecast) #载入程辑包：‘forecast’
yfore<-forecast(yfit1,h=5) #预测5年的
yfore #输出预测结果
plot(yfore) #时序图返回：
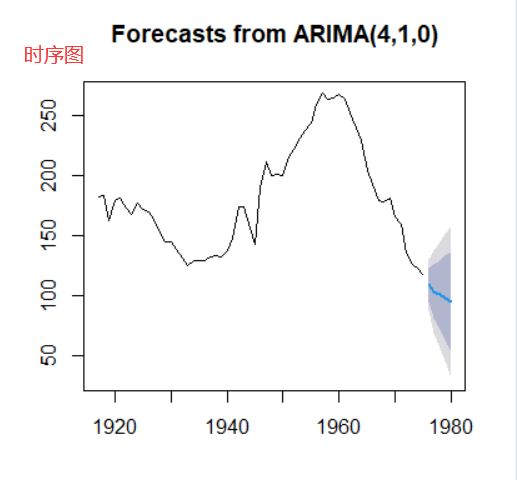
阴影部分是百分之80，和百分之95的置信区间。
小结
- 疏系数模型
- ARIMA(p.d,q)模型中部分系数为0，省缺了。
- arima(x.order=,include.mean=,method=transform.pars=,fixed=)
