目录
ARIMA乘法季节模型
例题1
例题 2
例题3
ARIMA乘法季节模型
序列的季节效应、长期趋势效应和随机波动之间有着复杂的相互关联性,简单的季节模型不能充分地提取其中的相关关系，这时常采用乘积季节模型。
例题1
我国1949-2008年年末人口总数（单位：万人）。选择适当的指数平滑法拟合该序列的长期趋势，并作5期预测。
代码：
加载数据：
a<-read.table('D:/桌面/大三下作业/时间序列/实验报告6/习题4-5.csv',sep=',',header=T) #读取数据
x<-ts(a$population,start=1949)
plot(x,main='时序图') #绘制时序图返回：
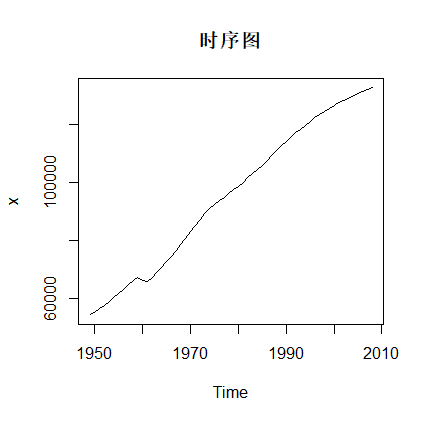
由时序图可知，该序列为显著的线性递增序列，可以使用holt两参数指数平滑法进行趋势拟合和预测，或使用ARIMA ( 1,1,0）模型进行拟合和预测。
拟合模型：
fit1<-HoltWinters(x,gamma=F) #进行2参数指数平滑法进行拟合
fit1 #输出拟合结果返回：
plot(fit1,main='拟合结果时序图') #对拟合结果绘制时序图返回：
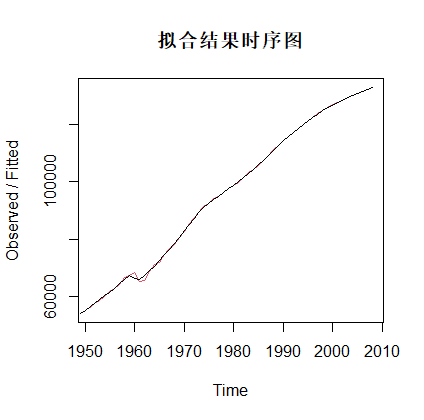
由于没有指定平滑系数的值，所以R基于最优拟合原则计算出平滑系数：
通过Holt两参数指数平滑法，不断迭代，得到最后一期的参数估计值为：
则未来任意k期的预测值为：
进行5期预测：
fore1<-forecast(fit1,h=5)
fore1返回：
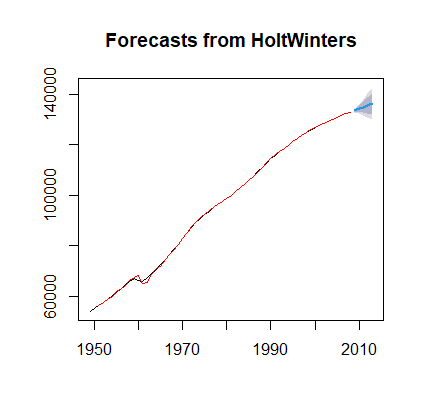
plot(fore1) #对预测结果绘制时序图
lines(fore1$fitted,col='red') #拟合值
返回：
例题 2
某地区1962-1970年平均每头奶牛的月度产奶量数据（单位：磅）。
（1）绘制该序列的时序图，直观考查该序列的特点（有无趋势和季节）。
（2）选择适当的指数平滑法预测下一年该地区奶牛的月度产奶量。写出指数平滑模型、预测模型，预测值和80%、95%的置信区间，绘制预测图。
(1)
加载数据：
a<-read.table('D:/桌面/大三下作业/时间序列/实验报告6/习题4-7.csv',sep=',',header=T)
x<-ts(a$ milk_yield,start=c(1962,1),frequency=12)
绘制时序图：
plot(x,main='时序图') #绘制时序图返回：
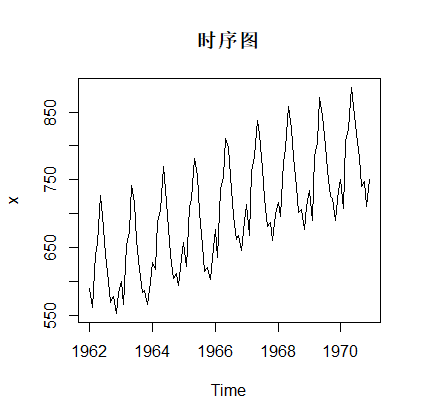
从时序图中可以看到，该序列具有明显的线性递增趋势以及以年为周期的季节效应, 所以可以确定这个序列受到2个因素的影响：长期趋势、季节效应，由于季节性没有随趋势变化而发生显著变化，所以可选择加分模型。
（2）
指数平滑模型预测：
拟合：
| xfit1<-HoltWinters(x) #三参数指数平滑模型拟合 xfit1 |
返回：
由于没有特别指定平滑系数的值，所以R基于最优拟合原则计算出平滑系数：
通过Holt-winters三参数指数平滑加法迭代公式，得到三参数的最后迭代值为：
参数的最后12个估计值对应的是12个月的季节指数，见表1.
表1
| 月份j | 季节指数 | 月份j | 季节指数 |
| 1 | -14.0658 | 7 | 33.47357 |
| 2 | -53.0368 | 8 | -11.9391 |
| 3 | 37.0976 | 9 | -54.9495 |
| 4 | 50.88901 | 10 | -50.0478 |
| 5 | 109.6942 | 11 | -77.2317 |
| 6 | 82.63421 | 12 | -35.5463 |
下一年该地区奶牛的月度产奶量的预测模型为：
进行预测：
| library(forecast) fore1<-forecast(xfit1,h=12) fore1 |
返回：
| plot(fore1) #绘制时序图 lines(fore1$fitted,col=2) #绘制拟合趋势 |
返回：
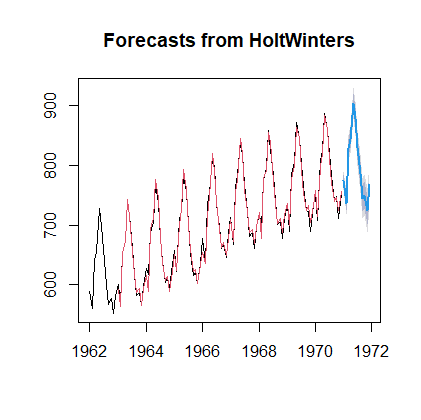
用以前知识实现模型预测：
差分运算：
| dif1<-diff(diff(x),12) #1阶差分12步 plot(dif1) #绘制1阶差分的时序图 |
返回：
平稳性检验：
| library(aTSA) adf.test(dif1) |
返回：
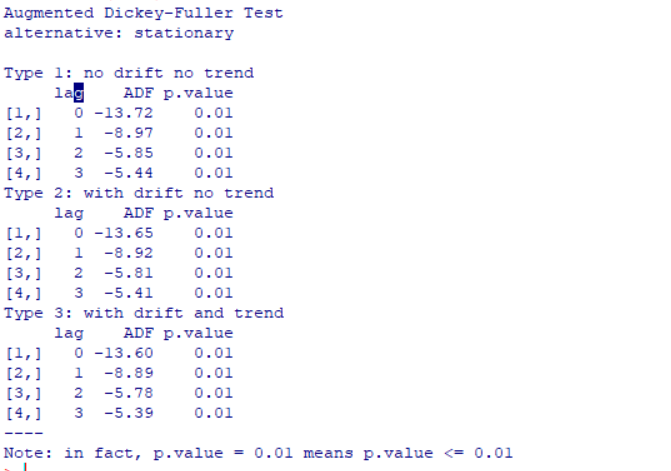
由结果可知，三期结果的p值均小于0.05，所以认为该序列平稳
白噪声检验：
| for(i in 1:2)print(Box.test(dif1,lag=6*i)) |
返回：
由结果可知，6期和12期的p值均小于0.05，所以拒绝原假设，认为不是白噪声序列
模型定阶：
| acf(dif1,main='自相关系数图') pacf(dif1,main='偏自相关系数图') |
返回：
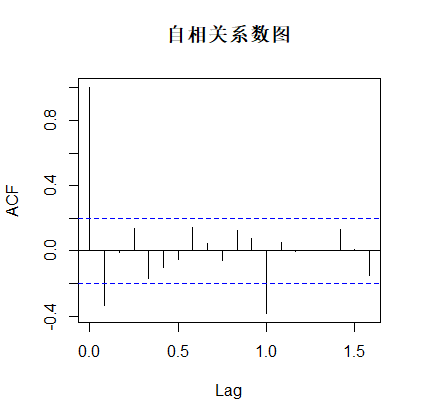
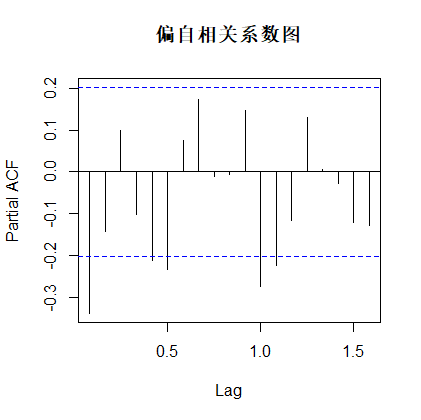
由自相关系数图可知，可以认为自相关系数1阶拖尾，由偏自相关系数图可知，可以认为偏自相关系数1阶拖尾，则可以建立定阶为ARIMA(1,1,0)
拟合模型：
| fit2<-arima(x,order=c(1,1,0),seasonal=list(order=c(0,1,1),period=12)) fit2 |
返回：
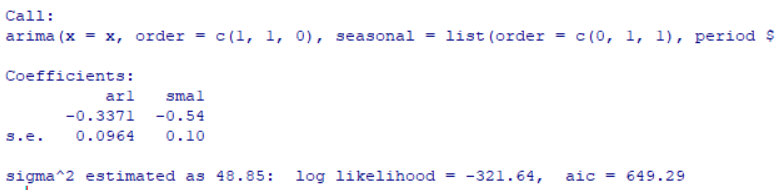
对模型进行检验：
| library(aTSA) ts.diag(fit2) |
返回：
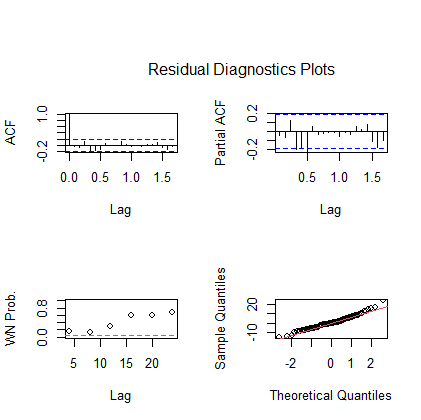
由图可知拟合效果良好。
进行预测：
| fore2<-forecast(fit2,h=12) fore2 |
返回：
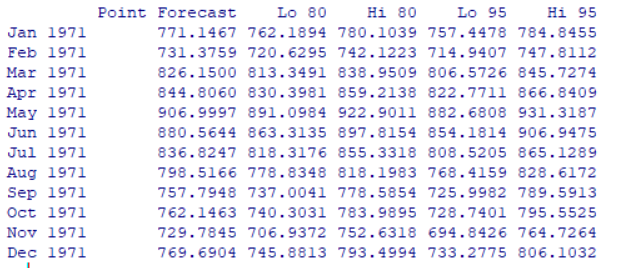
绘制时序图：
| plot(fore2) lines(fore2$fitted,col=2) |
返回：
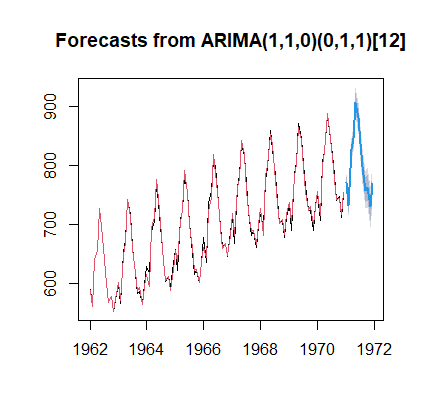
例题3
2013-2020年中国农村居民人均消费支出累计值(元)如附件所示。
（1）绘制该序列的时序图，直观考查该序列的特点（有无趋势和季节）。
（2）选择适当的指数平滑法预测未来3年中国农村居民人均消费支出累计值(元)。写出指数平滑模型、预测模型，预测值和80%、95%的置信区间，绘制预测图。
（1）
加载数据：
| a<-read.table('D:/桌面/大三下作业/时间序列/实验报告6/农村居民人均消费支出累计值(元).csv',sep=',',header=T) x<-ts(a$zhichu,start=c(2013,1),frequency=4) |
| plot(x,main='时序图') #绘制时序图 |
返回：
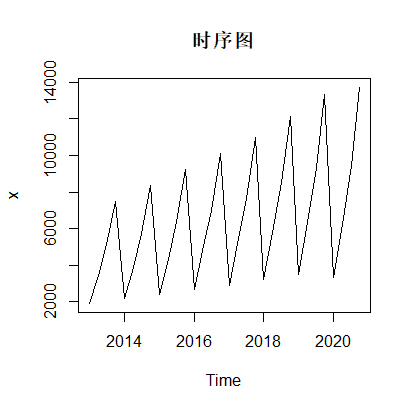
从时序图中可以看到，该序列具有明显的线性递增趋势以及以年为周期的
季节效应, 所以可以确定这个序列受到2个因素的影响：长期趋势、季节效应，由于季节性有随趋势变化而发生显著变化，所以可选择乘法模型。
（2）
指数平滑模型预测：
拟合：
| xfit1<-HoltWinters(x,seasonal="mult") #三参数指数平滑模型拟合 xfit1 |
返回：
由于没有特别指定平滑系数的值，所以R基于最优拟合原则计算出平滑系数：
通过Holt-winters三参数指数平滑乘法迭代公式，得到三参数的最后迭代值为：
参数的最后4个估计值对应的是4个季度的季节指数，见表2.
表2
| 季度 | 1季度 | 2季度 | 3季度 | 4季度 |
| 0.45802 | 0.786094 | 1.135653 | 1.620233 |
该序列向前任意K期的预测值等于
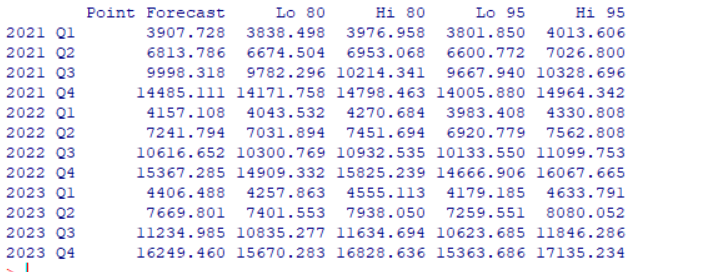
对为来3年进行预测：
| library(forecast) fore1<-forecast(xfit1,h=12) fore1 |
返回：
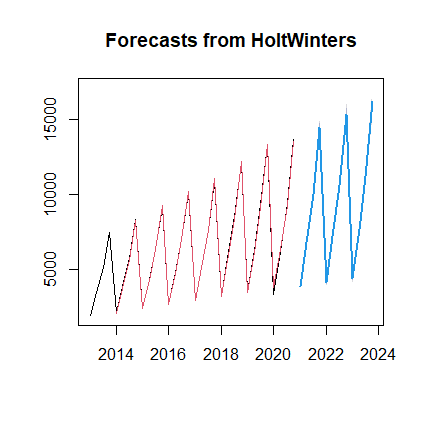
| plot(fore1) #绘制时序图 lines(fore1$fitted,col=2) #绘制拟合趋势 |
返回：
