目录

ARIMA加法季节模型

ARIMA加法季节模型函数

例题

---

ARIMA加法季节模型

季节效应和其它效应之间是加法关系

通过简单的趋势差分、季节差分之后转化为平稳，模型结构通常如下

ARIMA加法季节模型函数

例题

部分数据：

time	x
Jan-93	977.5
Feb-93	892.5
Mar-93	942.3
Apr-93	941.3
May-93	962.2
Jun-93	1005.7
Jul-93	963.8
Aug-93	959.8
Sep-93	1023.3
Oct-93	1051.1
Nov-93	1102

数据链接：蓝奏云

R程序如下：

读取数据：

a<-read.table('D:/桌面/6_2.csv',sep=',',header=T) #读取数据
x<-ts(a$unemployment_rate,start=c(1962,1),frequency=4)# 时序图
plot(x,main='时序图')

返回时序图：

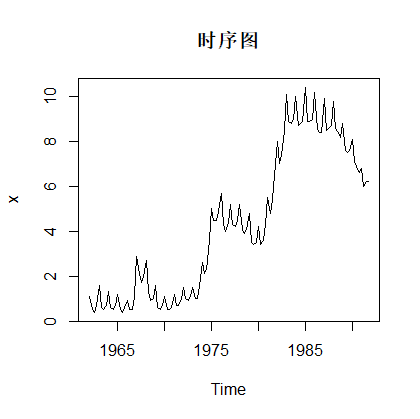
差分处理：

# 1阶4步差分
xdif<-diff(diff(x),4)#时序图
plot(xdif,main='差分后时序图')

返回：

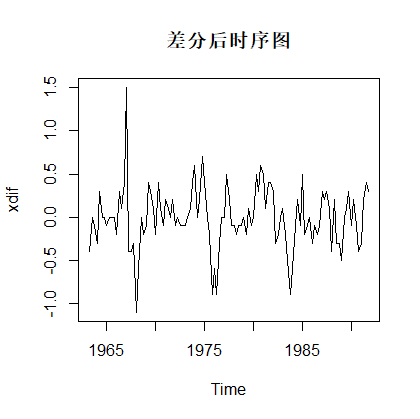
单位根检验：

# 导入库
library(aTSA)
# 差分后单位根检验
adf.test(xdif) 

返回：

由结果可知，p值均小于0.05，所以通过了检验。

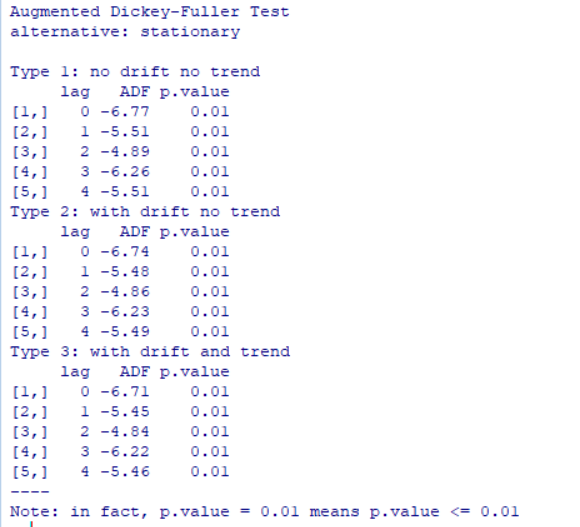
差分后白噪声检验：

for(i in 1:2)print(Box.test(xdif,lag=6*i))

返回：

由结果知，6期、12期的序列结果的p值均小于0.05，所以该序列通过了白噪声检验。

差分后自相关和偏自相关图：

acf(xdif,main='自相关图')
pacf(xdif,main='偏自相关图')

返回：

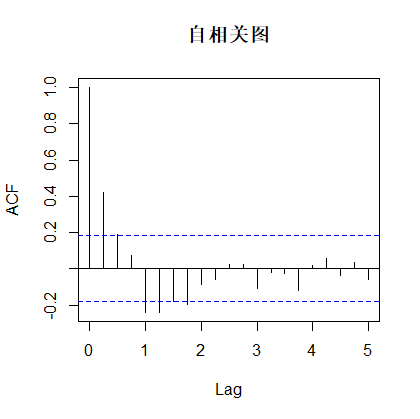
由自相关图知，该序列具有拖尾性。

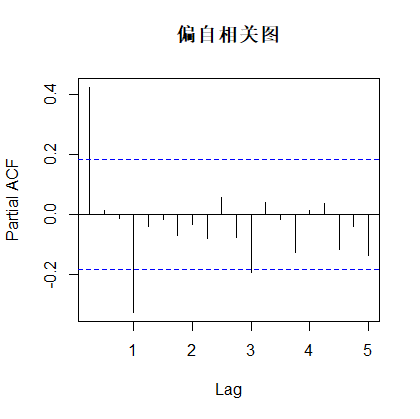
由偏自相关图知，该序列具有4阶截尾性。

综上，差分后该序列可建立，AR(4)，又因为原序列经过了1阶4步差分，所以原序列的拟合模型可以为疏系数模型，定阶为ARIMA((1,4),(1,4),0))

疏系数模型：

#需人工干预
xfit<-arima(x,order=c(4,1,0),transform=F,fixed=c(NA,0,0,NA),seasonal=list(order=c(0,1,0),period=4)) 

返回：

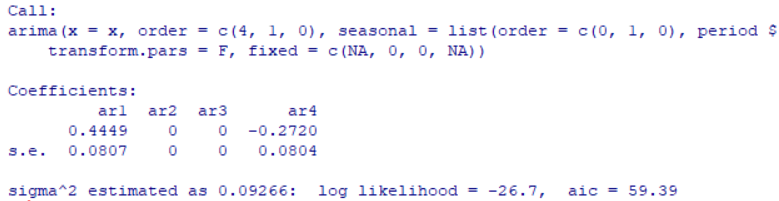
 所以可得模型为：

                               其中

模型检验：

ts.diag(xfit)

返回：

由结果可知，该模型拟合效果很好。

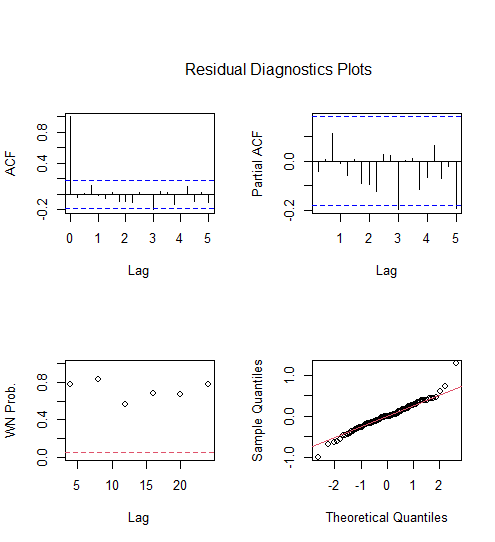
三年预测：

# 导入库
library(forecast)
# 预测
xfore<-forecast(xfit,h=12)

 返回：

# 绘制时序图
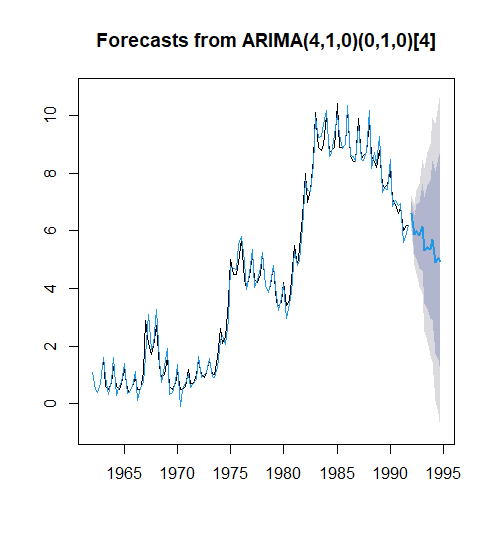
plot(xfore)
lines(xfore$fitted,col=4)

返回：

由预测时序图结果可知，该模型的拟合效果较好。