多元时间序列分析 —— 因果检验

因果检验

因果关系的识别

例

Granger 因果关系定义

两变量之间的4种因果关系

Granger因果检验

1.假设条件

2.检验统计量

例

进行Granger因果检验应该注意的问题

因果检验

因果关系的识别

对于多元时间序列而言，如果能找到对响应变量有显.著影响的输入序列，并且能验证它们之间具有协整关系，这对准确预测响应变量的波动，或者通过控制输入序列的取值，间接控制响应变量的发展都是非常有用的。但前提是输入序列和响应序列之间具有真正的因果关系，而且一定是输入序列为因，响应序列为果。
这种因果关系的认定，在某些情况下是清晰明确的。比如T例7-3，对于中国农村家庭而言，一定是量入为出，收入的多少影响了支出的多少，所以一定是收入为因，支出为果。这个例子中输入变量和因变量很好识别。
但是在有些领域，变量之间的关系可能比较复杂，因果关系的识别并不是一自了然的。无其是在经济、金融领域，多个变量都来自相同领域，甚至是同一个系统，彼此之间多半有相关关系，但彼此之间电l天果关系却并不明确。
我们在建立协整模型时，需要先确定变量之间的因界关系

例

1983年D.A. N icols想研究对白领阶层薪水调整有决定性影响的宏观经济因素。他收集了四个相关变量:
( 1 )白领阶层的平均年薪y:
( 2 )当年的通货膨胀率CPI:(3）当年的失业率U;
( 4）当年的最低工资标准MW。
·他想研究的响应变量是白领阶层的平均年薪w，那么剩下的三个变量是不是导致年新变化的因变量呢?
如果单纯从逻辑上分析，上述四个变量之间的因果关系，我们很难直接识别。

因为既有可能是通货膨胀率上涨，导致雇主不得不给白领雇员涨薪，这时确实是 CPI 为因， w 为果，也有可能是雇主先给白领阶层涨了薪水，导致商品或服务价格上涨，维而推高了通货膨胀率，这时 W 为因， cPI 为果．因果关系不同，回归模型自变量和因变量的位置就不同，因此 CPI 能不能作为年薪 W 的输人变量并不明确。
失业率 U 与年薪 W 的关系也是如此．既有可能是失业率高导致白领被迫降低年薪以保全工作岗位，也有可能是雇员工资太高，雇主为降低成本增加裁员，导致失业率上升．这两种情况下，因果关系正好是反的．
最低工资标准 MW 与年薪 W 的关系也有多种可能．既有可能是最低工资标准提高，推高了平均年薪，也有可能是平均年薪增加，推高了最低工资标准，甚至还有第三种可能，就是它们尽管都是薪资水平，但领取的人群不同，有可能它们彼此之间相互独立，且没有什么相互影响，那就连回归模型都不必建了
在经济、金融领域，这种多个变量都来自相同领域，甚至是同一个系统，但彼此之间的因果关系并不明确的现象比比皆是，那么在协整建模时，首先需要检验变量之间
的因果关系。
Granger 在1969年给出了序列因果关系的定义， T . J . Surgent 在1976年根据 Granger 对因果性的定义，给出了因果关系检验方法，这使得判断多个序列之间的因
果关系有了明确的定义和统计检测方法 .

Granger 因果关系定义

因果关系，一定是原因导致了结果。所以从时间上说，应该是原因发生在前，结果产生在后。就影响效果而言，×事件发生在前，而且对Y事件的发展结果有影响，X事件才能称为Y事件的因。基于对这种因果关系的理解，1969年Granger给出了序列间因果关系的定义，我们称之为Granger因果关系定义。

Granger因果关系定义:假设X和Y是宽平稳序列，

(1) $I_t$ 为 t 时刻所有有用信息的集合

$I_t=\left \{ x_t,x_{t-1},\cdots ,y_t,y_{t-1},y_{t-2},\cdots \right \}$

(2) $X_t$ 为 t 时刻所有x序列信息的集合

$X_t=\left \{ x_t,x_{t-1},x_{t-2},\cdots \right \}$

(3) $\sigma^2(\cdot )$ 为方差函数

序列x是序列y的Granger原因，当且仅当 y 的最优线性预测函数使得下式成立:

$\sigma^2(y_{t+1}|I_t)< \sigma^2(y_{t+1}|I_t-X_t)$

式中， $\sigma^2(y_{t+1}|I_t)$ 是使用所有可获得的历史信息（其中也包含x序列的历史信息〉得到的y序列一期预测值的方差： $\sigma^2(y_{t+1}|I_t-X_t)$ 是从所有信息中刻意扣除r序列的历史信息得到的y序列一期预测值的方差。
如果 $\sigma^2(y_{t+1}|I_t)< \sigma^2(y_{t+1}|I_t-X_t)$ ，则说明r序列历史信息的加入能提高y序列的预测精度。进而反推出序列x是因，序列y是果，简记为x一>y。

两变量之间的4种因果关系

·根据Granger因果关系定义，在两个序列之间存在4种不同的因果关系(不考虑两变量之间当期影响)

(1) x和y相互独立，简记为（x,y);
(2) x是y的Granger 原因，简记为(x->y);
(3) y是x的Granger 原因，简记为(x<-y);
(4)x和y互为因果，这种情况称为x和y之间存在反馈（feedback）关系，简记为
(x<->y)。

Granger因果检验

1.假设条件

Granger因果检验认为绝大多数时间序列的生成过程是相互独立的，所以原假设是序列x不是序列y的Granger原因，备择假设是序列x是序列y的Granger原因。
构造序列y的最优线性预测函数，不妨记作:

$y_t=\beta _0+\sum_{k=1}^{p}\beta_ky_{t-k}+\sum_{k=1}^{q}\alpha_kx_{t-k}+\sum_{k=1}^{l}\gamma_kz_{t-k}+\varepsilon_t$

此时，Granger因果检验的假设条件可以等价表达为

$H_0:\alpha_1=\alpha_2=\cdots =\alpha_q=0\leftrightarrow H_1:\alpha_1,\alpha_2,\cdots ,\alpha_q$ 不全为0

2.检验统计量

检验统计量:有多种方法构建Granger因果检验的统计量，在此介绍F检验统计量的构造原理。在该检验方法下，需要拟合两个回归模型
在原假设成立的情况下，拟合序列y的有约束预测模型

在备择假设成立的情况下，拟合序列y的无约束预测模型

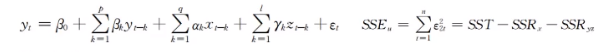
检验统计量

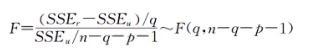
例

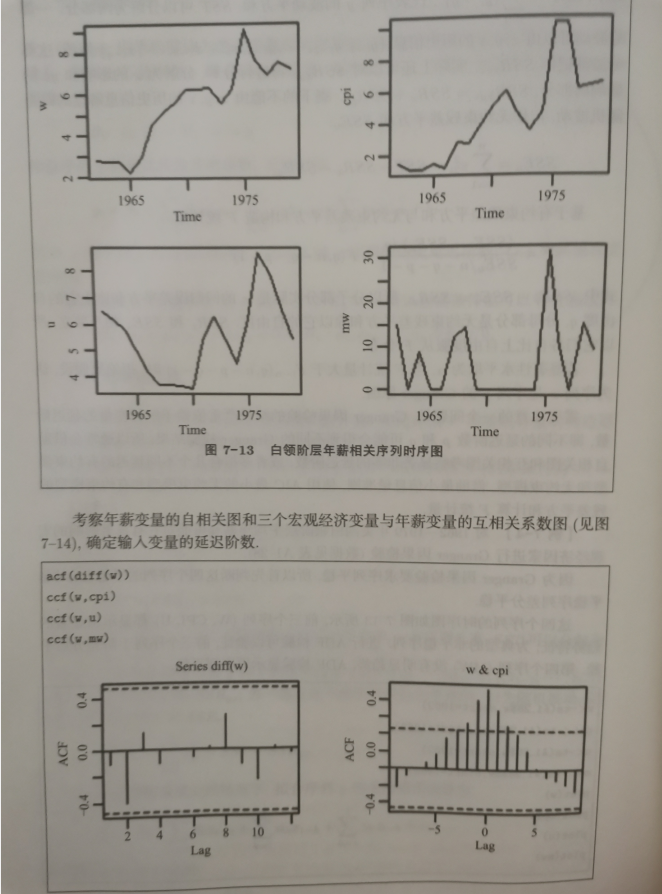
对1962-1979年美国白领阶层平均年薪和可能对它有显著影响的宏观经济因素进行Granger因果检验。
第一步:检验序列平稳性
- 前三个序列(W, CP1,U) 1阶差分后平稳·
- 第四个序列(MW)原序列平稳

懒了，直接贴书了，哈哈哈

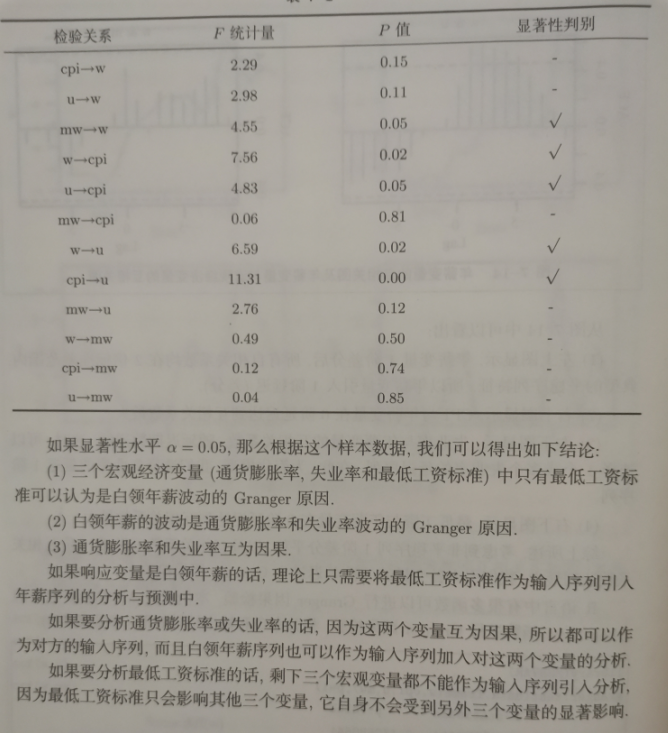
进行Granger因果检验应该注意的问题

检验结果只说明样本数据特征。例7-4的Granger因果检验得出结论:白领年薪的波动受最低工.资的影响，但不受通货膨胀率和失业率的显著影响。这个因果结论是基于这批样本数据得出的。如果换一批数据，或增加样本数据量，得出的因渠判嗟可能会完全不一样。这也就是说，Granger因果检验的结果会受到样本随机性的影响。样本容量越小，样本随机性的影响就越天。所以最好在样本容量比较大时进行Granger因果检验，以保证检验结果相对稳健。
Granger因果检验即使显著拒绝原假设，也不能说明两个序列间具有真正的因果关系。Granger因果检验的构造思想是:使响应变量预测精度有显著提高的自变量可以视作响应变量的因。这里面存在一个逻辑漏洞:如果变量x是变ry的因，那么知道x的信息对预测y是有帮助的，这个结论是对的。但反过来认为，有助于预测精度提高的变量都是响应变量的因，就不一定正确了。这就意味着，在进行Granger因果检验时，即使得出因果关系显著成立的结论，也仅仅是预测精度提高的统计显著性判断，并不煮味若两个变量之间一定存在真正的因果关系。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/564729.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！