求一个任意实数c的算术平方根g的算法设计思想

求一个任意实数c的算术平方根g的算法设计思想_算法复习第四篇——贪心法

公元2020年5月5日，距离算法考试仅剩4天。

一、知识归纳

1.设计思想

只根据当前已有的信息就做出选择，而且一旦做出了选择，将来无论如何都不能更改
不从整体最优考虑，所做的选择只是在某种意义上的局部最优
这种选择并不总能获得整体最优解（Optimal Solution），但通常能获得近似最优解（Near-Optimal Solution）

动态规划法通常以自底向上的方式求解各个子问题。
贪心法则通常以自顶向下的方式做出一系列的贪心选择。

2.示例

【找钱问题】假设有面值为5元、2元、1元、5角、2角、1角的货币，需要找给顾客4元6角现金，使付出的货币的数量最少。

【思路】

首先选出1张面值不超过4元6角的最大面值的货币，即2元，再选出1张面值不超过2元6角的最大面值的货币，即2元，再选出1张面值不超过6角的最大面值的货币，即5角，再选出1张面值不超过1角的最大面值的货币，即1角，总共付出4张货币。
在付款问题每一步的贪心选择中，在不超过应付款金额的条件下，只选择面值最大的货币，而不去考虑在后面看来这种选择是否合理，而且它还不会改变决定：一旦选出了一张货币，就永远选定。
贪心选择策略是尽可能使付出的货币最快地满足支付要求，其目的是使付出的货币张数最慢地增加

3.基本要素

(1) 最优量度标准（正确的贪心策略，贪心选择性质）

贪心法求解问题的核心问题
根据该量度标准，实行多步决策进行求解
在该量度意义下，每步的贪心选择是局部最优的
得到全局最优解

(2) 求解的问题有最优子结构性质(最优性原理)

一个问题的最优解包含其子问题的最优解

注：贪心算法的基本要素是贪心选择性质和最优子结构性质。

4.求解过程

(1) 分解

将原问题分解为若干相互独立的阶段；

(2) 求解

对于每个阶段求局部最优解，即根据贪心策略进行贪心选择；
在每个阶段，选择一旦做出就不可更改。

(3) 合并

将各个阶段的解合并为原问题的一个可行解。

5.相关概念

(1) 候选解集合C

问题的可能解
问题的最终解均取自于该候选集合

(2) 解集合S

随着贪心选择的进行不断扩展，直到构成一个满足问题的完整解

(3) 解判定函数solution

检查解集合S是否构成问题的完整解

(4) 选择函数select

贪心策略，这是贪心法的关键
指出哪个候选对象最有希望构成问题的解
通常和目标函数有关

(5) 可行解判定函数feasible

检查解集合中加入一个候选对象是否可行，即解集合扩展后是否满足约束条件

6.贪心法的一般过程

Greedy

二、组合问题中的贪心法

背包问题(物品可切割)
多机调度问题
活动安排问题

1.背包问题

【问题表述】给定n种物品和一个容量为C的背包，物品i的重量是wi，其价值为vi，设xi表示物品i装入背包的情况，背包问题是如何选择装入背包的物品，使得装入背包中物品的总价值最大?

【建立模型】

【贪心策略】

贪心策略一：价值最大优先
因为这可以尽可能快地增加背包的总价值。但是，虽然每一步选择获得了背包价值的极大增长，但背包容量却可能消耗得太快，使得装入背包的物品个数减少，从而不能保证目标函数达到最大。贪心策略二：重量最轻优先
因为这可以装入尽可能多的物品，从而增加背包的总价值。但是，虽然每一步选择使背包的容量消耗的慢了，但背包的价值却没能保证迅速增长，从而不能保证目标函数达到最大。贪心策略三：单位重量价值最大优先
在背包价值增长和背包容量消耗两者之间寻找平衡。

例如，有3个物品，其重量分别是{20, 30, 10}，价值分别为{60, 120, 50}，背包的容量为50，应用三种贪心策略装入背包的物品和获得的价值如图所示。

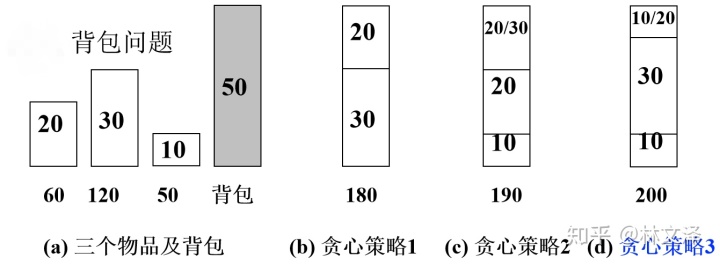
应用第三种贪心策略，每次从物品集合中选择单位重量价值最大的物品，如果其重量小于背包容量，就可以把它装入，并将背包容量减去该物品的重量，然后我们就面临了一个最优子问题——它同样是背包问题，只不过背包容量减少了，物品集合减少了。因此背包问题具有最优子结构性质。

【算法描述】

设背包容量为C，共有n个物品，物品重量存放在数组w[n]中，价值存放在数组v[n]中，问题的解存放在数组x[n]中。

1．改变数组w和v的排列顺序，使其按单位重量价值v[i]/w[i]降序排列；
2．将数组x[1:n]初始化为0；  //初始化解向量
3．i=1;      
4．循环直到(w[i]>C)4.1 x[i]=1;     //将第i个物品放入背包4.2 C=C-w[i];4.3 i++;
5.    x[i]=C/w[i];
void Knapsack(int n,float M,float v[],float w[],float x[])
{Sort(n,v,w);int i;for (i=1;i<=n;i++) x[i]=0;float c=M;for (i=1;i<=n;i++) {if (w[i]>c) break;x[i]=1;c - =w[i];}if (i<=n) x[i]=c/w[i];
}

【算法时间复杂度分析】

该算法的时间主要消耗在将各种物品依其单位重量的价值从大到小排序。因此，其时间复杂性为O(nlog2n)。

注：贪心算法不能解决0/1背包问题，可通过动态规划法解决。

三、图问题中的贪心法

单源最短路径问题 - Dijkstra算法
TSP问题
最小生成树问题 - Prim算法 - Kruskal算法
图着色问题

1.最小代价生成树问题

【问题表述】设G=(V，E)是一个无向连通图，生成树上各边的权值之和称为该生成树的代价，在G的所有生成树中，代价最小的生成树称为最小生成树（Minimal Spanning Trees）。

【贪心策略】

①最近顶点策略任选一个顶点，并以此建立起生成树，每一步的贪心选择是简单地把不在生成树中的最近顶点添加到生成树中。②最短边策略设G = (V,E)是一个无向连通网，令T= (V,TE)是G的最小生成树。从TE={}开始，每一次贪心选择都是在边集E中选取最短边(u,v)，如果边(u, v)加入集合TE中不产生回路，则将边(u,v)加入边集TE中，并将它在集合E中删去。

最近顶点策略—Prim算法

使生成树以一种自然的方式生长
从任意顶点开始，每一步为这棵树添加一个分枝，直到生成树中包含全部顶点

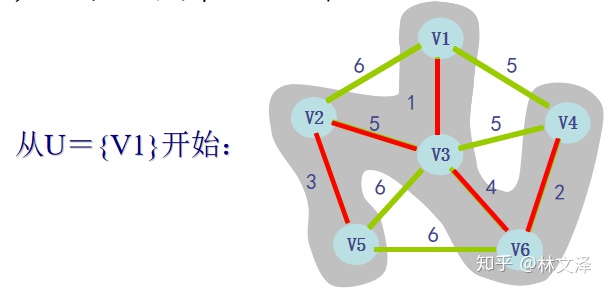
【算法描述】

设图G中顶点的编号为0～n-1

Prim算法1. 初始化两个辅助数组lowcost和adjvex；2. U={u0}; 输出顶点u0;    //将顶点u0加入生成树中3. 重复执行下列操作n-1次3.1 在lowcost中选取最短边，取adjvex中对应的顶点序号k;3.2 输出顶点k和对应的权值；3.3 U=U+{k}；3.4 调整数组lowcost和adjvex；

【算法时间复杂度分析】

设连通网中有n个顶点，则