平衡二叉树(Balancedbinary tree)是由阿德尔森-维尔斯和兰迪斯(Adelson-Velskiiand Landis)于1962年首先提出的,所以又称为AVL树。
定义:平衡二叉树或为空树,或为如下性质的二叉排序树:
(1)左右子树深度之差的绝对值不超过1;
(2)左右子树仍然为平衡二叉树.
平衡二叉树可以避免排序二叉树深度上的极度恶化,使树的高度维持在O(logn)来提高检索效率。
因为插入节点导致整个二叉树失去平衡分成如下的四种情况:

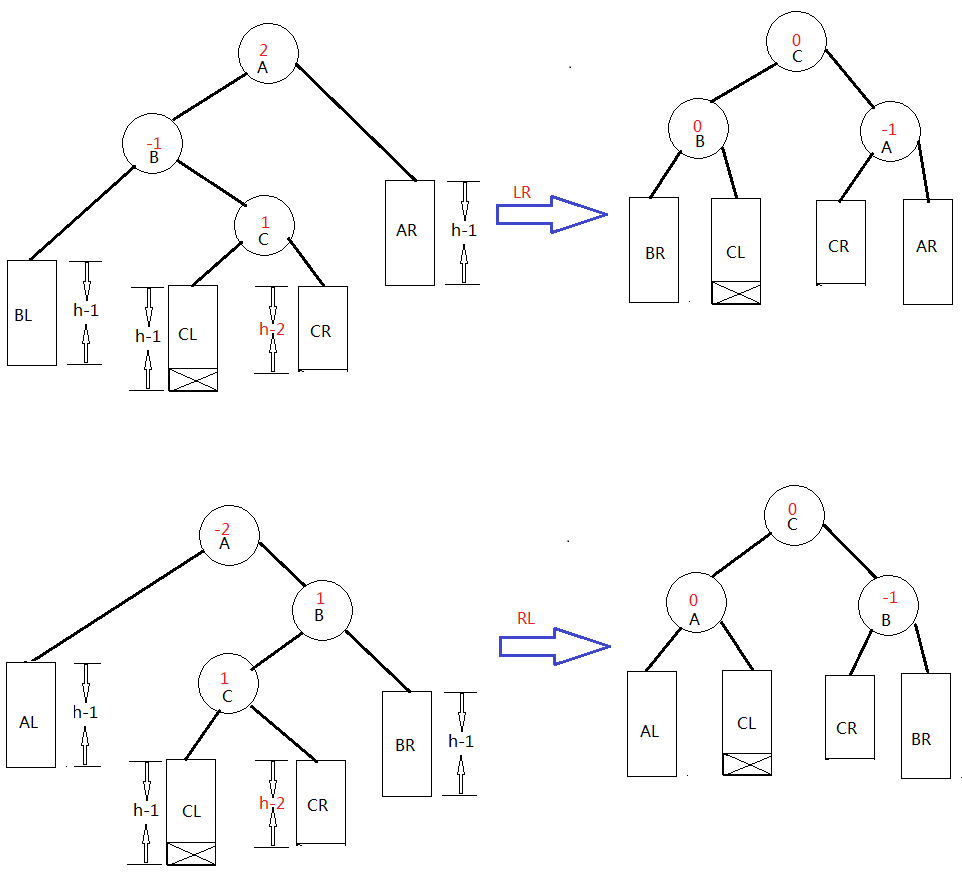
假设由于在二叉排序树上插入节点而失去平衡的最小子数根节点的指针为a(即a是离插入节点最近,且平衡因子绝对值超过1的祖先节点),则失去平衡后进行调整的规律如下:
1.如上图LL单向右旋处理:由于在*a的左子树根节点的左子树上插入节点,*a的平衡因子由1增至2,致使以*a为根节点的子树失去平衡,则需要进行一次向右的顺时针旋转操作。
2.如上图RR单向左旋处理:由于在*a的右子树根节点的右子树上插入节点, *a的平衡因子有-1变为-2,致使以*a为根节点的子树失去平衡,则学要进行一次向左的逆时针旋转操作。
3.如上图LR双向旋转(先左后右)处理:由于在*a的左子树根节点的右子树插入节点,*a的平衡因子有1增至2,致使以*a为根节点的子树失去平衡,则需要进行两次旋转(先左旋后右旋)操作。
4.如上图RL双向旋转(先右后左)处理:由于在*a的右子树根节点的左子树上插入节点,*a的平衡因子由-1变为-2,致使以*a为根节点的子树失去平衡,则需要进行两次旋转(先左旋后右旋)操作。
#include<iostream> #include<cstring> #include<string> #include<queue> #include<map> #include<cstdio> #define LH 1 //左高 #define EH 0 //等高 #define RH -1 //右高 using namespace std;template <typename ElemType> class BSTNode{public:ElemType data;//节点的数据 int bf;//节点的平衡因子BSTNode *child[2];BSTNode(){child[0] = NULL;child[1] = NULL;} };typedef BSTNode<string> BSTnode, *BSTree;template <typename ElemType> class AVL{public:BSTNode<ElemType> *T;void buildT();void outT(BSTNode<ElemType> *T);private:bool insertAVL(BSTNode<ElemType>* &T, ElemType key, bool &taller); void rotateT(BSTNode<ElemType>* &o, int x);//子树的左旋或者右旋void leftBalance(BSTNode<ElemType>* &o);void rightBalance(BSTNode<ElemType>* &o); };template <typename ElemType> void AVL<ElemType>::rotateT(BSTNode<ElemType>* &o, int x){BSTNode<ElemType>* k = o->child[x^1];o->child[x^1] = k->child[x];k->child[x] = o;o = k; }template <typename ElemType> void AVL<ElemType>::outT(BSTNode<ElemType> *T){if(!T) return;cout<<T->data<<" ";outT(T->child[0]);outT(T->child[1]); }template <typename ElemType> void AVL<ElemType>::buildT(){T = NULL;ElemType key;while(cin>>key){if(key==0) break;bool taller = false;insertAVL(T, key, taller);outT(T);cout<<endl;} }template <typename ElemType> bool AVL<ElemType>::insertAVL(BSTNode<ElemType>* &T, ElemType key, bool &taller){if(!T){//插入新的节点,taller=true 那么树的高度增加 T = new BSTNode<ElemType>();T->data = key;T->bf = EH;taller = true;} else {if(T->data == key){taller = false;return false;}if(T->data > key){//向T的左子树进行搜索并插入 if(!insertAVL(T->child[0], key, taller)) return false;if(taller){// switch(T->bf){case LH://此时左子树的高度高,左子树上又插入了一个节点,失衡,需要进行调整 leftBalance(T);taller = false;//调整之后高度平衡 break; case EH:T->bf = LH;taller = true;break; case RH:T->bf = EH;taller = false; break;}}} if(T->data < key) {//向T的右子树进行搜索并插入 if(!insertAVL(T->child[1], key, taller)) return false;switch(T->bf){case LH:T->bf = EH;taller = false; break; case EH:T->bf = RH;taller = true;break; case RH:rightBalance(T); taller = false; break;}}}return true; }template <typename ElemType> void AVL<ElemType>::leftBalance(BSTNode<ElemType>* &T){BSTNode<ElemType>* lchild = T->child[0];switch(lchild->bf){//检查T的左子树的平衡度,并作相应的平衡处理 case LH://新节点 插入到 T的左孩子的左子树上,需要对T节点做单旋(右旋)处理 T->bf = lchild->bf = EH; rotateT(T, 1);break;case RH://新节点 插入到 T的左孩子的右子树上,需要做双旋处理 1.对lchild节点进行左旋,2.对T节点进行右旋 BSTNode<ElemType>* rdchild = lchild->child[1];switch(rdchild->bf){//修改 T 及其左孩子的平衡因子 case LH: T->bf = RH; lchild->bf = EH; break;case EH: T->bf = lchild->bf = EH; break;//发生这种情况只能是 rdchild无孩子节点case RH: T->bf = EH; lchild->bf = LH; break; }rdchild->bf = EH; rotateT(T->child[0], 0);//不要写成 rotateT(lc, 0);//这样的话T->lchild不会改变 rotateT(T, 1);break;} }template <typename ElemType> void AVL<ElemType>::rightBalance(BSTNode<ElemType>* &T){BSTNode<ElemType>* rchild = T->child[1];switch(rchild->bf){//检查T的左子树的平衡度,并作相应的平衡处理 case RH://新节点 插入到 T的右孩子的右子树上,需要对T节点做单旋(左旋)处理 T->bf = rchild->bf = EH; rotateT(T, 0);break;case LH://新节点 插入到 T的右孩子的左子树上,需要做双旋处理 1.对rchild节点进行右旋,2.对T节点进行左旋 BSTNode<ElemType>* ldchild = rchild->child[0];switch(ldchild->bf){//修改 T 及其右孩子的平衡因子 case LH: T->bf = EH; rchild->bf = RH; break;case EH: T->bf = rchild->bf = EH; break;//发生这种情况只能是 ldchild无孩子节点 case RH: T->bf = LH; rchild->bf = EH; break; }ldchild->bf = EH; rotateT(T->child[1], 1);rotateT(T, 0);break;} }int main(){AVL<int> avl;avl.buildT();avl.outT(avl.T);return 0; } /*13 24 37 90 53 0 */
)
C语言之二维数组)

C语言之函数)

C语言之指针)
)
C语言之结构)



)







