平衡二叉树AVL删除

平衡二叉树的插入过程: http://www.cnblogs.com/hujunzheng/p/4665451.html

对于二叉平衡树的删除采用的是二叉排序树删除的思路:

　　假设被删结点是*p，其双亲是*f，不失一般性，设*p是*f的左孩子，下面分三种情况讨论：
　　⑴ 若结点*p是叶子结点，则只需修改其双亲结点*f的指针即可。
　　⑵ 若结点*p只有左子树PL或者只有右子树PR，则只要使PL或PR 成为其双亲结点的左子树即可。
　　⑶ 若结点*p的左、右子树均非空，先找到*p的中序前趋结点*s（注意*s是*p的左子树中的最右下的结点，它的右链域为空），然后有两种做法：
　　　　① 令*p的左子树直接链到*p的双亲结点*f的左链上,而*p的右子树链到*p的中序前趋结点*s的右链上。
　　　　② 以*p的中序前趋结点*s代替*p（即把*s的数据复制到*p中），将*s的左子树链到*s的双亲结点*q的左（或右）链上。

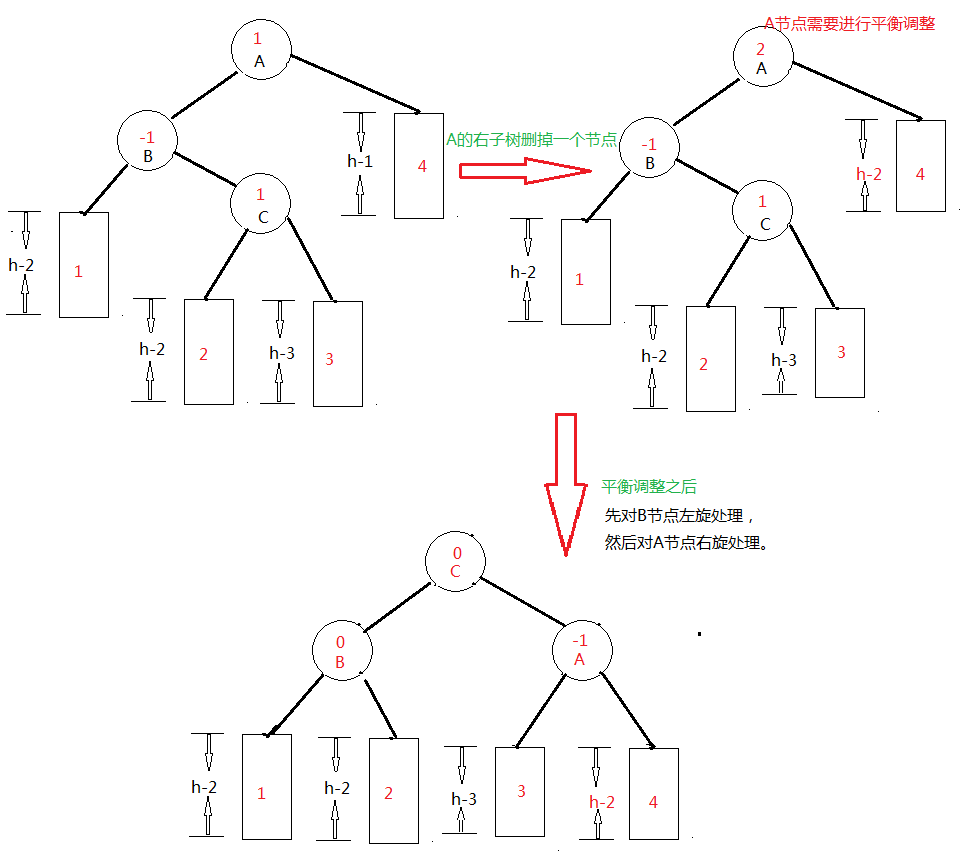
注：leftBalance_del 和 rightBalance_del方法是在删除节点时对左子树和右子树的平衡调整，leftBalance 和 rightBalance方法是在插入节点是对左右子树的平衡调整。 在具体调整的时候，和插入式调整时运用同样的分类方法，这里介绍一种情况，如下图所示（代码部分见代码中的提示）

 

 

#include<iostream>
#include<cstring>
#include<string>
#include<queue>
#include<map>
#include<cstdio>
#define LH 1 //左高 
#define EH 0 //等高 
#define RH -1 //右高 
using namespace std;template <typename ElemType>
class BSTNode{public:ElemType data;//节点的数据 int bf;//节点的平衡因子BSTNode *child[2];BSTNode(){child[0] = NULL;child[1] = NULL;}
};typedef BSTNode<string> BSTnode, *BSTree;template <typename ElemType>
class AVL{public:BSTNode<ElemType> *T;void buildT();void outT(BSTNode<ElemType> *T);void deleteAVL(BSTNode<ElemType>* &T, ElemType key, bool &shorter);bool insertAVL(BSTNode<ElemType>* &T, ElemType key, bool &taller); private:void deleteNode(BSTNode<ElemType>* T, BSTNode<ElemType>* &s, BSTNode<ElemType>* p, bool flag, bool &shorter);void rotateT(BSTNode<ElemType>* &o, int x);//子树的左旋或者右旋void leftBalance(BSTNode<ElemType>* &o);void rightBalance(BSTNode<ElemType>* &o);void leftBalance_del(BSTNode<ElemType>* &o);void rightBalance_del(BSTNode<ElemType>* &o);
};template <typename ElemType>
void AVL<ElemType>::rotateT(BSTNode<ElemType>* &o, int x){BSTNode<ElemType>* k = o->child[x^1];o->child[x^1] = k->child[x];k->child[x] = o;o = k; 
}template <typename ElemType>
void AVL<ElemType>::outT(BSTNode<ElemType> *T){if(!T) return;cout<<T->data<<" ";outT(T->child[0]);outT(T->child[1]);
}template <typename ElemType>
void AVL<ElemType>::buildT(){T = NULL;ElemType key;while(cin>>key){if(key==0) break;bool taller = false;insertAVL(T, key, taller);}
}template <typename ElemType>
void AVL<ElemType>::deleteNode(BSTNode<ElemType>* T, BSTNode<ElemType>* &s, BSTNode<ElemType>* p, bool flag, bool &shorter){if(flag){flag = false;deleteNode(T, s->child[0], s, flag, shorter);if(shorter){switch(s->bf){case LH:s->bf = EH;shorter = false;break; case EH:s->bf = RH;shorter = true;break; case RH:rightBalance_del(s);shorter = false;break;}}} else {if(s->child[1]==NULL){T->data = s->data;BSTNode<ElemType>* ss = s; if(p != T){p->child[1] = s->child[0];} else {p->child[0] = s->child[0];}delete ss;//s是引用类型，不能delete s shorter = true; return ;}deleteNode(T, s->child[1], s, flag, shorter);if(shorter){switch(s->bf){case LH://这是上面配图的情况leftBalance_del(s);shorter = false; break; case EH:s->bf = LH;shorter = true;break; case RH:s->bf = EH;shorter = false;break;}} }
} template <typename ElemType>
bool AVL<ElemType>::insertAVL(BSTNode<ElemType>* &T, ElemType key, bool &taller){if(!T){//插入新的节点，taller=true 那么树的高度增加 T = new BSTNode<ElemType>();T->data = key;T->bf = EH;taller = true;} else {if(T->data == key){taller = false;return false;}if(T->data > key){//向T的左子树进行搜索并插入 if(!insertAVL(T->child[0], key, taller)) return false;if(taller){//
                switch(T->bf){case LH://此时左子树的高度高，左子树上又插入了一个节点，失衡，需要进行调整 
                        leftBalance(T);taller = false;//调整之后高度平衡 break; case EH:T->bf = LH;taller = true;break; case RH:T->bf = EH;taller = false;                        break;}}} if(T->data < key) {//向T的右子树进行搜索并插入 if(!insertAVL(T->child[1], key, taller)) return false;switch(T->bf){case LH:T->bf = EH;taller = false; break; case EH:T->bf = RH;taller = true;break; case RH:rightBalance(T);    taller = false;                    break;}}}return true;
}template <typename ElemType>
void AVL<ElemType>::deleteAVL(BSTNode<ElemType>* &T, ElemType key, bool &shorter){if(T->data == key){BSTNode<ElemType>*q, s; if(!T->child[1]){//右子树为空，然后重接其左子树 q = T;T = T->child[0];shorter = true;//树变矮了 delete q;} else if(!T->child[0]){//左子树为空，重接其右子树 q = T;T = T->child[1];shorter = true;//树变矮了 delete q;} else {//左右子树都非空 ，也就是第三种情况 deleteNode(T, T, NULL, true, shorter);shorter = true;} } else if(T->data > key) {//左子树 deleteAVL(T->child[0], key, shorter);if(shorter){switch(T->bf){case LH:T->bf = EH; shorter = false;break;case RH:rightBalance_del(T);shorter = false;break;case EH:T->bf = RH;shorter = true;break;}}} else if(T->data < key){//右子树 deleteAVL(T->child[1], key, shorter);if(shorter){switch(T->bf){case LH://这是上面配图的情况leftBalance_del(T);shorter = false;
                    break;case RH:T->bf = EH;shorter = false; break;case EH:T->bf = LH;shorter = true;break;}}}
}template <typename ElemType>
void AVL<ElemType>::leftBalance(BSTNode<ElemType>* &T){BSTNode<ElemType>* lchild = T->child[0];switch(lchild->bf){//检查T的左子树的平衡度，并作相应的平衡处理 case LH://新节点 插入到 T的左孩子的左子树上，需要对T节点做单旋(右旋)处理 T->bf = lchild->bf = EH; rotateT(T, 1);break;case RH://新节点 插入到 T的左孩子的右子树上，需要做双旋处理  1.对lchild节点进行左旋，2.对T节点进行右旋 BSTNode<ElemType>* rdchild = lchild->child[1];switch(rdchild->bf){//修改 T 及其左孩子的平衡因子 case LH: T->bf = RH; lchild->bf = EH; break;case EH: T->bf = lchild->bf = EH; break;//发生这种情况只能是 rdchild无孩子节点case RH: T->bf = EH; lchild->bf = LH; break; }rdchild->bf = EH; rotateT(T->child[0], 0);//不要写成 rotateT(lc, 0);//这样的话T->lchild不会改变 rotateT(T, 1);break;}
}template <typename ElemType>
void AVL<ElemType>::rightBalance(BSTNode<ElemType>* &T){BSTNode<ElemType>* rchild = T->child[1];switch(rchild->bf){//检查T的左子树的平衡度，并作相应的平衡处理 case RH://新节点 插入到 T的右孩子的右子树上，需要对T节点做单旋(左旋)处理 T->bf = rchild->bf = EH; rotateT(T, 0);break;case LH://新节点 插入到 T的右孩子的左子树上，需要做双旋处理  1.对rchild节点进行右旋，2.对T节点进行左旋 BSTNode<ElemType>* ldchild = rchild->child[0];switch(ldchild->bf){//修改 T 及其右孩子的平衡因子 case LH: T->bf = EH; rchild->bf = RH; break;case EH: T->bf = rchild->bf = EH; break;//发生这种情况只能是 ldchild无孩子节点 case RH: T->bf = LH; rchild->bf = EH; break; }ldchild->bf = EH; rotateT(T->child[1], 1);rotateT(T, 0);break;}
}template <typename ElemType>
void AVL<ElemType>::leftBalance_del(BSTNode<ElemType>* &T){BSTNode<ElemType>* lchild = T->child[0];switch(lchild->bf){ case LH:T->bf = EH; lchild->bf = EH; rotateT(T, 1);break;case EH:T->bf = LH;lchild->bf = EH; rotateT(T, 1);break;case RH://这是上面配图的情况BSTNode<ElemType>* rdchild = lchild->child[1];switch(rdchild->bf){ case LH:T->bf = RH;lchild->bf = rdchild->bf = EH;break;case EH:rdchild->bf = T->bf = lchild->bf = EH; break;case RH:T->bf = rdchild->bf = EH;lchild->bf = LH; break;}rotateT(T->child[0], 0);rotateT(T, 1);break;}
}template <typename ElemType>
void AVL<ElemType>::rightBalance_del(BSTNode<ElemType>* &T){BSTNode<ElemType>* rchild = T->child[1];BSTNode<ElemType>* ldchild = rchild->child[0];switch(rchild->bf){ case LH:switch(ldchild->bf){ case LH:ldchild->bf = T->bf = EH; rchild->bf = RH;break;case EH:ldchild->bf = T->bf = rchild->bf = EH; break;case RH:rchild->bf = T->bf = EH; ldchild->bf = LH;break;}rotateT(T->child[1], 1);rotateT(T, 0);break;case EH://outT(this->T);e EH:T->bf = RH;rchild->bf = EH; rotateT(T, 0);break;case RH:T->bf = EH; rchild->bf = EH; rotateT(T, 0);break;}
}int main(){AVL<int> avl;avl.buildT();cout<<"平衡二叉树先序遍历如下:"<<endl;avl.outT(avl.T);cout<<endl;bool shorter = false;avl.deleteAVL(avl.T, 24, shorter);avl.outT(avl.T);return 0;
} /*13 24 37 90 53 013 24 37 90 53 12 26 0
*/

 

转载于:https://www.cnblogs.com/hujunzheng/p/4669058.html

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/531453.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

（六）C语言之函数

（六）C语言之函数

本篇文章分为三个部分讲解&#xff0c;分别为函数、局部变量和全局变量、c语言存储分区 &#xff08;一&#xff09;函数的定义和调用 函数&#xff1a;工程中最小的单位&#xff0c;为了实现某一功能的 函数的定义&#xff1a; 数据类型 函数名(数据类型 形参1&#xff0c;…
阅读更多...
堆排序算法---属于选择排序

堆排序算法---属于选择排序

1.堆 堆实际上是一棵完全二叉树&#xff0c;其任何一非叶节点满足性质&#xff1a; Key[i]<key[2i1]&&Key[i]<key[2i2]或者Key[i]>Key[2i1]&&key>key[2i2] 即任何一非叶节点的关键字不大于或者不小于其左右孩子节点的关键字。 堆分为大顶堆和小顶堆…
阅读更多...
（七）C语言之指针

（七）C语言之指针

c语言相比其他高级语言来说&#xff0c;更接近于对计算机硬件的操作&#xff0c;而指针的应用更是为我们对硬件的操作插上了翅膀&#xff0c;所以指针是嵌入式编程不可少的一部分&#xff0c;在一定意义上说&#xff0c;指针是c语言的精髓。 一、 什么是指针 在计算机中&#…
阅读更多...
（八）C语言之结构

（八）C语言之结构

今天来说一下C语言里的结构体(struct)、共用体(l联合体)union、枚举。 &#xff08;一&#xff09;结构体&#xff1a;struct 1.1 概念 是一种自定义的数据类型结构体是构造类型的一种不同数据类型的集合地址空间连续&#xff0c;每次分配最大数据类型的宽度占用内存为所有变…
阅读更多...
插入排序之表插入排序

插入排序之表插入排序

1.表插入排序只是求得一个有序的链表&#xff0c;它是修改指针的值来代替移动记录&#xff0c;操作过程如下 2.但是这样只能进行顺序查找&#xff0c;不能进行随机查找&#xff0c;为了能实现有序表的折半查找&#xff0c;需要对记录进行重新排列。操作过程如下&#xff1a; 3.…
阅读更多...
电容降压LED驱动电路

电容降压LED驱动电路

电容降压电路具有体积小、成本低、电流相对稳定等优点&#xff0c;可应用于小功率的LED驱动电路中&#xff0c;本文主要介绍了电容降压电路的基本电路 图一&#xff1a; 电容降压式简易电源的基本原理如图一所示&#xff0c;C3为降压电容器&#xff1b;D4为半波整流二极管&…
阅读更多...
延时电路分析

延时电路分析

延时电路经常会用到&#xff0c;RC电路是比较简单的电路。在电路设计中经常会用到将电阻和电容正极连接&#xff0c;电阻另一端接上电源&#xff0c;电容负极接地。 简单的延时电路 上面就是延时的电路图了&#xff0c;延时的时间为T-ln((VCC-Vout)/VCC)RC&#xff0c;公式中的…
阅读更多...
恒流电路的分析(一)

恒流电路的分析(一)

在这里分析一个简单的LED恒流电路&#xff0c;软件采用Multisim进行波形采集 一、元器件 R1为80KΩ左右的金属膜电阻&#xff1b;Q选取耐压值超过350V的VPN三极管&#xff1b;D选取2V左右的稳压二极管(如1N4680)&#xff1b;C2选取10V、100UF以上的电解电容&#xff1b;R2选择…
阅读更多...
ST-LINK USB communication error解决方法

ST-LINK USB communication error解决方法

今天在用stlink-v2下载程序时出现ST-LINK USB communication error&#xff0c;突然就出现了这个问题&#xff0c;在网上找了好多解决办法都不可以用&#xff0c;下面给出我的解决方案&#xff0c;文章末尾给出了网上的几种解决办法&#xff0c;仅供参考。 第一步&#xff1a;找…
阅读更多...
利用STM32制作红外测温仪之硬件设计

利用STM32制作红外测温仪之硬件设计

最近受疫情的影响详细大家都在家里没事干&#xff0c;这里利用stm32最小系统做一个红外测温仪 这篇教程里我们来制作红外测温仪需要用到的硬件&#xff0c;关于PCB的工程文件&#xff0c;后文会给出。 &#xff08;一&#xff09;系统分析 由于我们的功能比较单一&#xff0c;…
阅读更多...
如何在博客中插入背景音乐

如何在博客中插入背景音乐

1.首先进入网音乐官方网站&#xff1b; 2.查找自己喜欢的歌&#xff0c;看到如下界面 3.点击"生成外链播放器" 4.看到下面的html代码了吗&#xff1f;将代码进行复制。 5.进入博客园&#xff0c;点击 "管理" ->"设置"&#xff0c; 将代码复制…
阅读更多...
常用存储器介绍

常用存储器介绍

注意&#xff1a;"易失/非易失"是指存储器断电后&#xff0c;它存储的数据内容是否会丢失的特性。 &#xff08;一&#xff09;RAM和ROM 1.1 RAM RAM即随机存储器&#xff0c;它是指存储器中的数据被读入或者写入与信息所在位置无关&#xff0c;时间都是相同的 1…
阅读更多...
TortoiseGit与github实现项目的上传

TortoiseGit与github实现项目的上传

1. 下载并安装相关软件 这里主要涉及的软件包括msysgit和TortoiseGit。 msysgit的下载地址&#xff1a;http://msysgit.googlecode.com/files/Git-1.7.4-preview20110204.exe TortoiseGit的下载地址&#xff1a;http://code.google.com/p/tortoisegit/downloads/list&#xff0…
阅读更多...
uboot启动流程分析

uboot启动流程分析

Uboot的启动流程分为两个阶段&#xff0c;第一阶段主要是汇编语言编写&#xff0c;第二阶段是C语言编写&#xff0c;每个阶段所做的工作不同&#xff0c;这篇文章分析的是uboot 2010版&#xff0c;以tiny4412的uboot为例。 启动过程涉及的主要文件&#xff1a; arch/arm/cpu/a…
阅读更多...
（二）linux内核镜像制作

（二）linux内核镜像制作

&#xff08;一&#xff09;目的 在进行嵌入式开发的时候&#xff0c;我们往往会先在电脑上安装交叉编译器&#xff0c;然后编译目标板上的代码&#xff0c;最后把代码下载到电路板中&#xff0c;嵌入式系统组成包括&#xff1a;BootLoaderkernelfilesystemapplication&#x…
阅读更多...
js+css实现骰子的随机转动

js+css实现骰子的随机转动

网上找的例子&#xff0c;然后增添了新的东西&#xff0c;在这里展示一下...... 效果图预览&#xff1a; <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html x…
阅读更多...
linux的mount和umount指令使用

linux的mount和umount指令使用

mount即挂在操作&#xff0c;磁盘或分区创建好文件系统后需要挂载到一个目录&#xff08;一般mount在/mnt下&#xff09;才能使 用&#xff0c;和winsdows不同的是在linux下需要手动挂载。 用法&#xff1a;mount [-t文件系统] [选项] 设备目录注意&#xff1a;[ ]为可选项…
阅读更多...
斐波那契的四种求法

斐波那契的四种求法

首先看一下斐波那契的矩阵表示&#xff1a; 数列的递推公式为&#xff1a;f(1)1&#xff0c;f(2)2&#xff0c;f(n)f(n-1)f(n-2)(n>3) 用矩阵表示为&#xff1a; 进一步&#xff0c;可以得出直接推导公式&#xff1a; #include<iostream> #include<cstring> #i…
阅读更多...
利用STM32制作红外测温仪之软件设计(MLX90614)

利用STM32制作红外测温仪之软件设计(MLX90614)

目录&#xff08;一&#xff09;工程目录如图&#xff1a;&#xff08;二&#xff09;main函数实现&#xff1a;&#xff08;三&#xff09;MLX90614测温代码实现前面介绍了使用 STM32制作红外测温仪硬件设计,今天来说一下软件的实现&#xff0c;具体的程序&#xff0c;完整的k…
阅读更多...
Windows下使用Dev-C++开发基于pthread.h的多线程程序

Windows下使用Dev-C++开发基于pthread.h的多线程程序

一、下载Windows版本的pthread 目前最新版本是&#xff1a;pthreads-w32-2-9-1-release.zip。 二、解压pthread到指定目录 我选择的目录是&#xff1a;E:\DEV-CPP\Pthread完成后&#xff0c;该目录会多出三个文件夹&#xff1a;Pre-built.2&#xff0c;pthreads.2&#xff0c;Q…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023