长短期记忆(LSTM)
LSTM 中引入了3个门,即
- 输入门(input gate)
- 遗忘门(forget gate)
- 输出门(output gate)
- 以及与隐藏状态形状相同的记忆细胞(某些文献把记忆细胞当成一种特殊的隐藏状态),从而记录额外的信息。
输入门、遗忘门和输出门
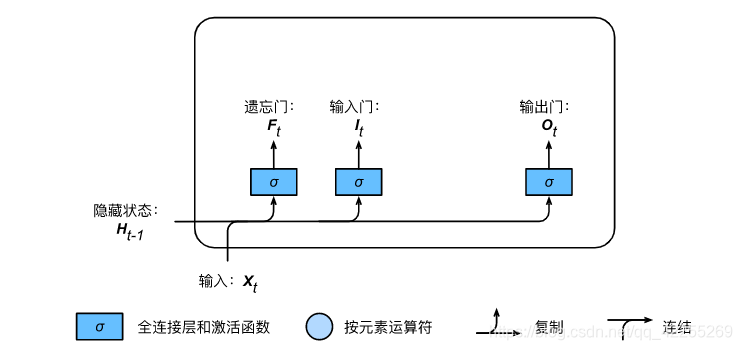
与门控循环单元中的重置门和更新门一样,如下图所示
- 长短期记忆的门的输入均为当前时间步输入Xt\boldsymbol{X}_tXt与上一时间步隐藏状态Ht−1\boldsymbol{H}_{t-1}Ht−1
- 输出由激活函数为sigmoid函数的全连接层计算得到。
- 这3个门元素的值域均为[0,1][0,1][0,1]。
假设
- 隐藏单元个数为hhh
- 给定时间步ttt的小批量输入Xt∈Rn×d\boldsymbol{X}_t \in \mathbb{R}^{n \times d}Xt∈Rn×d(样本数为nnn,输入个数为ddd)
- 上一时间步隐藏状态Ht−1∈Rn×h\boldsymbol{H}_{t-1} \in \mathbb{R}^{n \times h}Ht−1∈Rn×h。
时间步ttt的输入门It∈Rn×h\boldsymbol{I}_t \in \mathbb{R}^{n \times h}It∈Rn×h、遗忘门Ft∈Rn×h\boldsymbol{F}_t \in \mathbb{R}^{n \times h}Ft∈Rn×h和输出门Ot∈Rn×h\boldsymbol{O}_t \in \mathbb{R}^{n \times h}Ot∈Rn×h分别计算如下:
It=σ(XtWxi+Ht−1Whi+bi),Ft=σ(XtWxf+Ht−1Whf+bf),Ot=σ(XtWxo+Ht−1Who+bo),\begin{aligned} \boldsymbol{I}_t &= \sigma(\boldsymbol{X}_t \boldsymbol{W}_{xi} + \boldsymbol{H}_{t-1} \boldsymbol{W}_{hi} + \boldsymbol{b}_i),\\ \boldsymbol{F}_t &= \sigma(\boldsymbol{X}_t \boldsymbol{W}_{xf} + \boldsymbol{H}_{t-1} \boldsymbol{W}_{hf} + \boldsymbol{b}_f),\\ \boldsymbol{O}_t &= \sigma(\boldsymbol{X}_t \boldsymbol{W}_{xo} + \boldsymbol{H}_{t-1} \boldsymbol{W}_{ho} + \boldsymbol{b}_o), \end{aligned} ItFtOt=σ(XtWxi+Ht−1Whi+bi),=σ(XtWxf+Ht−1Whf+bf),=σ(XtWxo+Ht−1Who+bo),
其中
- Wxi,Wxf,Wxo∈Rd×h\boldsymbol{W}_{xi}, \boldsymbol{W}_{xf}, \boldsymbol{W}_{xo} \in \mathbb{R}^{d \times h}Wxi,Wxf,Wxo∈Rd×h和Whi,Whf,Who∈Rh×h\boldsymbol{W}_{hi}, \boldsymbol{W}_{hf}, \boldsymbol{W}_{ho} \in \mathbb{R}^{h \times h}Whi,Whf,Who∈Rh×h是权重参数
- bi,bf,bo∈R1×h\boldsymbol{b}_i, \boldsymbol{b}_f, \boldsymbol{b}_o \in \mathbb{R}^{1 \times h}bi,bf,bo∈R1×h是偏差参数。
候选记忆细胞
接下来,长短期记忆需要计算候选记忆细胞C~t\tilde{\boldsymbol{C}}_tC~t。它的计算与上面介绍的3个门类似,但使用了值域在[−1,1][-1, 1][−1,1]的tanh函数作为激活函数,如下图所示。
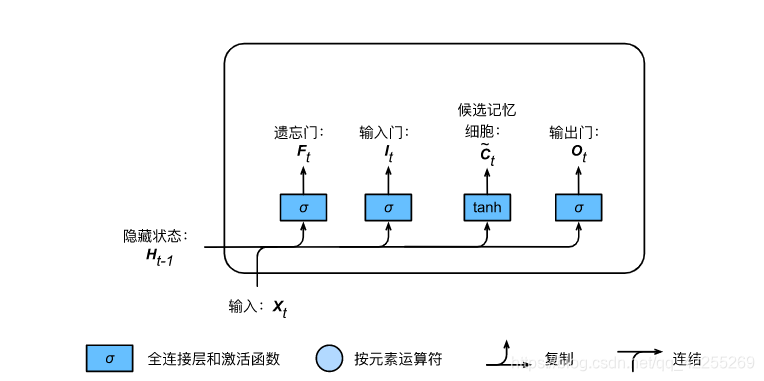
具体来说,时间步ttt的候选记忆细胞C~t∈Rn×h\tilde{\boldsymbol{C}}_t \in \mathbb{R}^{n \times h}C~t∈Rn×h的计算为
C~t=tanh(XtWxc+Ht−1Whc+bc),\tilde{\boldsymbol{C}}_t = \text{tanh}(\boldsymbol{X}_t \boldsymbol{W}_{xc} + \boldsymbol{H}_{t-1} \boldsymbol{W}_{hc} + \boldsymbol{b}_c), C~t=tanh(XtWxc+Ht−1Whc+bc),
其中Wxc∈Rd×h\boldsymbol{W}_{xc} \in \mathbb{R}^{d \times h}Wxc∈Rd×h和Whc∈Rh×h\boldsymbol{W}_{hc} \in \mathbb{R}^{h \times h}Whc∈Rh×h是权重参数,bc∈R1×h\boldsymbol{b}_c \in \mathbb{R}^{1 \times h}bc∈R1×h是偏差参数。
记忆细胞
可以通过元素值域在[0,1][0, 1][0,1]的输入门、遗忘门和输出门来控制隐藏状态中信息的流动,这一般也是通过使用按元素乘法(符号为⊙\odot⊙)来实现的。当前时间步记忆细胞Ct∈Rn×h\boldsymbol{C}_t \in \mathbb{R}^{n \times h}Ct∈Rn×h的计算组合了上一时间步记忆细胞和当前时间步候选记忆细胞的信息,并通过遗忘门和输入门来控制信息的流动:
Ct=Ft⊙Ct−1+It⊙C~t.\boldsymbol{C}_t = \boldsymbol{F}_t \odot \boldsymbol{C}_{t-1} + \boldsymbol{I}_t \odot \tilde{\boldsymbol{C}}_t.Ct=Ft⊙Ct−1+It⊙C~t.
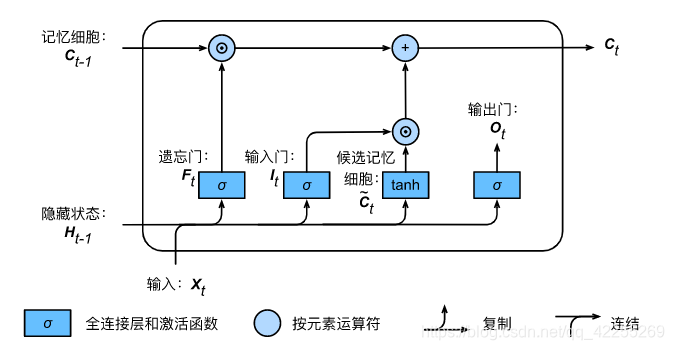
如下图所示
- 遗忘门控制上一时间步的记忆细胞Ct−1\boldsymbol{C}_{t-1}Ct−1中的信息是否传递到当前时间步,而输入门则控制当前时间步的输入Xt\boldsymbol{X}_tXt通过候选记忆细胞C~t\tilde{\boldsymbol{C}}_tC~t如何流入当前时间步的记忆细胞。
- 如果遗忘门一直近似1且输入门一直近似0,过去的记忆细胞将一直通过时间保存并传递至当前时间步。
- 这个设计可以应对循环神经网络中的梯度衰减问题,并更好地捕捉时间序列中时间步距离较大的依赖关系。
隐藏状态
有了记忆细胞以后,接下来我们还可以通过输出门来控制从记忆细胞到隐藏状态Ht∈Rn×h\boldsymbol{H}_t \in \mathbb{R}^{n \times h}Ht∈Rn×h的信息的流动:
Ht=Ot⊙tanh(Ct).\boldsymbol{H}_t = \boldsymbol{O}_t \odot \text{tanh}(\boldsymbol{C}_t).Ht=Ot⊙tanh(Ct).
- 这里的tanh函数确保隐藏状态元素值在-1到1之间。
- 当输出门近似1时,记忆细胞信息将传递到隐藏状态供输出层使用
- 当输出门近似0时,记忆细胞信息只自己保留。
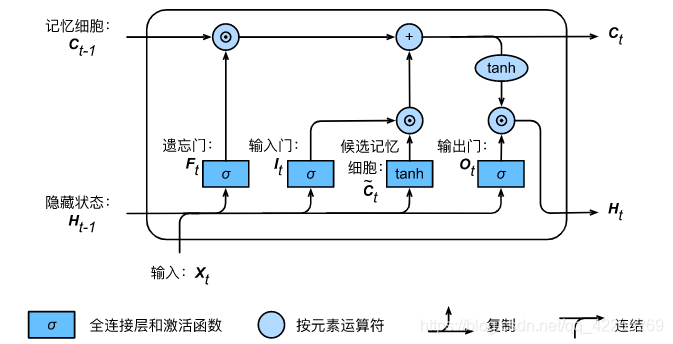
下图展示了长短期记忆中隐藏状态的计算。
实现LSTM网络
读取数据集
import numpy as np
import torch
from torch import nn, optim
import torch.nn.functional as Fimport sys
sys.path.append("..")
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')def load_data_jay_lyrics():"""加载周杰伦歌词数据集"""with zipfile.ZipFile('../../data/jaychou_lyrics.txt.zip') as zin:with zin.open('jaychou_lyrics.txt') as f:corpus_chars = f.read().decode('utf-8')corpus_chars = corpus_chars.replace('\n', ' ').replace('\r', ' ')corpus_chars = corpus_chars[0:10000]idx_to_char = list(set(corpus_chars))char_to_idx = dict([(char, i) for i, char in enumerate(idx_to_char)])vocab_size = len(char_to_idx)corpus_indices = [char_to_idx[char] for char in corpus_chars]return corpus_indices, char_to_idx, idx_to_char, vocab_size(corpus_indices, char_to_idx, idx_to_char, vocab_size) = load_data_jay_lyrics()
初始化模型参数
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
print('will use', device)def get_params():def _one(shape):ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32)return torch.nn.Parameter(ts, requires_grad=True)def _three():return (_one((num_inputs, num_hiddens)),_one((num_hiddens, num_hiddens)),torch.nn.Parameter(torch.zeros(num_hiddens, device=device, dtype=torch.float32), requires_grad=True))W_xi, W_hi, b_i = _three() # 输入门参数W_xf, W_hf, b_f = _three() # 遗忘门参数W_xo, W_ho, b_o = _three() # 输出门参数W_xc, W_hc, b_c = _three() # 候选记忆细胞参数# 输出层参数W_hq = _one((num_hiddens, num_outputs))b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device, dtype=torch.float32), requires_grad=True)return nn.ParameterList([W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q])
定义模型
def init_lstm_state(batch_size, num_hiddens, device):return (torch.zeros((batch_size, num_hiddens), device=device), torch.zeros((batch_size, num_hiddens), device=device))
下面根据长短期记忆的计算表达式定义模型
- 只有隐藏状态会传递到输出层,而记忆细胞不参与输出层的计算。
def lstm(inputs, state, params):[W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q] = params(H, C) = stateoutputs = []for X in inputs:I = torch.sigmoid(torch.matmul(X, W_xi) + torch.matmul(H, W_hi) + b_i)F = torch.sigmoid(torch.matmul(X, W_xf) + torch.matmul(H, W_hf) + b_f)O = torch.sigmoid(torch.matmul(X, W_xo) + torch.matmul(H, W_ho) + b_o)C_tilda = torch.tanh(torch.matmul(X, W_xc) + torch.matmul(H, W_hc) + b_c)C = F * C + I * C_tildaH = O * C.tanh()Y = torch.matmul(H, W_hq) + b_qoutputs.append(Y)return outputs, (H, C)
训练模型并创作歌词
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']def train_and_predict_rnn(rnn, get_params, init_rnn_state, num_hiddens,vocab_size, device, corpus_indices, idx_to_char,char_to_idx, is_random_iter, num_epochs, num_steps,lr, clipping_theta, batch_size, pred_period,pred_len, prefixes):if is_random_iter:data_iter_fn = data_iter_randomelse:data_iter_fn = data_iter_consecutiveparams = get_params()loss = nn.CrossEntropyLoss()for epoch in range(num_epochs):if not is_random_iter: # 如使用相邻采样,在epoch开始时初始化隐藏状态state = init_rnn_state(batch_size, num_hiddens, device)l_sum, n, start = 0.0, 0, time.time()data_iter = data_iter_fn(corpus_indices, batch_size, num_steps, device)for X, Y in data_iter:if is_random_iter: # 如使用随机采样,在每个小批量更新前初始化隐藏状态state = init_rnn_state(batch_size, num_hiddens, device)else: # 否则需要使用detach函数从计算图分离隐藏状态, 这是为了# 使模型参数的梯度计算只依赖一次迭代读取的小批量序列(防止梯度计算开销太大)for s in state:s.detach_()inputs = to_onehot(X, vocab_size)# outputs有num_steps个形状为(batch_size, vocab_size)的矩阵(outputs, state) = rnn(inputs, state, params)# 拼接之后形状为(num_steps * batch_size, vocab_size)outputs = torch.cat(outputs, dim=0)# Y的形状是(batch_size, num_steps),转置后再变成长度为# batch * num_steps 的向量,这样跟输出的行一一对应y = torch.transpose(Y, 0, 1).contiguous().view(-1)# 使用交叉熵损失计算平均分类误差l = loss(outputs, y.long())# 梯度清0if params[0].grad is not None:for param in params:param.grad.data.zero_()l.backward()grad_clipping(params, clipping_theta, device) # 裁剪梯度sgd(params, lr, 1) # 因为误差已经取过均值,梯度不用再做平均l_sum += l.item() * y.shape[0]n += y.shape[0]if (epoch + 1) % pred_period == 0:print('epoch %d, perplexity %f, time %.2f sec' % (epoch + 1, math.exp(l_sum / n), time.time() - start))for prefix in prefixes:print(' -', predict_rnn(prefix, pred_len, rnn, params, init_rnn_state,num_hiddens, vocab_size, device, idx_to_char, char_to_idx))train_and_predict_rnn(lstm, get_params, init_lstm_state, num_hiddens,vocab_size, device, corpus_indices, idx_to_char,char_to_idx, False, num_epochs, num_steps, lr,clipping_theta, batch_size, pred_period, pred_len,prefixes)
深度循环神经网络)
双向循环神经网络)












)




