深度学习与优化算法原理

优化函数与深度学习

• 在一个深度学习问题中，通常需要预先定义一个损失函数。
• 有了损失函数以后，使用优化算法试图将其最小化。

在优化中，这样的损失函数通常被称作优化问题的目标函数（objective function）。

• 依据惯例，优化算法通常只考虑最小化目标函数。
• 其实，任何最大化问题都可以很容易地转化为最小化问题，只需令目标函数的相反数为新的目标函数即可。

虽然优化为深度学习提供了最小化损失函数的方法，但本质上，优化与深度学习的目标是有区别的。

训练误差和泛化误差是不同的：

• 优化算法的目标函数通常是一个基于训练数据集的损失函数，优化的目标在于降低训练误差。
• 而深度学习的目标在于降低泛化误差。为了降低泛化误差，除了使用优化算法降低训练误差以外，还需要注意应对过拟合。

深度学习优化的问题

深度学习中绝大多数目标函数都很复杂。因此，很多优化问题并不存在解析解，而需要使用基于数值方法的优化算法找到近似解，即数值解。为了求得最小化目标函数的数值解，我们将通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。

常见的优化在深度学习中的挑战，有局部最小值和鞍点等。

局部最小值

对于目标函数$f(x)$，如果$f(x)$在$x$上的值比在$x$邻近的其他点的值更小，那么$f(x)$可能是一个局部最小值（local minimum）。如果$f(x)$在$x$上的值是目标函数在整个定义域上的最小值，那么$f(x)$是全局最小值（global minimum）。

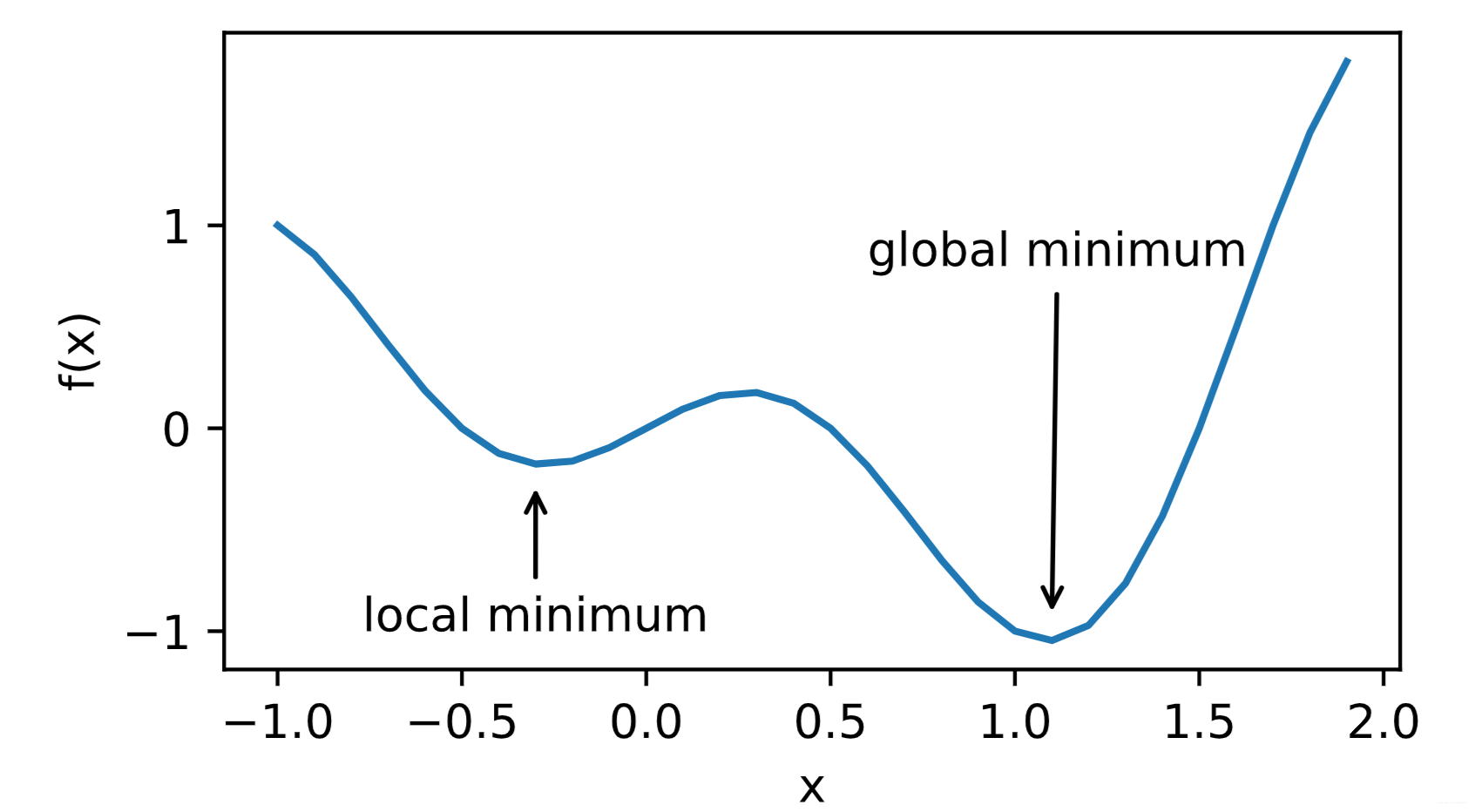
举个例子，给定函数

$$f(x)=x\cdot \text{cos}(\pi x),-1.0\le x\le 2.0,$$

我们可以大致找出该函数的局部最小值和全局最小值的位置。需要注意的是，图中箭头所指示的只是大致位置。

%matplotlib inline
import sys
sys.path.append("..") 
from mpl_toolkits import mplot3d # 三维画图
from matplotlib import pyplot as plt
import numpy as npdef f(x):return x * np.cos(np.pi * x)def set_figsize(figsize=(3.5, 2.5)):use_svg_display()# 设置图的尺寸plt.rcParams['figure.figsize'] = figsize

set_figsize((4.5, 2.5))
x = np.arange(-1.0, 2.0, 0.1)
fig,  = plt.plot(x, f(x))
fig.axes.annotate('local minimum', xy=(-0.3, -0.25), xytext=(-0.77, -1.0),arrowprops=dict(arrowstyle='->'))
fig.axes.annotate('global minimum', xy=(1.1, -0.95), xytext=(0.6, 0.8),arrowprops=dict(arrowstyle='->'))
plt.xlabel('x')
plt.ylabel('f(x)');

深度学习模型的目标函数可能有若干局部最优值。当一个优化问题的数值解在局部最优解附近时

• 由于目标函数有关解的梯度接近或变成零
• 最终迭代求得的数值解可能只令目标函数局部最小化而非全局最小化

鞍点

梯度接近或变成零可能是由于当前解在局部最优解附近造成的，另一种可能性是当前解在鞍点（saddle point）附近。

例如，给定函数

$$f(x)=x^3,$$

我们可以找出该函数的鞍点位置。

x = np.arange(-2.0, 2.0, 0.1)
fig, = plt.plot(x, x**3)
fig.axes.annotate('saddle point', xy=(0, -0.2), xytext=(-0.52, -5.0),arrowprops=dict(arrowstyle='->'))
plt.xlabel('x')
plt.ylabel('f(x)');

又例如下面这个定义在二维空间的函数的例子，

$$f(x,y)=x^2-y^2.$$

我们可以找出该函数的鞍点位置。

x, y = np.mgrid[-1: 1: 31j, -1: 1: 31j]
z = x**2 - y**2ax = plt.figure().add_subplot(111, projection='3d')
ax.plot_wireframe(x, y, z, **{'rstride': 2, 'cstride': 2})
ax.plot([0], [0], [0], 'rx')
ticks = [-1,  0, 1]
plt.xticks(ticks)
plt.yticks(ticks)
ax.set_zticks(ticks)
plt.xlabel('x')
plt.ylabel('y');

• 该函数看起来像一个马鞍，而鞍点恰好是马鞍上可坐区域的中心
• 在图的鞍点位置，目标函数在$x$轴方向上是局部最小值，但在$y$轴方向上是局部最大值。

假设一个函数的输入为$k$维向量，输出为标量，那么它的海森矩阵（Hessian matrix）有$k$个特征值。该函数在梯度为0的位置上可能是局部最小值、局部最大值或者鞍点。

• 当函数的海森矩阵在梯度为零的位置上的特征值全为正时，该函数得到局部最小值。
• 当函数的海森矩阵在梯度为零的位置上的特征值全为负时，该函数得到局部最大值。
• 当函数的海森矩阵在梯度为零的位置上的特征值有正有负时，该函数得到鞍点。

随机矩阵理论告诉我们，对于一个大的高斯随机矩阵来说，任一特征值是正或者是负的概率都是0.5。那么，以上第一种情况的概率为 $0.5^k$。由于深度学习模型参数通常都是高维的（$k$很大），目标函数的鞍点通常比局部最小值更常见。

在深度学习中，虽然找到目标函数的全局最优解很难，但这并非是必要的。

梯度下降和随机梯度下降

虽然梯度下降在深度学习中很少被直接使用，但理解梯度的意义以及沿着梯度反方向更新自变量可能降低目标函数值的原因是学习后续优化算法的基础。

一维梯度下降

先以简单的一维梯度下降为例。

• 假设连续可导的函数$f:\mathbb{R}\to \mathbb{R}$的输入和输出都是标量
• 给定绝对值足够小的数$ϵ$

根据泰勒展开公式，我们得到以下的近似：

$$f(x+ϵ)\approx f(x)+ϵf^{\prime }(x).$$

这里$f^{\prime }(x)$是函数$f$在$x$处的梯度。一维函数的梯度是一个标量，也称导数。

接下来，找到一个常数$\eta >0$，使得$\left|\eta f^{\prime }(x)\right|$足够小，那么可以将$ϵ$替换为$-\eta f^{\prime }(x)$并得到

$$f(x-\eta f^{\prime }(x))\approx f(x)-\eta f^{\prime }(x{)}^2.$$

如果导数$f^{\prime }(x)\ne 0$，那么$\eta f^{\prime }(x{)}^2>0$，所以

$$f(x-\eta f^{\prime }(x))\lesssim f(x).$$

这意味着，如果通过

$$x\leftarrow x-\eta f^{\prime }(x)$$

来迭代$x$，函数$f(x)$的值可能会降低。因此在梯度下降中，我们先选取一个初始值$x$和常数$\eta >0$，然后不断通过上式来迭代$x$，直到达到停止条件，例如$f^{\prime }(x{)}^2$的值已足够小或迭代次数已达到某个值。

下面以目标函数$f(x)=x^2$为例来看一看梯度下降是如何工作的。虽然很明显最小化$f(x)$的解为$x=0$，这里依然使用这个简单函数来观察$x$是如何被迭代的。

%matplotlib inline
import numpy as np
import torch
import math
import sys
sys.path.append("..") def gd(eta):x = 10results = [x]for i in range(10):x -= eta * 2 * x  # f(x) = x * x的导数为f'(x) = 2 * xresults.append(x)print('epoch 10, x:', x)return resultsres = gd(0.2)

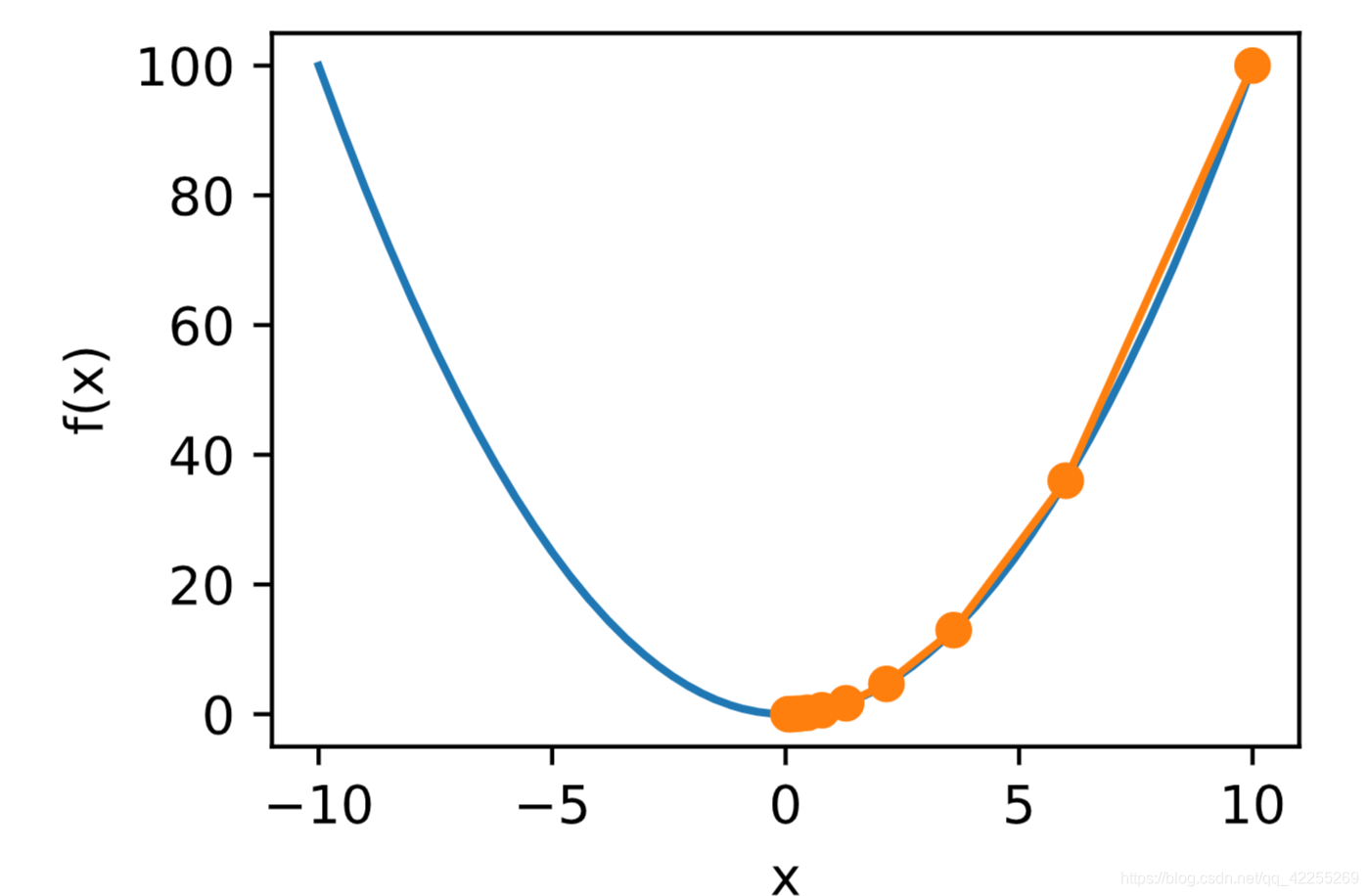
使用$x=10$作为初始值，并设$\eta =0.2$。使用梯度下降对$x$迭代10次，可见最终$x$的值较接近最优解。

绘制出自变量$x$的迭代轨迹：

def show_trace(res):n = max(abs(min(res)), abs(max(res)), 10)f_line = np.arange(-n, n, 0.1)set_figsize()plt.plot(f_line, [x * x for x in f_line])plt.plot(res, [x * x for x in res], '-o')plt.xlabel('x')plt.ylabel('f(x)')show_trace(res)

学习率

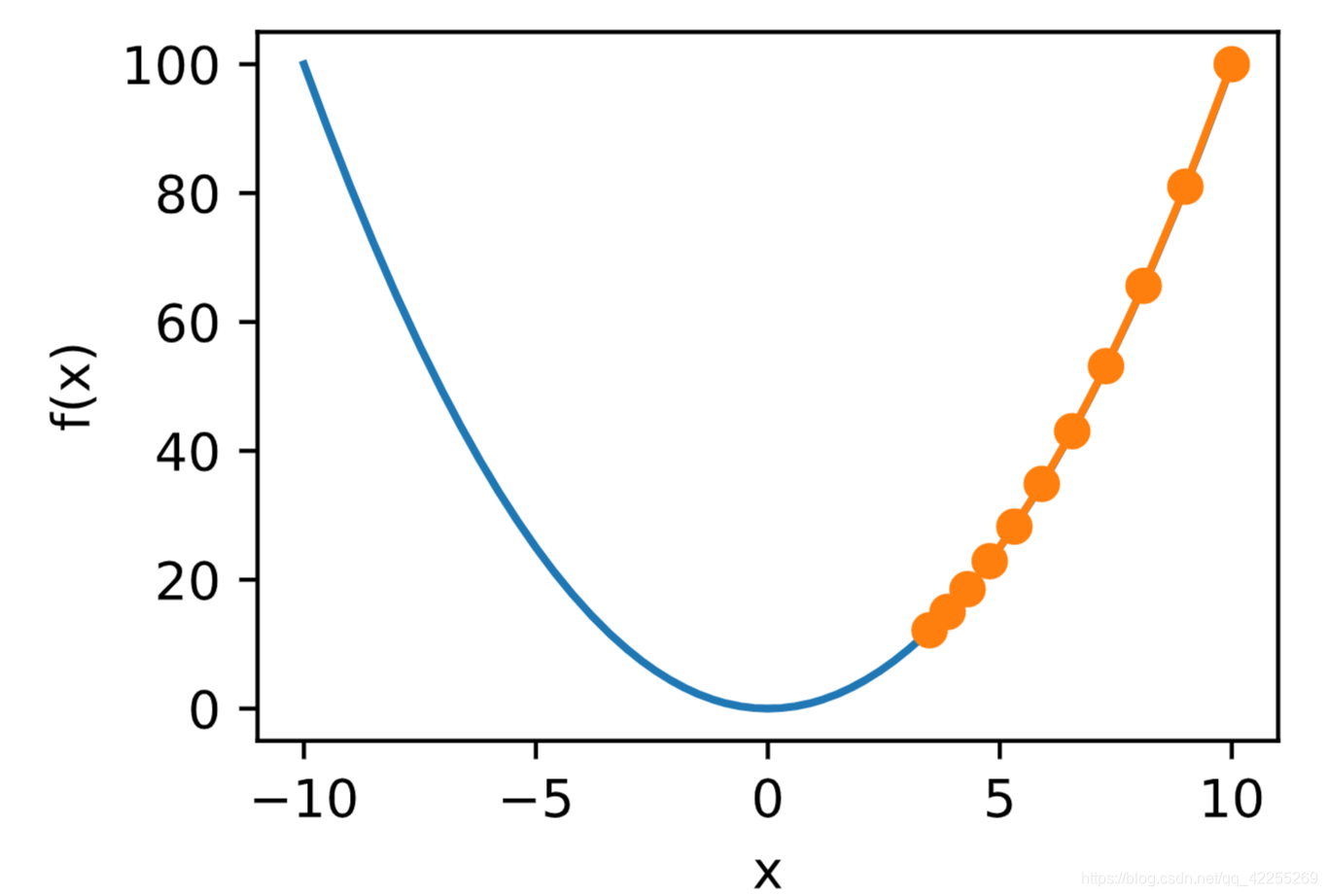
上述梯度下降算法中的正数$\eta$通常叫作学习率。这是一个超参数，需要人工设定。如果使用过小的学习率，会导致$x$更新缓慢从而需要更多的迭代才能得到较好的解。

下面展示使用学习率$\eta =0.05$时自变量$x$的迭代轨迹

show_trace(gd(0.05))

如果使用过大的学习率，$\left|\eta f^{\prime }(x)\right|$可能会过大从而使前面提到的一阶泰勒展开公式不再成立：这时我们无法保证迭代$x$会降低$f(x)$的值。

举个例子，当设学习率$\eta =1.1$时，可以看到$x$不断越过（overshoot）最优解$x=0$并逐渐发散。

show_trace(gd(1.1))

维度增加：多维梯度下降

在了解了一维梯度下降之后，我们再考虑一种更广义的情况：

• 目标函数的输入为向量
• 输出为标量。

假设目标函数$f:{\mathbb{R}}^d\to \mathbb{R}$的输入是一个$d$维向量$\mathbf{x}=[x_1,x_2,\dots ,x_d{]}^{\top }$。目标函数$f(\mathbf{x})$有关$\mathbf{x}$的梯度是一个由$d$个偏导数组成的向量：

$${\nabla }_{\mathbf{x}}f(\mathbf{x})=[\frac{\partial f(\mathbf{x})}{\partial x_1},\frac{\partial f(\mathbf{x})}{\partial x_2},\dots ,\frac{\partial f(\mathbf{x})}{\partial x_d}{]}^{\top }.$$

为表示简洁，我们用$\nabla f(\mathbf{x})$代替${\nabla }_{\mathbf{x}}f(\mathbf{x})$。梯度中每个偏导数元素$\partial f(\mathbf{x})/\partial x_i$代表着$f$在$\mathbf{x}$有关输入$x_i$的变化率。为了测量$f$沿着单位向量$\mathbf{u}$（即$|\mathbf{u}|=1$）方向上的变化率，在多元微积分中，我们定义$f$在$\mathbf{x}$上沿着$\mathbf{u}$方向的方向导数为

$${\text{D}}_{\mathbf{u}}f(\mathbf{x})=\underset{h\to 0}{\lim }\frac{f(\mathbf{x}+h_{\mathbf{u}})-f(\mathbf{x})}{h}.$$

依据方向导数性质，以上方向导数可以改写为

$${\text{D}}_{\mathbf{u}}f(\mathbf{x})=\nabla f(\mathbf{x})\cdot \mathbf{u}(向量相乘)$$

方向导数${\text{D}}_{\mathbf{u}}f(\mathbf{x})$给出了$f$在$\mathbf{x}$上沿着所有可能方向的变化率。为了最小化$f$，我们希望找到$f$能被降低最快的方向。因此，我们可以通过单位向量$\mathbf{u}$来最小化方向导数${\text{D}}_{\mathbf{u}}f(\mathbf{x})$。

由于${\text{D}}_{\mathbf{u}}f(\mathbf{x})=|\nabla f(\mathbf{x})|\cdot |\mathbf{u}|\cdot \text{cos}(\theta )=|\nabla f(\mathbf{x})|\cdot \text{cos}(\theta )$， 其中$\theta$为梯度$\nabla f(\mathbf{x})$和单位向量$\mathbf{u}$之间的夹角，当$\theta =\pi$时，$\text{cos}(\theta )$取得最小值$-1$。因此，当$\mathbf{u}$在梯度方向$\nabla f(\mathbf{x})$的相反方向时，方向导数${\text{D}}_{\mathbf{u}}f(\mathbf{x})$被最小化。因此，我们可能通过梯度下降算法来不断降低目标函数$f$的值：

$$\mathbf{x}\leftarrow \mathbf{x}-\eta \nabla f(\mathbf{x}).$$

同样，其中$\eta$（取正数）称作学习率。

下面我们构造一个目标函数

• 输入为二维向量$\mathbf{x}=[x_1,x_2{]}^{\top }$
• 输出为标量
• $f(\mathbf{x})=x_1^2+2x_2^2$。

那么，梯度$\nabla f(\mathbf{x})=[2x_1,4x_2{]}^{\top }$。我们将观察梯度下降从初始位置$[-5,-2]$开始对自变量$\mathbf{x}$的迭代轨迹。

先定义两个辅助函数，第一个函数使用给定的自变量更新函数，从初始位置$[-5,-2]$开始迭代自变量$\mathbf{x}$共20次，第二个函数对自变量$\mathbf{x}$的迭代轨迹进行可视化。

def train_2d(trainer):  x1, x2, s1, s2 = -5, -2, 0, 0  # s1和s2是自变量状态，本章后续几节会使用results = [(x1, x2)]for i in range(20):x1, x2, s1, s2 = trainer(x1, x2, s1, s2)results.append((x1, x2))print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))return resultsdef show_trace_2d(f, results):  plt.plot(*zip(*results), '-o', color='#ff7f0e')x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')plt.xlabel('x1')plt.ylabel('x2')

然后，观察学习率为0.10.1时自变量的迭代轨迹。使用梯度下降对自变量xx迭代20次后，可见最终xx的值较接近最优解[0,0][0,0]。

eta = 0.1def f_2d(x1, x2):  # 目标函数return x1 ** 2 + 2 * x2 ** 2def gd_2d(x1, x2, s1, s2):return (x1 - eta * 2 * x1, x2 - eta * 4 * x2, 0, 0)show_trace_2d(f_2d, train_2d(gd_2d))

随机梯度下降

在深度学习里，目标函数通常是训练数据集中有关各个样本的损失函数的平均。设$f_i(\mathbf{x})$是有关索引为$i$的训练数据样本的损失函数，$n$是训练数据样本数，$\mathbf{x}$是模型的参数向量，那么目标函数定义为

$$f(\mathbf{x})=\frac{1}{n}\sum _{i=1}^n{f}_i(\mathbf{x}).$$

目标函数在$\mathbf{x}$处的梯度计算为

$$\nabla f(\mathbf{x})=\frac{1}{n}\sum _{i=1}^n\nabla f_i(\mathbf{x}).$$

如果使用梯度下降，每次自变量迭代的计算开销为$\mathcal{O}(n)$，它随着$n$线性增长。因此，当训练数据样本数很大时，梯度下降每次迭代的计算开销很高。

随机梯度下降（stochastic gradient descent，SGD）减少了每次迭代的计算开销。在随机梯度下降的每次迭代中，我们随机均匀采样的一个样本索引$i\in 1,\dots ,n$，并计算梯度$\nabla f_i(\mathbf{x})$来迭代$\mathbf{x}$：

$$\mathbf{x}\leftarrow \mathbf{x}-\eta \nabla f_i(\mathbf{x}).$$

这里$\eta$同样是学习率。可以看到每次迭代的计算开销从梯度下降的$\mathcal{O}(n)$降到了常数$\mathcal{O}(1)$。值得强调的是，随机梯度$\nabla f_i(\mathbf{x})$是对梯度$\nabla f(\mathbf{x})$的无偏估计：

$$E_i\nabla f_i(\mathbf{x})=\frac{1}{n}\sum _{i=1}^n\nabla f_i(\mathbf{x})=\nabla f(\mathbf{x}).$$

这意味着，平均来说，随机梯度是对梯度的一个良好的估计。

下面我们通过在梯度中添加均值为0的随机噪声来模拟随机梯度下降，以此来比较它与梯度下降的区别。

def sgd_2d(x1, x2, s1, s2):return (x1 - eta * (2 * x1 + np.random.normal(0.1)),x2 - eta * (4 * x2 + np.random.normal(0.1)), 0, 0)show_trace_2d(f_2d, train_2d(sgd_2d))

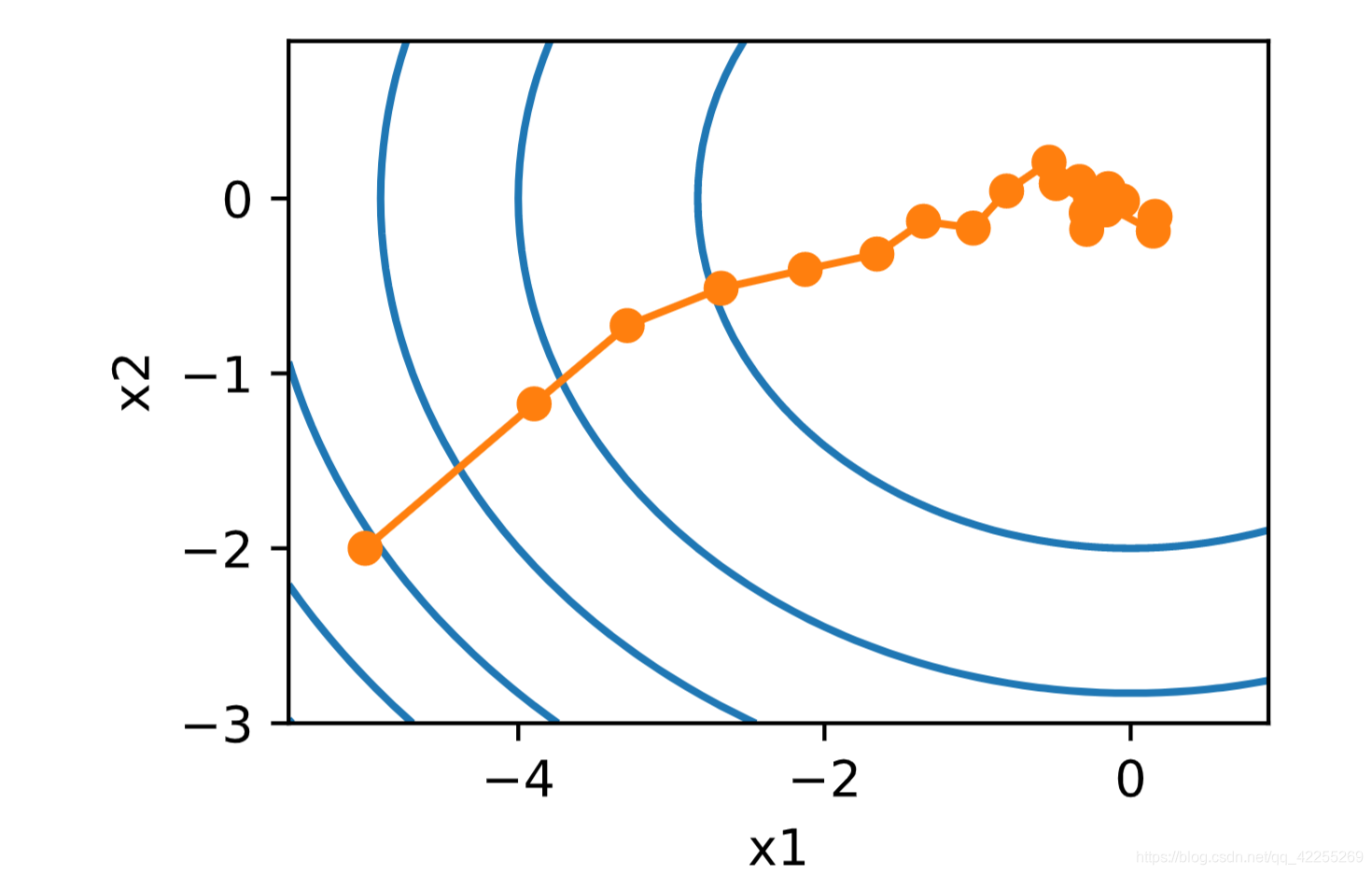
随机梯度下降中自变量的迭代轨迹相对于梯度下降中的来说更为曲折。这是由于实验所添加的噪声使模拟的随机梯度的准确度下降。在实际中，这些噪声通常指训练数据集中的无意义的干扰。