动量法
目标函数有关自变量的梯度代表了目标函数在自变量当前位置下降最快的方向,因此,梯度下降也叫作最陡下降(steepest descent)。在每次迭代中,梯度下降根据自变量当前位置,沿着当前位置的梯度更新自变量。然而,如果自变量的迭代方向仅仅取决于自变量当前位置,这可能会带来一些问题。
梯度下降的问题
考虑一个目标函数:
- 输入为二维向量x=[x1,x2]⊤\boldsymbol{x} = [x_1, x_2]^\topx=[x1,x2]⊤
- 输出为标量
- f(x)=0.1x12+2x22f(\boldsymbol{x})=0.1x_1^2+2x_2^2f(x)=0.1x12+2x22。
这里将x12x_1^2x12系数从111减小到了0.10.10.1。下面实现基于这个目标函数的梯度下降,并演示使用学习率为0.40.40.4时自变量的迭代轨迹。
%matplotlib inline
import sys
sys.path.append("..")
from matplotlib import pyplot as plt
import torcheta = 0.4 # 学习率def f_2d(x1, x2):return 0.1 * x1 ** 2 + 2 * x2 ** 2def gd_2d(x1, x2, s1, s2):return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0, 0)def show_trace_2d(f, results): plt.plot(*zip(*results), '-o', color='#ff7f0e')x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')plt.xlabel('x1')plt.ylabel('x2')def train_2d(trainer): x1, x2, s1, s2 = -5, -2, 0, 0 # s1和s2是自变量状态results = [(x1, x2)]for i in range(20):x1, x2, s1, s2 = trainer(x1, x2, s1, s2)results.append((x1, x2))print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))return resultsshow_trace_2d(f_2d, train_2d(gd_2d))
输出:
epoch 20, x1 -0.943467, x2 -0.000073
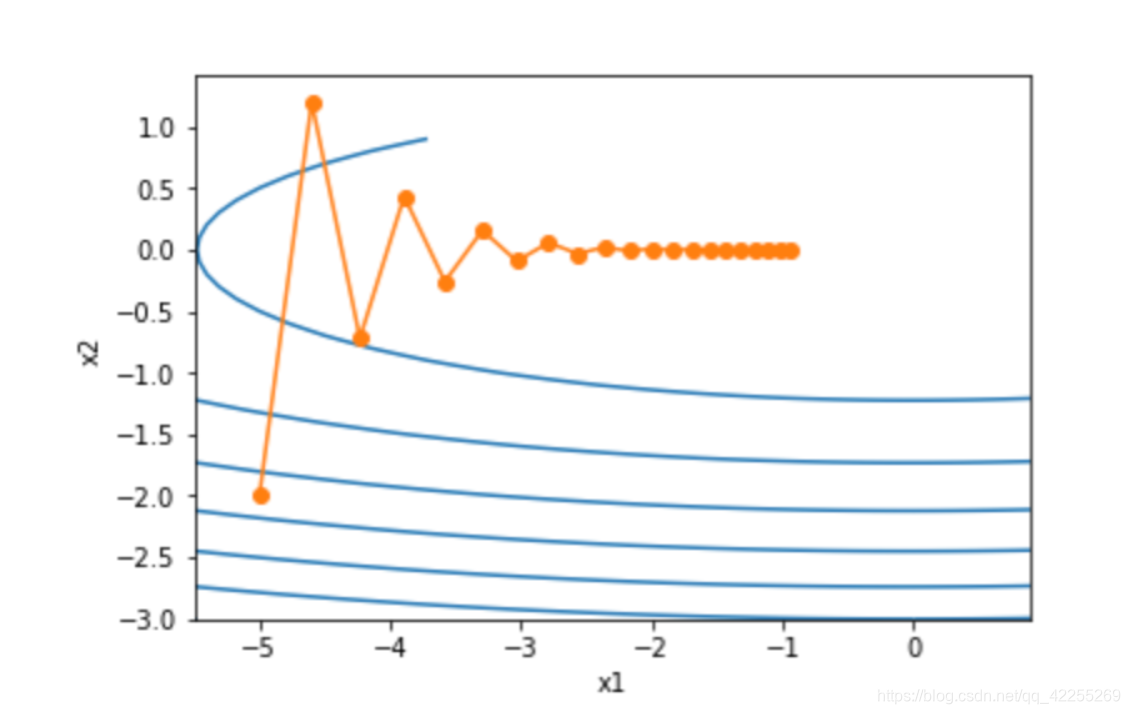
这幅图可以理解为f(x)f(\boldsymbol{x})f(x)在x1x_1x1、x2x_2x2平面上的投影,可以看到
- 同一位置上,目标函数在竖直方向(x2x_2x2轴方向)比在水平方向(x1x_1x1轴方向)的斜率的绝对值更大。
- 因此,给定学习率,梯度下降迭代自变量时会使自变量在竖直方向比在水平方向移动幅度更大。
- 我们需要一个较小的学习率从而避免自变量在竖直方向上越过目标函数最优解。然而,这会造成自变量在水平方向上朝最优解移动变慢。
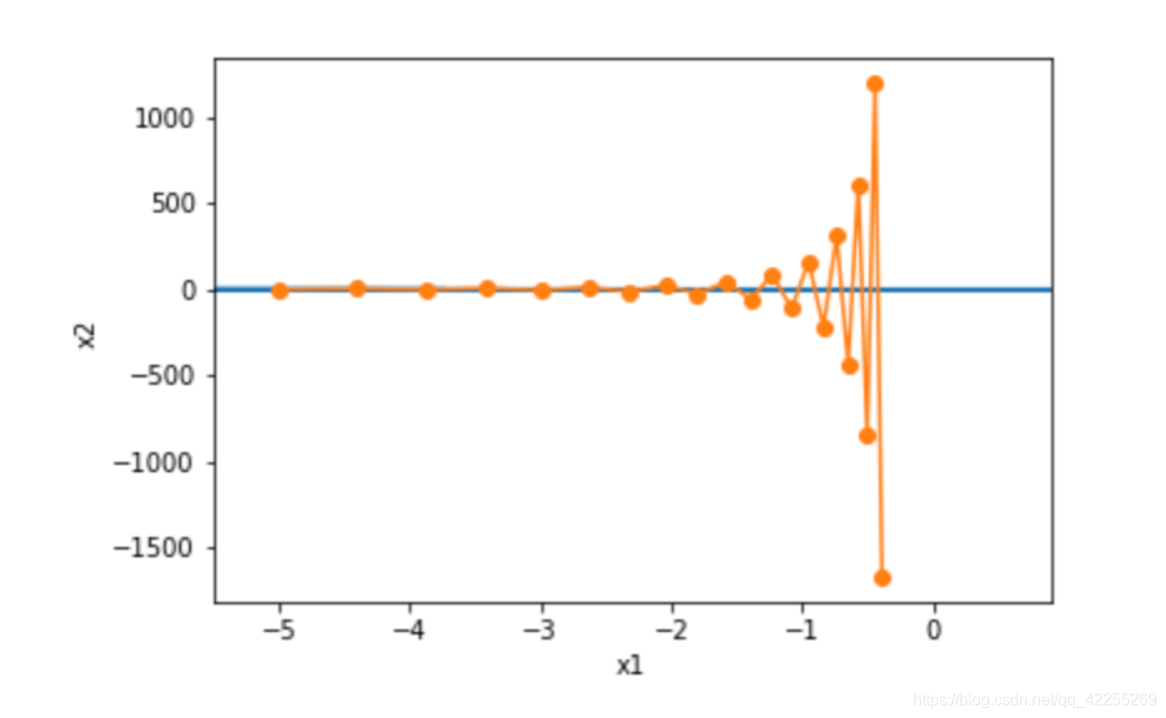
下面我们试着将学习率调得稍大一点,此时自变量在竖直方向不断越过最优解并逐渐发散。
eta = 0.6
show_trace_2d(f_2d, train_2d(gd_2d))
动量法
动量法的提出是为了解决梯度下降的上述问题。
- 设时间步ttt的自变量为xt\boldsymbol{x}_txt
- 学习率为ηt\eta_tηt
- 在时间步000,动量法创建速度变量v0\boldsymbol{v}_0v0,并将其元素初始化成0。在时间步t>0t>0t>0,动量法对每次迭代的步骤做如下修改:
vt←γvt−1+ηtgt,xt←xt−1−vt,\begin{aligned} \boldsymbol{v}_t &\leftarrow \gamma \boldsymbol{v}_{t-1} + \eta_t \boldsymbol{g}_t, \\ \boldsymbol{x}_t &\leftarrow \boldsymbol{x}_{t-1} - \boldsymbol{v}_t, \end{aligned} vtxt←γvt−1+ηtgt,←xt−1−vt,
其中,动量超参数γ\gammaγ满足0≤γ<10 \leq \gamma < 10≤γ<1。当γ=0\gamma=0γ=0时,动量法等价于小批量随机梯度下降。
在解释动量法的数学原理前,让我们先从实验中观察梯度下降在使用动量法后的迭代轨迹。
def momentum_2d(x1, x2, v1, v2):v1 = gamma * v1 + eta * 0.2 * x1v2 = gamma * v2 + eta * 4 * x2return x1 - v1, x2 - v2, v1, v2eta, gamma = 0.4, 0.5
show_trace_2d(f_2d, train_2d(momentum_2d))
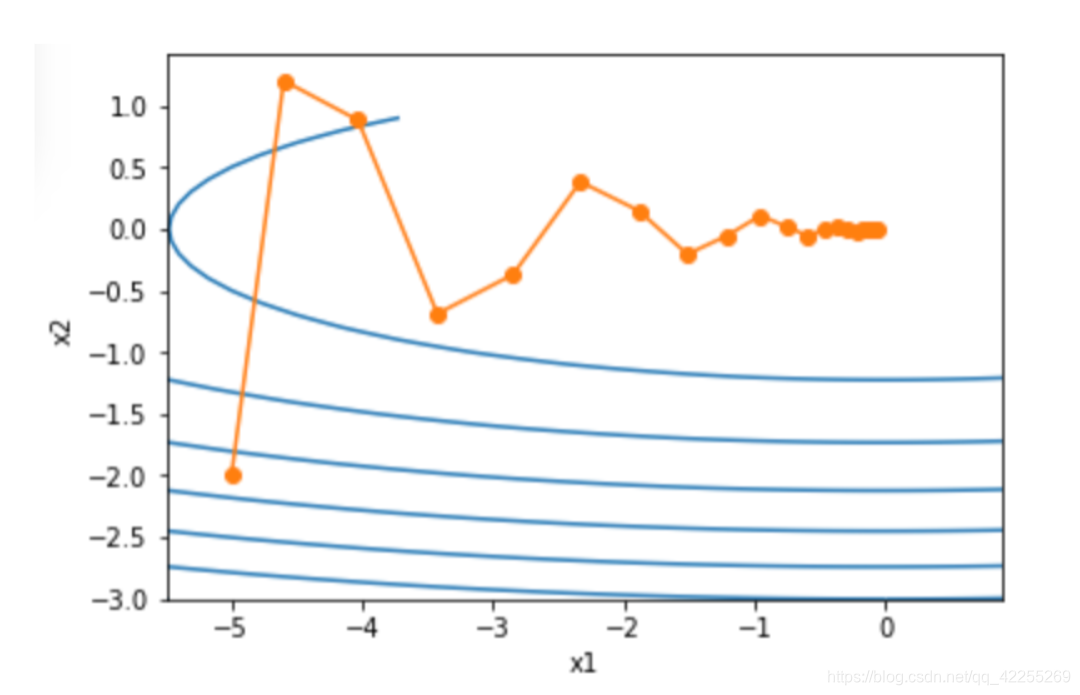
可以看到,使用较小的学习率η=0.4\eta=0.4η=0.4和动量超参数γ=0.5\gamma=0.5γ=0.5时
- 动量法在竖直方向上的移动更加平滑
- 且在水平方向上更快逼近最优解
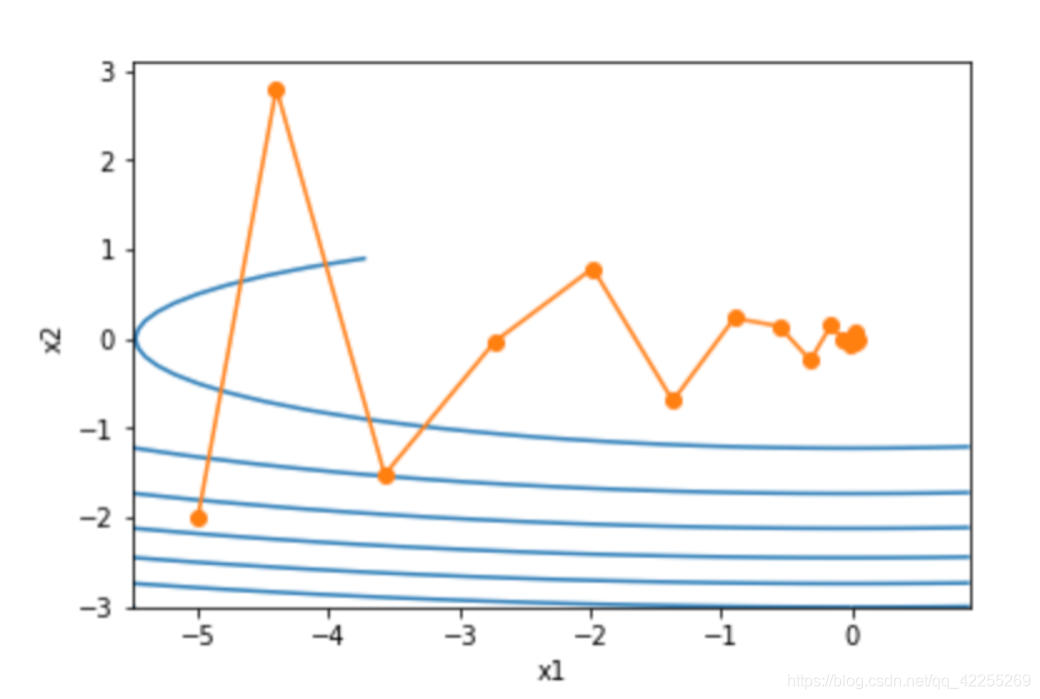
下面使用较大的学习率η=0.6\eta=0.6η=0.6,此时自变量也不再发散。
eta = 0.6
show_trace_2d(f_2d, train_2d(momentum_2d))
指数加权移动平均
为了从数学上理解动量法,需要先解释一下指数加权移动平均(exponentially weighted moving average)。
- 给定超参数0≤γ<10 \leq \gamma < 10≤γ<1
- 当前时间步ttt的变量yty_tyt
- 上一时间步t−1t-1t−1的变量yt−1y_{t-1}yt−1
- 当前时间步另一变量xtx_txt
当前时间步ttt的变量yty_tyt是上一时间步t−1t-1t−1的变量yt−1y_{t-1}yt−1与当前时间步另一变量xtx_txt的线性组合:
yt=γyt−1+(1−γ)xt.y_t = \gamma y_{t-1} + (1-\gamma) x_t.yt=γyt−1+(1−γ)xt.
我们可以对yty_tyt展开:
yt=(1−γ)xt+γyt−1=(1−γ)xt+(1−γ)⋅γxt−1+γ2yt−2=(1−γ)xt+(1−γ)⋅γxt−1+(1−γ)⋅γ2xt−2+γ3yt−3…\begin{aligned} y_t &= (1-\gamma) x_t + \gamma y_{t-1}\\ &= (1-\gamma)x_t + (1-\gamma) \cdot \gamma x_{t-1} + \gamma^2y_{t-2}\\ &= (1-\gamma)x_t + (1-\gamma) \cdot \gamma x_{t-1} + (1-\gamma) \cdot \gamma^2x_{t-2} + \gamma^3y_{t-3}\ &\ldots \end{aligned} yt=(1−γ)xt+γyt−1=(1−γ)xt+(1−γ)⋅γxt−1+γ2yt−2=(1−γ)xt+(1−γ)⋅γxt−1+(1−γ)⋅γ2xt−2+γ3yt−3 …
令n=1/(1−γ)n = 1/(1-\gamma)n=1/(1−γ),那么 (1−1/n)n=γ1/(1−γ)\left(1-1/n\right)^n = \gamma^{1/(1-\gamma)}(1−1/n)n=γ1/(1−γ)。因为
limn→∞(1−1n)n=exp(−1)≈0.3679,\lim_{n \rightarrow \infty} \left(1-\frac{1}{n}\right)^n = \exp(-1) \approx 0.3679,n→∞lim(1−n1)n=exp(−1)≈0.3679,
所以当γ→1\gamma \rightarrow 1γ→1时,γ1/(1−γ)=exp(−1)\gamma^{1/(1-\gamma)}=\exp(-1)γ1/(1−γ)=exp(−1),如0.9520≈exp(−1)0.95^{20} \approx \exp(-1)0.9520≈exp(−1)。如果把exp(−1)\exp(-1)exp(−1)当作一个比较小的数,我们可以在近似中忽略所有含γ1/(1−γ)\gamma^{1/(1-\gamma)}γ1/(1−γ)和比γ1/(1−γ)\gamma^{1/(1-\gamma)}γ1/(1−γ)更高阶的系数的项。例如,当γ=0.95\gamma=0.95γ=0.95时,
yt≈0.05∑i=0190.95ixt−i.y_t \approx 0.05 \sum_{i=0}^{19} 0.95^i x_{t-i}.yt≈0.05i=0∑190.95ixt−i.
因此,在实际中,我们常常将yty_tyt看作是对最近1/(1−γ)1/(1-\gamma)1/(1−γ)个时间步的xtx_txt值的加权平均。例如,
- 当γ=0.95\gamma = 0.95γ=0.95时,yty_tyt可以被看作对最近20个时间步的xtx_txt值的加权平均
- 当γ=0.9\gamma = 0.9γ=0.9时,yty_tyt可以看作是对最近10个时间步的xtx_txt值的加权平均
- 而且,离当前时间步ttt越近的xtx_txt值获得的权重越大(越接近1)
由指数加权移动平均理解动量法
现在,我们对动量法的速度变量做变形:
vt←γvt−1+(1−γ)(ηt1−γgt).\boldsymbol{v}_t \leftarrow \gamma \boldsymbol{v}{t-1} + (1 - \gamma) \left(\frac{\eta_t}{1 - \gamma} \boldsymbol{g}_t\right). vt←γvt−1+(1−γ)(1−γηtgt).
由指数加权移动平均的形式可得,速度变量vt\boldsymbol{v}_tvt实际上对序列{ηt−igt−i/(1−γ):i=0,…,1/(1−γ)−1}\{{\eta_{t-i}\boldsymbol{g}_{t-i} /(1-\gamma):i=0,\ldots,1/(1-\gamma)-1}\}{ηt−igt−i/(1−γ):i=0,…,1/(1−γ)−1}做了指数加权移动平均。
- 换句话说,相比于小批量随机梯度下降,动量法在每个时间步的自变量更新量近似于将最近1/(1−γ)1/(1-\gamma)1/(1−γ)个时间步的普通更新量(即学习率乘以梯度)做了指数加权移动平均后再除以1−γ1-\gamma1−γ
所以,在动量法中,自变量在各个方向上的移动幅度不仅取决当前梯度,还取决于过去的各个梯度在各个方向上是否一致。
之前的优化问题中,所有梯度在水平方向上为正(向右),而在竖直方向上时正(向上)时负(向下)。这样,我们就可以使用较大的学习率,从而使自变量向最优解更快移动。
实现动量法
相对于小批量随机梯度下降,动量法需要对每一个自变量维护一个同它一样形状的速度变量,且超参数里多了动量超参数。实现中,将速度变量用更广义的状态变量states表示。
def get_data_ch7(): data = np.genfromtxt('../../data/airfoil_self_noise.dat', delimiter='\t')data = (data - data.mean(axis=0)) / data.std(axis=0)return torch.tensor(data[:1500, :-1], dtype=torch.float32), \torch.tensor(data[:1500, -1], dtype=torch.float32) # 前1500个样本(每个样本5个特征)def train_ch7(optimizer_fn, states, hyperparams, features, labels,batch_size=10, num_epochs=2):# 初始化模型net, loss = linreg, squared_lossw = torch.nn.Parameter(torch.tensor(np.random.normal(0, 0.01, size=(features.shape[1], 1)), dtype=torch.float32),requires_grad=True)b = torch.nn.Parameter(torch.zeros(1, dtype=torch.float32), requires_grad=True)def eval_loss():return loss(net(features, w, b), labels).mean().item()ls = [eval_loss()]data_iter = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(features, labels), batch_size, shuffle=True)
features, labels = get_data_ch7()def init_momentum_states():v_w = torch.zeros((features.shape[1], 1), dtype=torch.float32)v_b = torch.zeros(1, dtype=torch.float32)return (v_w, v_b)def sgd_momentum(params, states, hyperparams):for p, v in zip(params, states):v.data = hyperparams['momentum'] * v.data + hyperparams['lr'] * p.grad.datap.data -= v.data
先将动量超参数momentum设0.5,这时可以看成是特殊的小批量随机梯度下降:
- 其小批量随机梯度为最近2个时间步的2倍小批量梯度的加权和。
train_ch7(sgd_momentum, init_momentum_states(),{'lr': 0.02, 'momentum': 0.5}, features, labels)
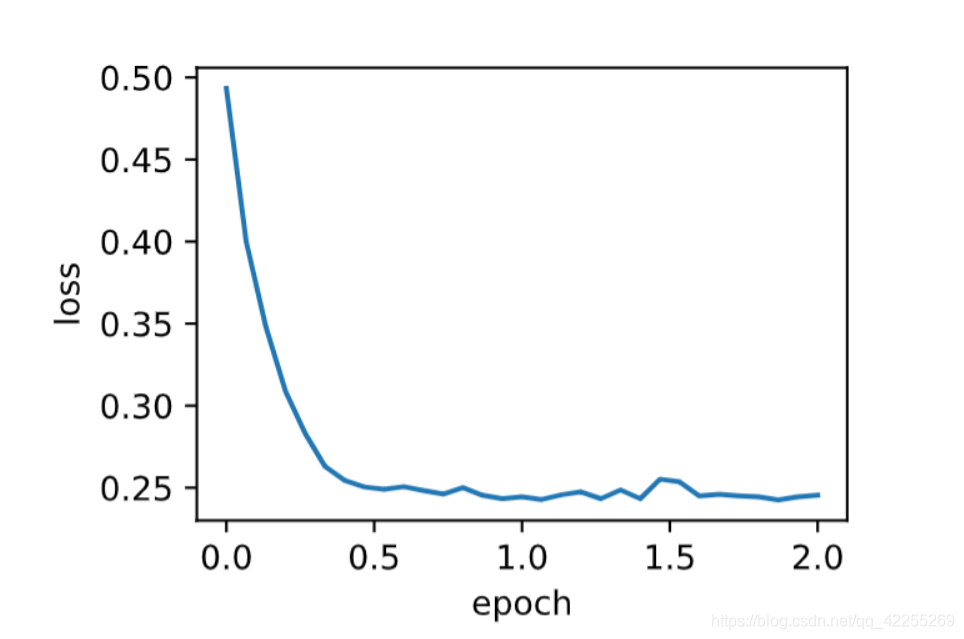
将动量超参数momentum增大到0.9,这时依然可以看成是特殊的小批量随机梯度下降:
- 其小批量随机梯度为最近10个时间步的10倍小批量梯度的加权和。我们先保持学习率0.02不变
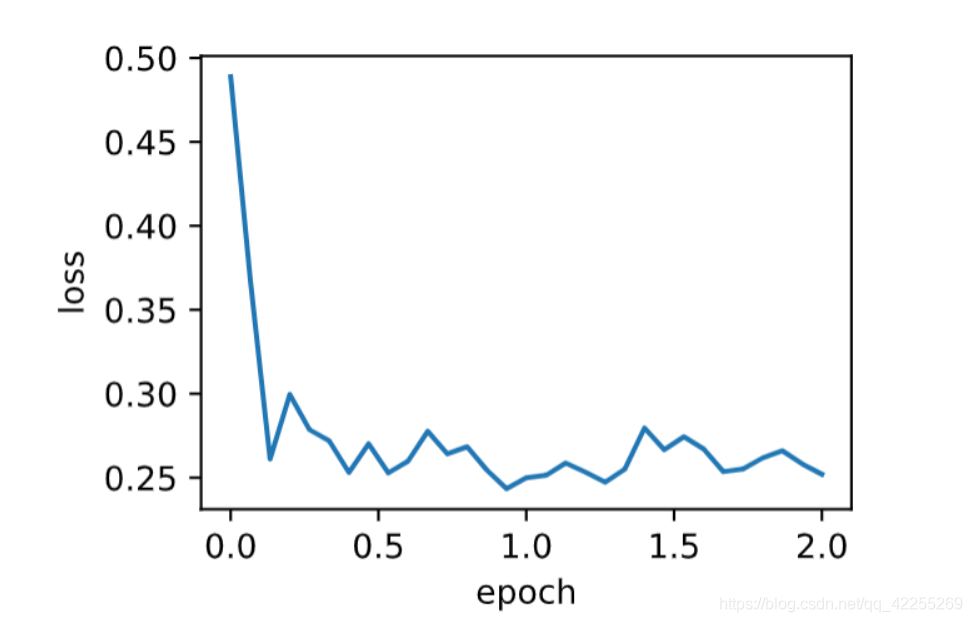
目标函数值在后期迭代过程中的变化不够平滑。直觉上,10倍小批量梯度比2倍小批量梯度大了5倍,试着将学习率减小到原来的1/5。此时目标函数值在下降了一段时间后变化更加平滑。
train_ch7(sgd_momentum, init_momentum_states(),{'lr': 0.004, 'momentum': 0.9}, features, labels)
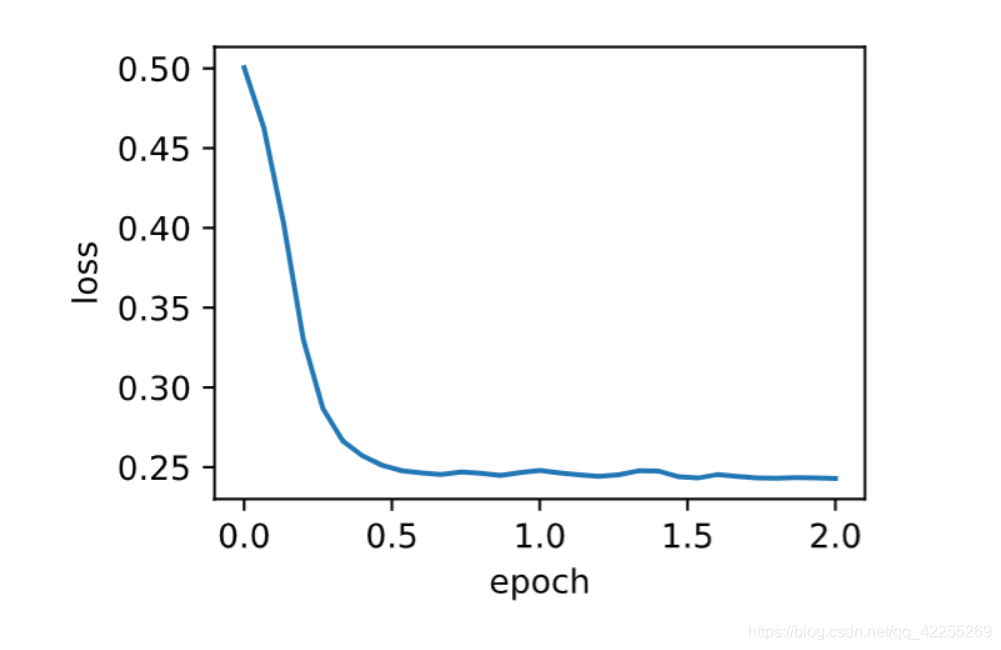
- 动量法使用了指数加权移动平均的思想。它将过去时间步的梯度做了加权平均,且权重按时间步指数衰减。
- 动量法使得相邻时间步的自变量更新在方向上更加一致。









)








)
