双向循环神经网络
一般,我们认为循环神经网络模型都是假设当前时间步是由前面的较早时间步的序列决定的,因此它们都将信息通过隐藏状态从前往后传递。
有时候,当前时间步也可能由后面时间步决定。
例如,当我们写下一个句子时,可能会根据句子后面的词来修改句子前面的用词。双向循环神经网络通过增加从后往前传递信息的隐藏层来更灵活地处理这类信息。
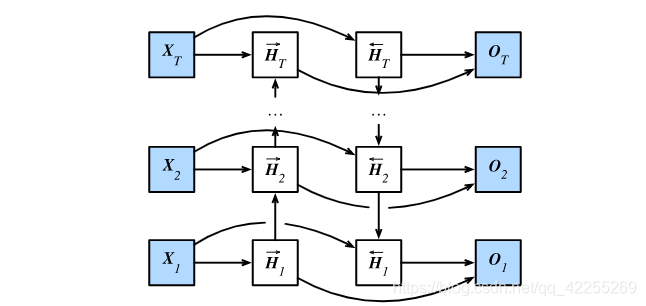
- 给定时间步ttt的小批量输入Xt∈Rn×d\boldsymbol{X}_t \in \mathbb{R}^{n \times d}Xt∈Rn×d(样本数为nnn,输入个数为ddd)
- 隐藏层激活函数为ϕ\phiϕ。
在双向循环神经网络的架构中, 设
- 该时间步正向隐藏状态为H→t∈Rn×h\overrightarrow{\boldsymbol{H}}_t \in \mathbb{R}^{n \times h}Ht∈Rn×h(正向隐藏单元个数为hhh)
- 反向隐藏状态为H←t∈Rn×h\overleftarrow{\boldsymbol{H}}_t \in \mathbb{R}^{n \times h}Ht∈Rn×h(反向隐藏单元个数为hhh)。
我们可以分别计算正向隐藏状态和反向隐藏状态:
H→t=ϕ(XtWxh(f)+H→t−1Whh(f)+bh(f)),H←t=ϕ(XtWxh(b)+H←t+1Whh(b)+bh(b))\begin{aligned} \overrightarrow{\boldsymbol{H}}_t &= \phi(\boldsymbol{X}_t \boldsymbol{W}_{xh}^{(f)} + \overrightarrow{\boldsymbol{H}}_{t-1} \boldsymbol{W}_{hh}^{(f)} + \boldsymbol{b}_h^{(f)}),\\ \overleftarrow{\boldsymbol{H}}_t &= \phi(\boldsymbol{X}_t \boldsymbol{W}_{xh}^{(b)} + \overleftarrow{\boldsymbol{H}}_{t+1} \boldsymbol{W}_{hh}^{(b)} + \boldsymbol{b}_h^{(b)})\end{aligned} HtHt=ϕ(XtWxh(f)+Ht−1Whh(f)+bh(f)),=ϕ(XtWxh(b)+Ht+1Whh(b)+bh(b))
其中权重Wxh(f)∈Rd×h\boldsymbol{W}_{xh}^{(f)} \in \mathbb{R}^{d \times h}Wxh(f)∈Rd×h、Whh(f)∈Rh×h\boldsymbol{W}_{hh}^{(f)} \in \mathbb{R}^{h \times h}Whh(f)∈Rh×h、Wxh(b)∈Rd×h\boldsymbol{W}_{xh}^{(b)} \in \mathbb{R}^{d \times h}Wxh(b)∈Rd×h、Whh(b)∈Rh×h\boldsymbol{W}_{hh}^{(b)} \in \mathbb{R}^{h \times h}Whh(b)∈Rh×h和偏差 bh(f)∈R1×h\boldsymbol{b}_h^{(f)} \in \mathbb{R}^{1 \times h}bh(f)∈R1×h、bh(b)∈R1×h\boldsymbol{b}_h^{(b)} \in \mathbb{R}^{1 \times h}bh(b)∈R1×h均为模型参数。
然后通过连结两个方向的隐藏状态H→t\overrightarrow{\boldsymbol{H}}_tHt和H←t\overleftarrow{\boldsymbol{H}}_tHt来得到隐藏状态Ht∈Rn×2h\boldsymbol{H}_t \in \mathbb{R}^{n \times 2h}Ht∈Rn×2h,并将其输入到输出层。
输出层计算输出Ot∈Rn×q\boldsymbol{O}_t \in \mathbb{R}^{n \times q}Ot∈Rn×q(输出个数为qqq):
Ot=HtWhq+bq,\boldsymbol{O}_t = \boldsymbol{H}_t \boldsymbol{W}_{hq} + \boldsymbol{b}_q,Ot=HtWhq+bq,
其中权重Whq∈R2h×q\boldsymbol{W}_{hq} \in \mathbb{R}^{2h \times q}Whq∈R2h×q和偏差bq∈R1×q\boldsymbol{b}_q \in \mathbb{R}^{1 \times q}bq∈R1×q为输出层的模型参数。不同方向上的隐藏单元个数也可以不同。












)






