PyTorch框架学习十——基础网络层(卷积、转置卷积、池化、反池化、线性、激活函数)
- 一、卷积层
- 二、转置卷积层
- 三、池化层
- 1.最大池化nn.MaxPool2d
- 2.平均池化nn.AvgPool2d
- 四、反池化层
- 最大值反池化nn.MaxUnpool2d
- 五、线性层
- 六、激活函数层
- 1.nn.Sigmoid
- 2.nn.Tanh
- 3.nn.ReLU
- 4.nn.LeakyReLU、nn.PReLU、nn.RReLU
- (1)nn.LeakyReLU
- (2)nn.PReLU
- (3)nn.RReLU
上次笔记介绍了PyTorch中如何进行网络搭建,是从宏观上来学习,这次笔记介绍一个网络内部的具体网络层,从微观拆解。
一、卷积层
因为对卷积运算有基础,就不从0开始写了,下面概括地介绍相关概念后,重点放在卷积层在PyTorch的实现上。
卷积运算:卷积核在输入信号(图像)上滑动,相应位置上进行乘加。网上有很多图例,清晰地介绍了卷积运算的过程,这里不赘述。
卷积核:又称为滤波器、过滤器,可以认为是某种模式或特征。
卷积维度:一般,卷积核在几个维度上滑动,就是几维卷积,如下图所示:
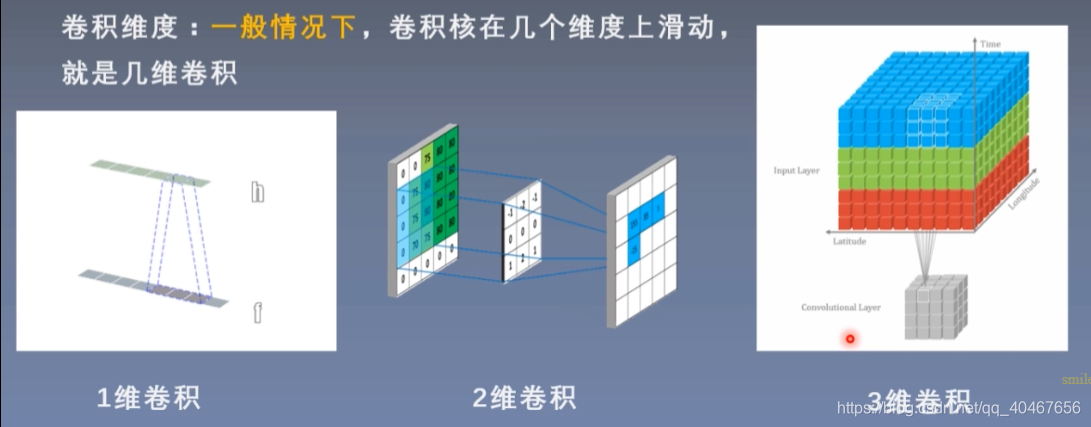
上图有个小问题,没有考虑通道数,图中所示的都是一个通道的情况,比如二维灰度图像,通道数为1,如果是三通道的RGB二维图像呢?那卷积核也会变成3通道,每个通道进行乘加之后得到的结果再相加,才是最后的卷积结果。
PyTorch上的实现:
torch.nn.Conv2d(in_channels: int, out_channels: int, kernel_size: Union[int, Tuple[int, int]], stride: Union[int, Tuple[int, int]] = 1, padding: Union[int, Tuple[int, int]] = 0, dilation: Union[int, Tuple[int, int]] = 1, groups: int = 1, bias: bool = True, padding_mode: str = 'zeros')
参数如下图所示:

- in_channels:输入图像的通道数,也决定了卷积核的通道数。
- out_channels:输出图像的通道数,等于卷积核的个数。
- kernel_size:卷积核的尺寸。
- stride:卷积核滑动步长,默认为1。
- padding:填充像素的个数,默认为0。
- padding_mode:填充模式,有四种:‘zeros’、‘reflect’、‘replicate’、‘circular’,默认为‘zeros’。
- dilation:空洞卷积大小,即卷积核元素间距,默认为1。
- groups:分组卷积设置,默认为1,即不分组。
- bias:偏置,默认为True。
有一个需要注意的地方:

就是说,kernel_size,stride,padding和dilation四个参数,如果是一个值(int类),则对H和W两个维度都是这个值;如果是两个int组成的元组,则第一个数对应H维度,第二个数对应W维度,下面举几个例子:
>>> m = nn.Conv2d(16, 33, 3, stride=2)
这里kernel_size等于一个值3,即H维和W维的尺寸都是3,等价于(3, 3);stride等于一个值2,即滑动时在H和W两个维度上步长都是2。
>>> m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2))
而这个卷积层,kernel_size为(3, 5),即H维是3,W维是5,即代表大小为3×5的卷积核;步长为(2, 1),即H维上滑动步长为2,W维上滑动步长为1;padding为(4, 2),即H维(上下各)填充4个像素,W维(左右各)填充2个像素。
还有一个需要注意的地方:输入输出图像尺寸的关系,这个对于分析非常重要。
如果不考虑padding和dilation这两个的影响,那么输出图像的尺寸等于:

如果全都考虑的话,就等于:

最后用一个例子来形象地体现卷积层的作用:
# load img
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png")
img = Image.open(path_img).convert('RGB') # 0~255# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0) # C*H*W to B*C*H*W# create convolution layer
conv_layer = nn.Conv2d(3, 1, 3) # input:(i, o, size) weights:(o, i , h, w)
nn.init.xavier_normal_(conv_layer.weight.data)# calculation
img_conv = conv_layer(img_tensor)
构建了一个3×3×3的卷积核来对图像lena.png进行卷积,将卷积结果可视化如下:
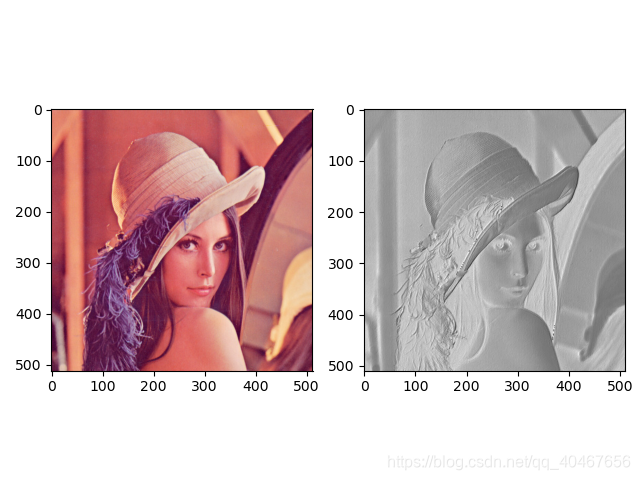
左边是原图,右边是卷积之后的结果,查看两图的尺寸:
卷积前尺寸:torch.Size([1, 3, 512, 512])
卷积后尺寸:torch.Size([1, 1, 510, 510])
卷积后的结果,其实就是某一种模式或者说是特征图,这是该卷积核卷积之后的结果,我们将卷积核内的权重换一下,就可以得到另一种不同的特征图:
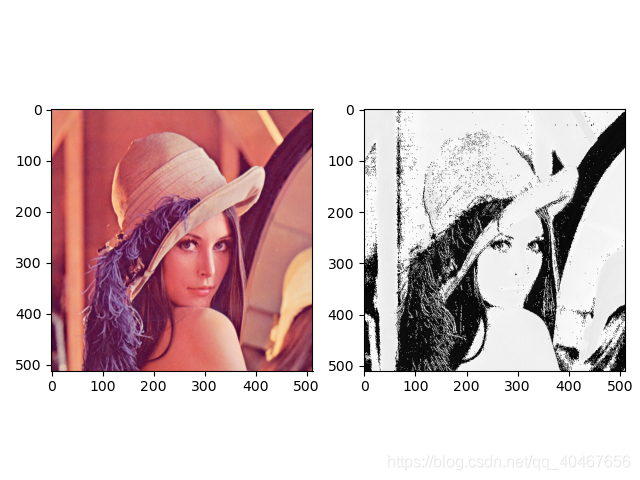

所以用多个卷积核就可以得到多个特征图。
二、转置卷积层
用于对图像进行上采样Upsample,即可以将小尺寸的图像转置卷积为大尺寸。
因为卷积操作是通过矩阵相乘实现的,而转置卷积之所以得名,就是它的卷积核的尺寸与相应的卷积操作的卷积核的尺寸是一个转置的关系,只是尺寸有转置的关系,元素是不相同的,转置卷积也无法恢复到原始图像了。
PyTorch中转置卷积的实现:
torch.nn.ConvTranspose2d(in_channels: int, out_channels: int, kernel_size: Union[int, Tuple[int, int]], stride: Union[int, Tuple[int, int]] = 1, padding: Union[int, Tuple[int, int]] = 0, output_padding: Union[int, Tuple[int, int]] = 0, groups: int = 1, bias: bool = True, dilation: int = 1, padding_mode: str = 'zeros')
参数如下所示:

它的输入输出尺寸的关系与卷积层正好相反:

最后来看一个转置卷积的例子(输入图像还是卷积时用的lena.png):
conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2) # input:(i, o, size)
nn.init.xavier_normal_(conv_layer.weight.data)# calculation
img_conv = conv_layer(img_tensor)
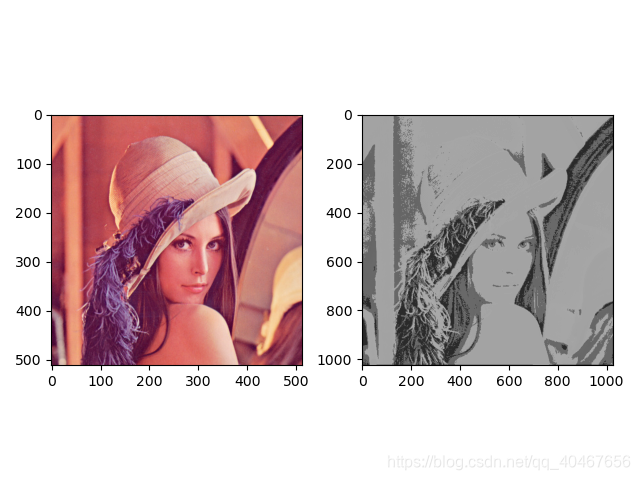
可以得到尺寸更大的特征图,在图像分割时经常用到,看一下两图的尺寸:
卷积前尺寸:torch.Size([1, 3, 512, 512])
卷积后尺寸:torch.Size([1, 1, 1025, 1025])
三、池化层
池化运算:对信号进行“收集”并“总结”,类似水池收集水资源,因而得名池化层。
“收集”:像素个数由多变少,“总结”:最大值池化/平均值池化。
具体池化操作不再赘述,给一张最大值池化和平均值池化的图:
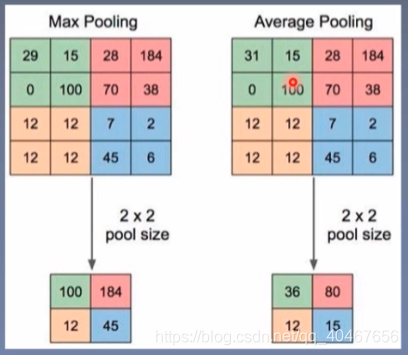
主要看一下PyTorch中池化层的实现:
1.最大池化nn.MaxPool2d
功能:对二维图像进行最大值池化。
torch.nn.MaxPool2d(kernel_size: Union[int, Tuple[int, ...]], stride: Union[int, Tuple[int, ...], None] = None, padding: Union[int, Tuple[int, ...]] = 0, dilation: Union[int, Tuple[int, ...]] = 1, return_indices: bool = False, ceil_mode: bool = False)
参数如下所示:

- kernel_size:池化核尺寸。
- stride:滑动尺寸,默认值为kernel_size。
- padding:填充像素的个数。
- dilation:池化核内元素间隔步长。
- return_indices:记录池化像素的索引,反池化的时候用到。
- ceil_mode:如果为True,输出尺寸向上取整,否则向下取整(默认)。
池化前后的图像尺寸关系如下:

若不考虑padding、dilation,且默认状态下 kernel_size = stride 则简化版公式为:

最后看一个例子:
maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2)) # input:(i, o, size) weights:(o, i , h, w)
img_pool = maxpool_layer(img_tensor)
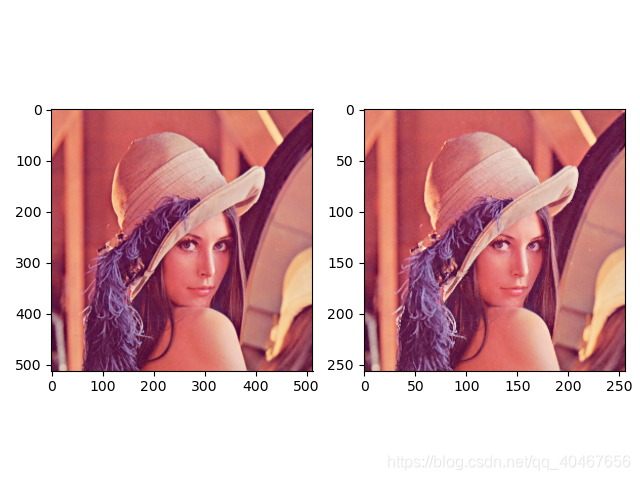
看起来好像差不多,但是很明显池化后图片质量下降了一点,毕竟池化是一个抽象特征的过程,看一下池化前后尺寸:
池化前尺寸:torch.Size([1, 3, 512, 512])
池化后尺寸:torch.Size([1, 3, 256, 256])
尺寸变成原来的一半。
2.平均池化nn.AvgPool2d
功能:对二维图像进行平均值池化。
torch.nn.AvgPool2d(kernel_size: Union[int, Tuple[int, int]], stride: Union[int, Tuple[int, int], None] = None, padding: Union[int, Tuple[int, int]] = 0, ceil_mode: bool = False, count_include_pad: bool = True, divisor_override: bool = None)
参数如下所示:
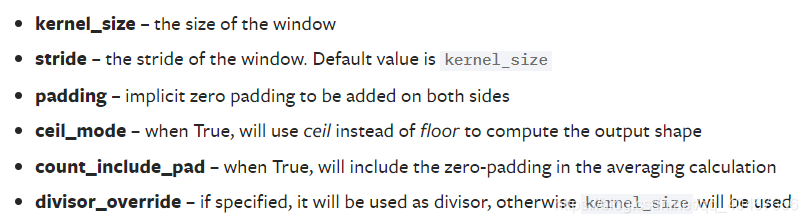
- 前四个参数与最大池化一样。
- count_include_pad:若为True,平均池化计算时会包括填充值0。
- divisor_override:除法因子,平均池化计算时默认是除以kernel_size的,如2×2的池化核,平均计算时就是除以(2×2 =)4,而若设置了除法因子,则除以除法因子。
平均池化前后图像的尺寸计算公式如下:

若不考虑padding,默认情况下kernel_size=stride,则简化计算公式与最大池化一样:

看两个例子:
avgpoollayer = nn.AvgPool2d((2, 2), stride=(2, 2)) # input:(i, o, size) weights:(o, i , h, w)
img_pool = avgpoollayer(img_tensor)
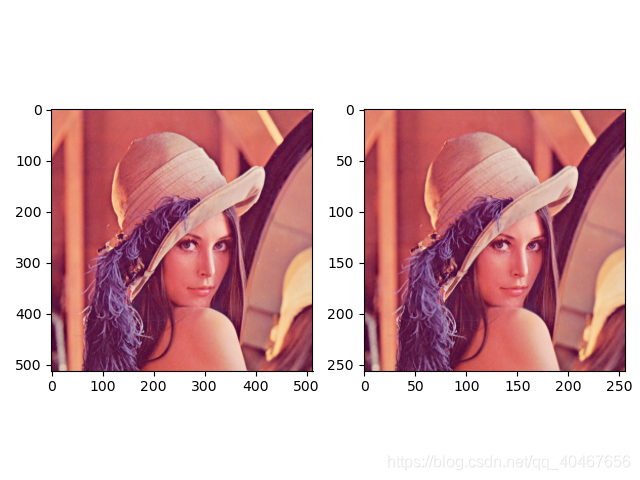
和最大值池化类似,看起来差不多,但是质量上下降了一点;而且与最大值池化相比,平均池化后的图偏暗一点,因为最大值池化取得像素都是最大值,而平均值池化是取得平均,像素值要普遍小于最大值,所以偏暗。
第二个例子着重关注除法因子:
img_tensor = torch.ones((1, 1, 4, 4))
avgpool_layer = nn.AvgPool2d((2, 2), stride=(2, 2), divisor_override=3)
img_pool = avgpool_layer(img_tensor)print("raw_img:\n{}\npooling_img:\n{}".format(img_tensor, img_pool))
输出为:
raw_img:
tensor([[[[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.]]]])
pooling_img:
tensor([[[[1.3333, 1.3333],[1.3333, 1.3333]]]])
如果不设置除法因子,应该平均计算的时候是除以4,得到的结果全为1,而设置除法因子之后就不除以4而是除以除法因子3,所以得到4/3=1.3333。
四、反池化层
是池化的一个“逆”过程,但这个“逆”只是通过上采样将尺寸恢复到原来,像素值是不能恢复成原来一模一样的,因为像最大池化,除最大值之外的像素都已经丢弃了。所以严格来说池化是不可逆的,反池化只是“近似”逆过程。
最大值反池化nn.MaxUnpool2d
功能:对二维图像进行最大值池化上采样。
torch.nn.MaxUnpool2d(kernel_size: Union[int, Tuple[int, int]], stride: Union[int, Tuple[int, int], None] = None, padding: Union[int, Tuple[int, int]] = 0)
参数如下所示:

它是依据最大值池化层的输出以及最大值的索引来恢复原图像,非最大值的地方全都设置为0。
看一个例子:
# pooling
img_tensor = torch.randint(high=5, size=(1, 1, 4, 4), dtype=torch.float)
maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2), return_indices=True)
img_pool, indices = maxpool_layer(img_tensor)# unpooling
# img_reconstruct = torch.randn_like(img_pool, dtype=torch.float)
maxunpool_layer = nn.MaxUnpool2d((2, 2), stride=(2, 2))
img_unpool = maxunpool_layer(img_pool, indices)print("raw_img:\n{}\nimg_pool:\n{}".format(img_tensor, img_pool))
print("img_pool:\n{}\nimg_unpool:\n{}".format(img_pool, img_unpool))
输出结果为:
raw_img:
tensor([[[[0., 4., 4., 3.],[3., 3., 1., 1.],[4., 2., 3., 4.],[1., 3., 3., 0.]]]])
img_pool:
tensor([[[[4., 4.],[4., 4.]]]])
img_pool:
tensor([[[[4., 4.],[4., 4.]]]])
img_unpool:
tensor([[[[0., 4., 4., 0.],[0., 0., 0., 0.],[4., 0., 0., 4.],[0., 0., 0., 0.]]]])
当然你可以用得到的索引去unpool其他的数据,如下所示:
# pooling
img_tensor = torch.randint(high=5, size=(1, 1, 4, 4), dtype=torch.float)
maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2), return_indices=True)
img_pool, indices = maxpool_layer(img_tensor)# unpooling
img_reconstruct = torch.randn_like(img_pool, dtype=torch.float)
maxunpool_layer = nn.MaxUnpool2d((2, 2), stride=(2, 2))
img_unpool = maxunpool_layer(img_reconstruct, indices)print("raw_img:\n{}\nimg_pool:\n{}".format(img_tensor, img_pool))
print("img_reconstruct:\n{}\nimg_unpool:\n{}".format(img_reconstruct, img_unpool))
raw_img:
tensor([[[[0., 4., 4., 3.],[3., 3., 1., 1.],[4., 2., 3., 4.],[1., 3., 3., 0.]]]])
img_pool:
tensor([[[[4., 4.],[4., 4.]]]])
img_reconstruct:
tensor([[[[-1.0276, -0.5631],[-0.8923, -0.0583]]]])
img_unpool:
tensor([[[[ 0.0000, -1.0276, -0.5631, 0.0000],[ 0.0000, 0.0000, 0.0000, 0.0000],[-0.8923, 0.0000, 0.0000, -0.0583],[ 0.0000, 0.0000, 0.0000, 0.0000]]]])
这个演示的目的就更接近真实情况,因为池化之后是不会立即反池化的,还会经过一些其他的网络层计算,从而原来的像素值已经发生了变化,接下来的反池化就是要将已经变化的数据上采样到原来的尺寸,像素值肯定不再是原来的了。
平均池化的反池化PyTorch中没有,估计是无法反池化。
五、线性层
线性层又称为全连接层,其每个神经元与上一层所有神经元相连。实现对前一层的线性组合,线性变换。
PyTorch中线性层的实现是nn.Linear:
torch.nn.Linear(in_features: int, out_features: int, bias: bool = True)
所做的操作:

参数如下所示:

- in_features:输入结点数。
- out_features:输出结点数。
- bias:若设置为False,将不加上bias,默认为True。
下面看一个例子,构建一个3×4的线性层:
inputs = torch.tensor([[1., 2, 3]])
linear_layer = nn.Linear(3, 4)
linear_layer.weight.data = torch.tensor([[1., 1., 1.],[2., 2., 2.],[3., 3., 3.],[4., 4., 4.]])
linear_layer.bias.data.fill_(0.5)
output = linear_layer(inputs)
print(inputs, inputs.shape)
print(linear_layer.weight.data, linear_layer.weight.data.shape)
print(output, output.shape)
tensor([[1., 2., 3.]]) torch.Size([1, 3])
tensor([[1., 1., 1.],[2., 2., 2.],[3., 3., 3.],[4., 4., 4.]]) torch.Size([4, 3])
tensor([[ 6.5000, 12.5000, 18.5000, 24.5000]], grad_fn=<AddmmBackward>) torch.Size([1, 4])
六、激活函数层
激活函数对特征进行非线性变换,赋予多层神经网络有深度的意义,如果没有非线性变换,多少层网络层都可以等效为一层。
下面介绍几个常用的激活函数:
1.nn.Sigmoid
计算公式:

该函数图像及其导数如下所示:
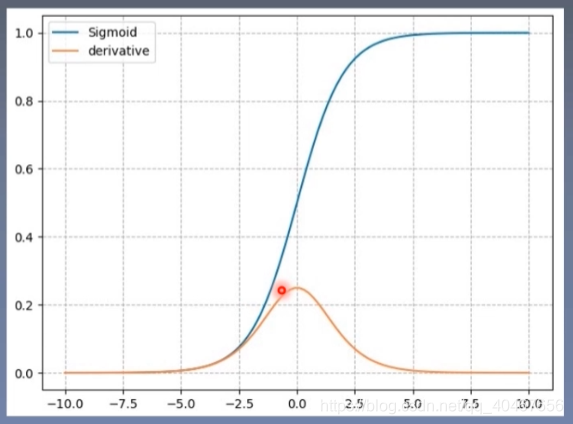
特点:
- 输出在(0,1)之间,符合概率的意义;
- 导数范围[0, 0.25],非常小,在不断地导数迭代中容易导致梯度消失;
- 输出的均值非零,破坏了数据分布。
注意维度:

用法如下:
>>> m = nn.Sigmoid()
>>> input = torch.randn(2)
>>> output = m(input)
2.nn.Tanh
计算公式:

该函数及其导数如下图所示:
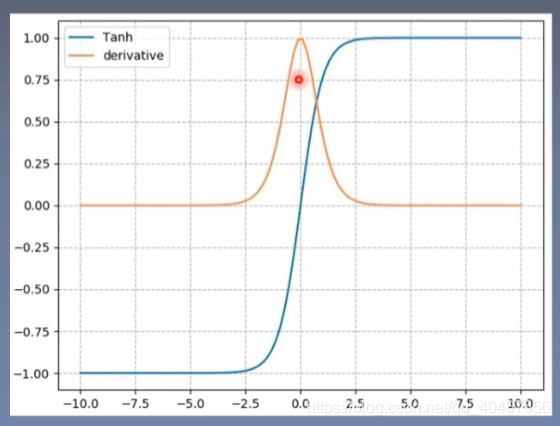
特点:
- 输出值在(-1, 1),输出数据符合0均值。
- 导数范围是(0,1),如今网络层数很深,也容易导致梯度消失。
用法如下:
>>> m = nn.Tanh()
>>> input = torch.randn(2)
>>> output = m(input)
3.nn.ReLU
计算公式:

该函数及其导数如下图所示:
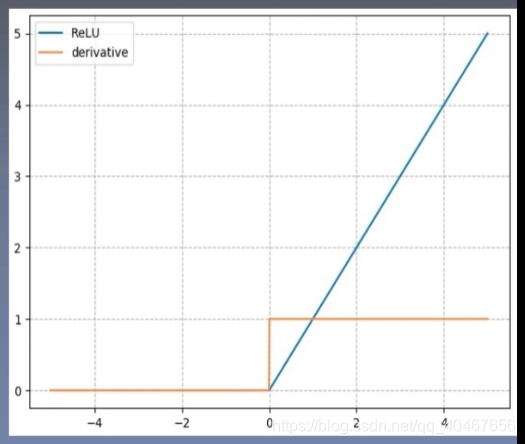
特点:
- 输出值均为正数,负半轴导致死神经元。
- 导数为1,缓解梯度消失,但容易引发梯度爆炸。
4.nn.LeakyReLU、nn.PReLU、nn.RReLU
针对上述ReLU负半轴为0导致死神经元的问题,提出了一些解决方案,下面介绍其中三种常用的:
(1)nn.LeakyReLU
给负半轴一个很小的固定斜率。
torch.nn.LeakyReLU(negative_slope: float = 0.01, inplace: bool = False)
计算公式:

参数:
- negative_slope:负半轴的斜率,默认为0.01。
- inplace:略。
(2)nn.PReLU
负半轴斜率不再人为固定,而是可学习的。
torch.nn.PReLU(num_parameters: int = 1, init: float = 0.25)
计算公式:

参数:

- num_parameters:可学习参数a(斜率)的数目,只能为1或者等于输入图像的通道数,默认为1。
- init:a(斜率)的初始值,默认为0.25,在网络迭代过程中会更新。
(3)nn.RReLU
斜率从均匀分布中随机采样。
torch.nn.RReLU(lower: float = 0.125, upper: float = 0.3333333333333333, inplace: bool = False)

参数:

- lower:均匀分布下限。
- upper:均匀分布上限。
- inplace:略。
下图展示了三种ReLU的图像:
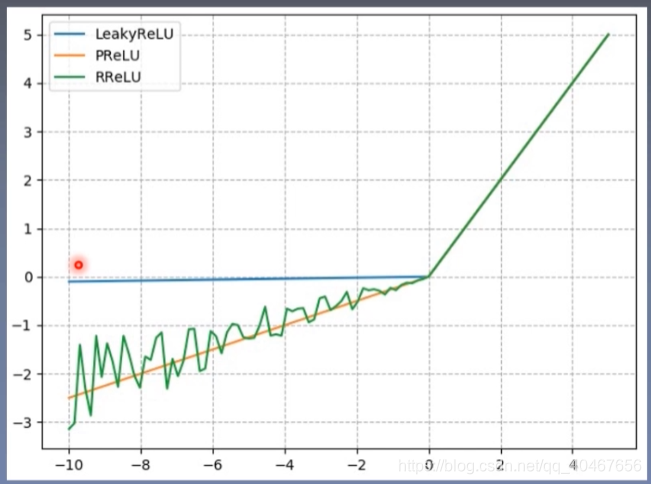





类型转换函数)













)