• 序列数据建模
  • 输入序列–>输出序列
  • 预测序列的下一项（监督）
    • 模糊了监督和非监督
• 有的cnn对序列不适用：
  • cnn假设：离得远的关系远，有关系的都在附近
  • 序列：可能长距离也有相关的（一段文字的代词）
    RNN结构
• RNN
  • 结构：
    • 层间全连接
    • 层内全连接?
    • 自连接
  • 功能强大
    • 计算力够且单元数够的情况下
  • 每个时间点的输入输出不同–
    • 参数共享：一个序列的从前到后逐个输入到网络中（矩阵）（每个时间点不同的字进的都是同一个神经元–参数一样的）
    • 矩阵：行（时间，一行一个字的表达），列（神经元数目）
  • 特点（展开后的（可认为是：
    • 权值约束（共享
    • 多层
    • 前向网络
  • 损失函数：
    • 平方损失
    • 交叉熵
  • 训练：采用权值一致的BP算法（更新也一致
    • BP容易实现权值的线性约束
      • $约束w^1=w^2,令\Delta w^1=\Delta w^2=\frac{\partial E}{\partial w^1}+\frac{\partial E}{\partial w^2}$
    • BPTT(时间域上的BP
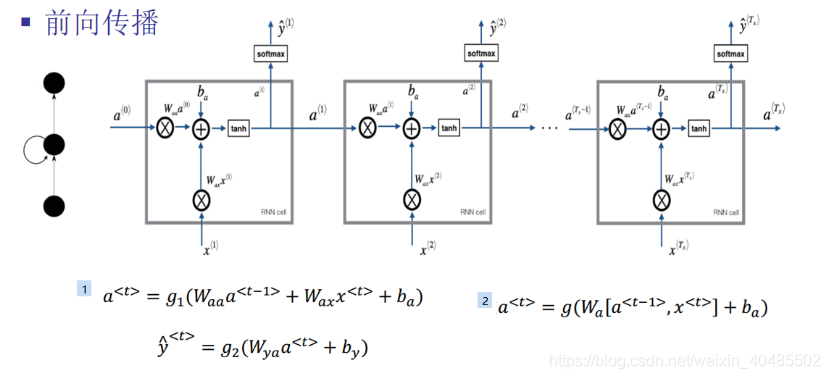
      1. 前向
         • 输入层：（常用tanh$a^t=g_1(W_{aa}{a}^{t-1}+W_{ax}{x}^t+b_a)=g_1(W_a[a^{t-1},x^t]+b_a),z_a^t=W_{aa}{a}^{t-1}+W_{ax}{x}^t+b_a$
         • 输出层：（softmax${\hat{y}}^t=g_2(W_{ya}{a}^t+b_y),z_y^t=W_{ya}{a}^t+b_y$
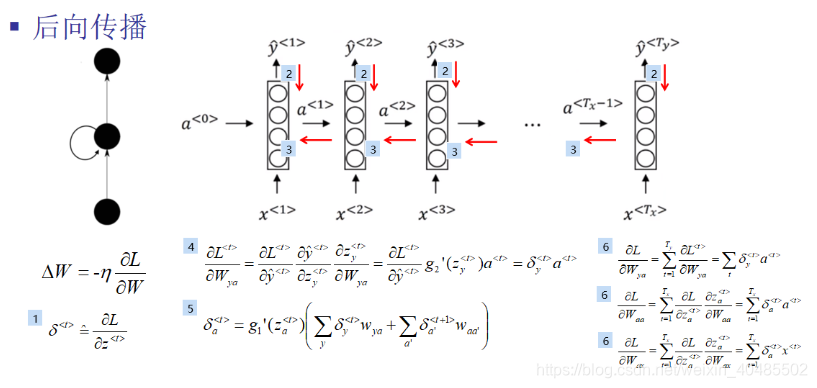
      2. 计算每一个时间的链式导数$\frac{\partial E}{\partial w^i}$
         • $\Delta W=-\eta \frac{\partial L}{\partial W},\eta 学习率$
         • ${\delta }^t=\frac{\partial L}{\partial z^t}$
         • $\frac{\partial L^t}{\partial W_{y}a}=\frac{\partial L^t}{\partial {\hat{y}}^t}\frac{\partial {\hat{y}}^t}{\partial z_y^t}\frac{\partial z_y^t}{\partial W_{y}a}=\frac{\partial L^t}{\partial {\hat{y}}^t}{g}_2^{\prime }(z_y^t)a^t={\delta }_y^t{a}^t$
         • ${\delta }_a^t=g_1^{\prime }(z_a^t)(W_{ya}^T{\delta }_y^t+W_{a{a}^{\prime }}^T{\delta }_{a^{\prime }}^{t+1})$
           • 前一项：$W_{ya}^T{\delta }_y^t:当前层的y传来的$
           • 后一项：$W_{a{a}^{\prime }}^T{\delta }_{a^{\prime }}^{t+1}:其他隐层（上一时刻的）传递而来的$
      3. 将所有时间的导数加在一起$约束w^1=w^2,令\Delta w^1=\Delta w^2=\frac{\partial E}{\partial w^1}+\frac{\partial E}{\partial w^2}$
         • $\frac{\partial L^t}{\partial W_{y}a}={\Sigma }_{t=1}^{T_y}{\delta }_y^t{a}^t$
         • $\frac{\partial L^t}{\partial W_{a}a}={\Sigma }_{t=1}^{T_x}{\delta }_a^t{a}^t$
         • $\frac{\partial L^t}{\partial W_{y}a}={\Sigma }_{t=1}^{T_x}{\delta }_a^t{x}^t$
         • 这里的x、y、W都是向量、矩阵，可以视作一个向量中一个元素一个神经元
    • 交叉熵loss：
      • $L^t({\hat{y}}^t,y^t)=-y^{t}log({\hat{y}}^t)-(1-y^t)log(1-{\hat{y}}^t)$
      • $用这个损失函数：L(\hat{y},y)={\Sigma }_{t=1}^{T_y}{L}^t({\hat{y}}^t,y^t)$
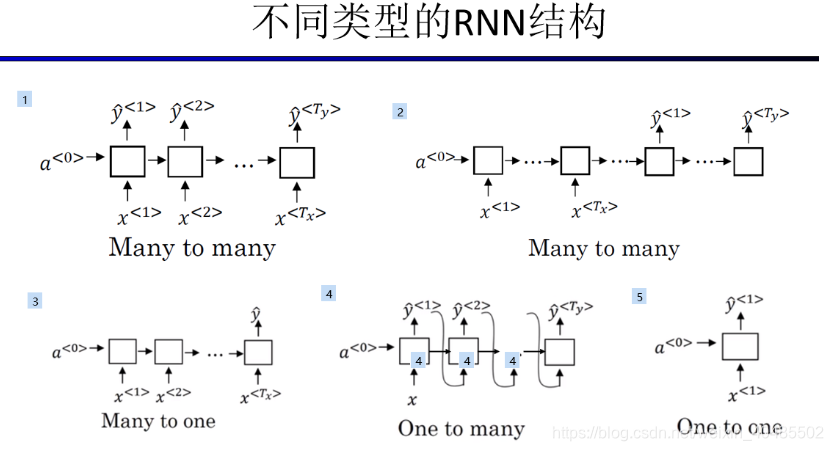
  • 结构
    • 多对多1
    • 多对多2（encoder+decoder）
      • 机器翻译
    • 多对1
      • 情感分析
    • 1对多
    • 一对一
• 语言模型（多对多1）
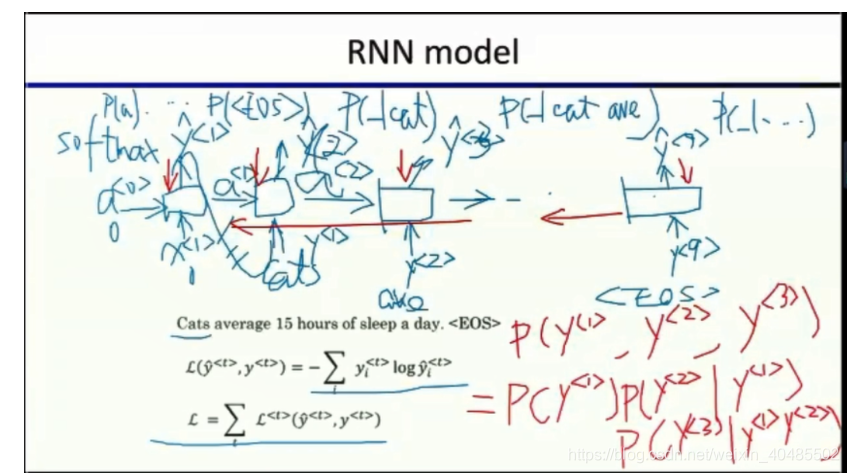
  • 计算P(sentence)，大的好=$P(y^1,y^2,...,y^n)=P(cats在开头)P(average|cats)P(15|average,cats)$
    • RNN的每个时刻的输出y^1==第一个单词在开头的概率$P(cats在开头)$
    • 第二个词的输出：给定第一个词，第二个词出现的概率$P(average|cats)$
    • 第三个的输出：给定前两个词，第三个词出现的概率$P(15|average,cats)$
  • 标记
    • 句子结尾：/< E O S/>
    • 不名词：/< U N K />
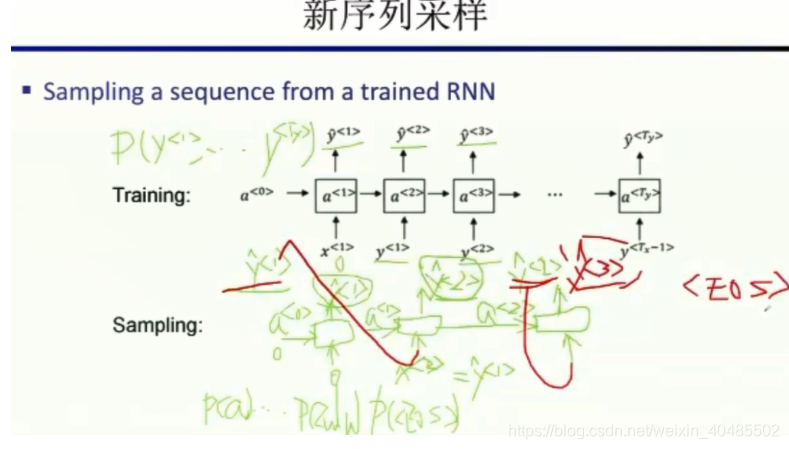
  • 采样可以知道学到了什么）
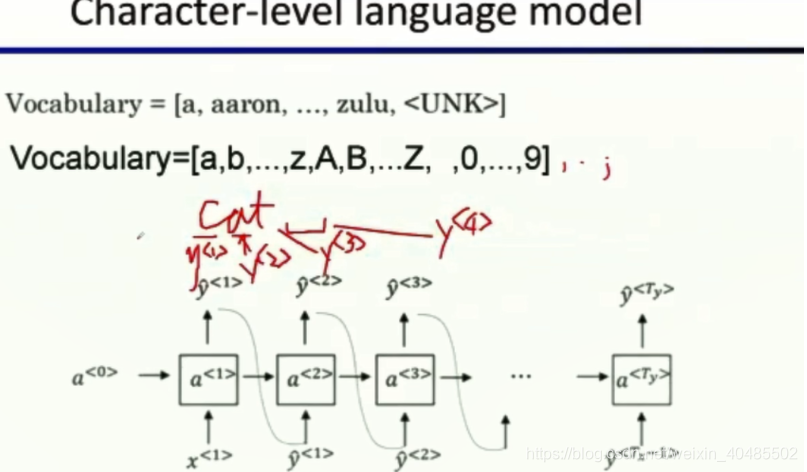
  • 也可以在字符级别建立语言模型–
    • 不会有UNK,但序列很长很长（会梯度下降，计算要求大）
    • 会用在专业词陌生词多的i情况下
  • 不同语料可以训练出不同的文风

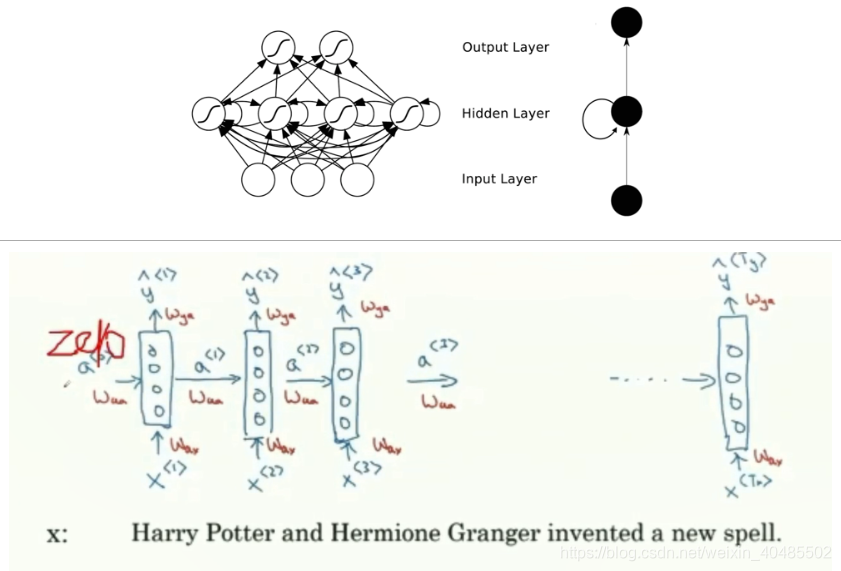
BPTT

BPTT前向传播

• 1对多模型–序列生成任务
  
  

长序列循环神经网络

• BP的困难–回传是线性的
  • error双倍，则回传的错误也是双倍的–>梯度爆炸或消失
    • ${\delta }_a^t=g_1^{\prime }(z_a^t)(W_{ya}^T{\delta }_y^t+W_{a{a}^{\prime }}^T{\delta }_{a^{\prime }}^{t+1})，忽略第一项，看第二项可以知道是线性的$
  • 梯度膨胀（容易发现：
    • （梯度修剪）限制梯度（好解决点
  • 梯度消失（难以发现难以处理–GRU可以解决
• GRU单元
  • 为了保留远时刻的信息
  • 门限循环单元
  • RNN的：
    • 输入层：（常用tanh$a^t=g_1(W_{aa}{a}^{t-1}+W_{ax}{x}^t+b_a)=g_1(W_a[a^{t-1},x^t]+b_a),z_a^t=W_{aa}{a}^{t-1}+W_{ax}{x}^t+b_a$
    • 输出层：（softmax${\hat{y}}^t=g_2(W_{ya}{a}^t+b_y),z_y^t=W_{ya}{a}^t+b_y$
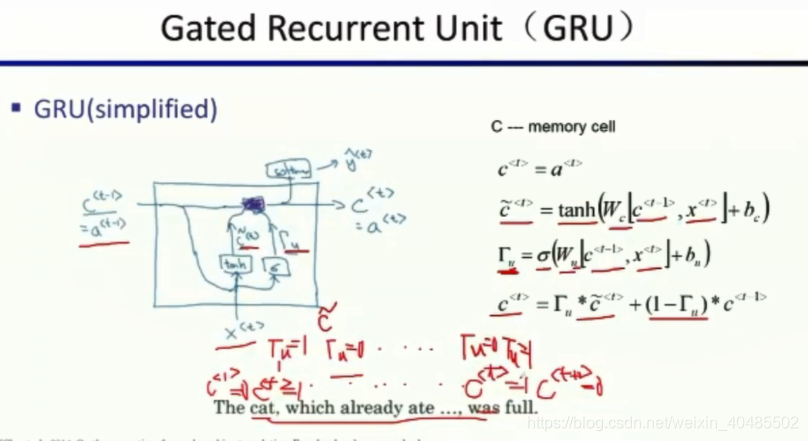
  • GRU（简单版本）：
    • $c^t=a^t$
    • $输入：{\tilde{c}}^t=tanh(W_c[c^{t-1},x^t]+b_c)$–和RNN的输入一样
    • $激活门/更新门：{\Gamma }_u=\sigma (W_u[c^{t-1},x^t]+b_u)$–sigmoid–0/1
    • $c^t={\Gamma }_u\ast {\tilde{c}}^t+(1-{\Gamma }_u)\ast c^{t-1}，{\Gamma }_u=1，更新并遗忘过去$–决定遗忘还是记住过去
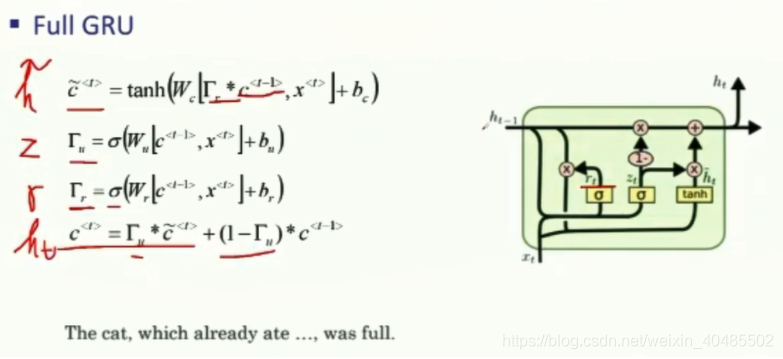
  • GRU（完全）：
    • $c^t=a^t$
    • $输入：{\tilde{c}}^t=tanh(W_c[{\Gamma }_r\ast c^{t-1},x^t]+b_c),$–和RNN的输入一样
    • $输入门：{\Gamma }_r=\sigma (W_r[c^{t-1},x^t]+b_r)$–sigmoid–0/1,备选状态和前一时刻状态是否相关
    • $激活门/更新门：{\Gamma }_u=\sigma (W_u[c^{t-1},x^t]+b_u)$–sigmoid–0/1
    • $c^t={\Gamma }_u\ast {\tilde{c}}^t+(1-{\Gamma }_u)\ast c^{t-1}，{\Gamma }_u=1，更新并遗忘过去$–决定遗忘还是记住过去
  • 有两个门，比LSTM更快、可以扩大模型的规模
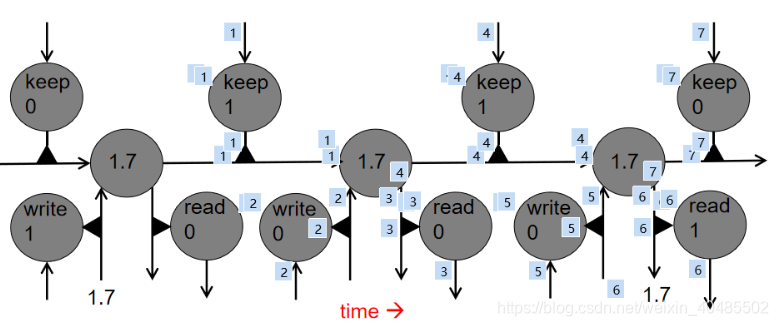
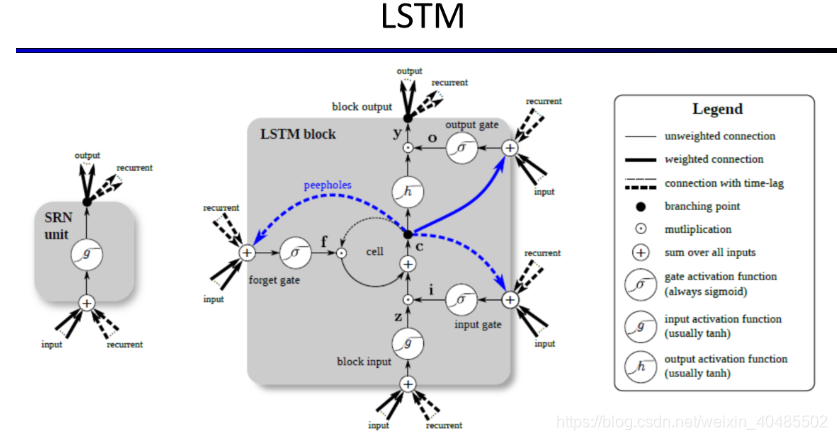
• LSTM长短时记忆
  • 利用逻辑和线性运算来求乘法？
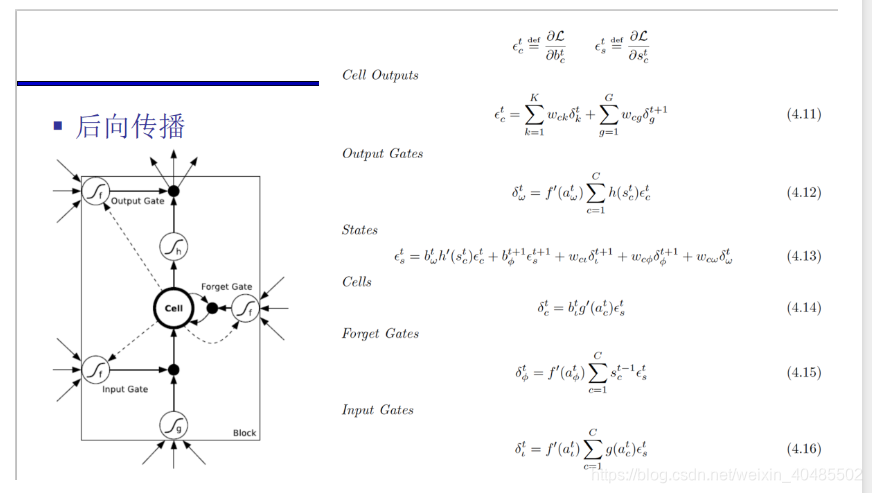
  • BPTT训练
    • 前向
      • 写门（输入门）
        • $a_L^t=W_L^T{x}^t+W_L^T{b}^{t-1}+W_L^T{s}^{t-1},b是输出，x是输入，s是状态（隐层）$
        • $b_L^t=f(a_L^t)$
      • 遗忘门
        • $a_{\varphi }^t=W_{\varphi }^T{x}^t+W_{\varphi }^T{b}^{t-1}+W_{\varphi }^T{s}^{t-1},b是输出，x是输入，s是状态（隐层）$
        • $b_{\varphi }^t=f(a_{\varphi }^t)$
      • cell
        • $a_C^t=W_C^T{x}^t+W_C^T{b}^{t-1},b是输出，x是输入，s是状态（隐层）$
        • $s_C^t=b_{\varphi }^t{s}_C^{t-1}+b_L^{t}g(a_C^t)$
      • 读门（输出门）
        • $a_{\omega }^t=W_{\omega }^T{x}^t+W_{\omega }^T{b}^{t-1}+W_{\omega }^T{s}^{t-1},b是输出，x是输入，s是状态（隐层）$
        • $b_{\omega }^t=f(a_{\omega }^t)$
  • 和GRU比：更强大和灵活，有三个门
• 双向RNN
  • 上下文都用上
• 深层RNN

LSTM

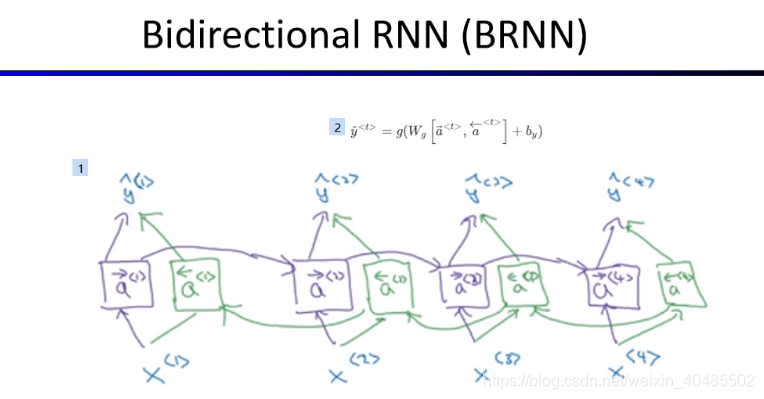
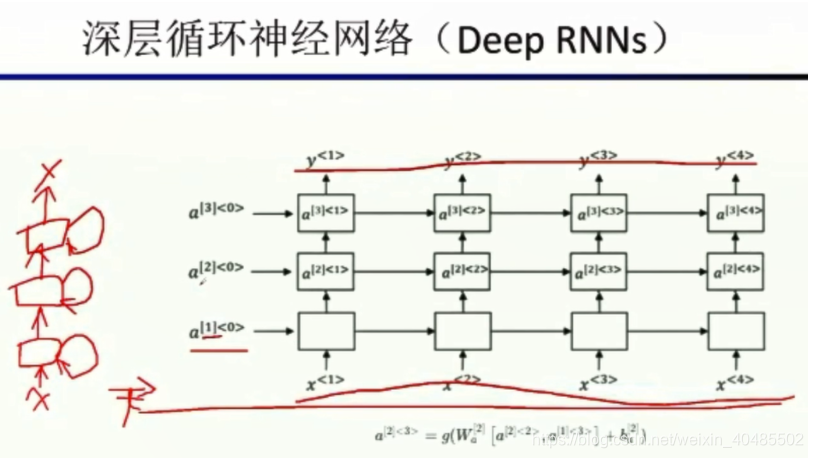
序列到序列的模型

（many to many

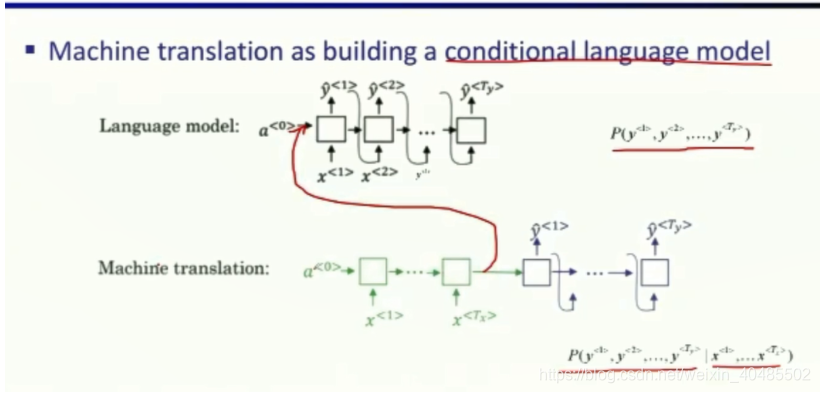
GRU或者LSTM/RNN都可以
采样可能得到多个句子，选择可能性最大的那个

单词表很大，词很多，每一个句子的获得都要搜索很多单词，都产生也不划算
以BFS/DFS搜索效果都不大好—》集束搜索
贪婪搜索会受到常用词影响而不一定是最好的

集束搜索——近似搜索

1. 利用$P(y^1|x)$找到最可能的三个单词（集束宽度B=3)
2. 对这三个单词再看第二个单词有没有合适的
   • 对每个单词分别计算$P(y^1,y^2|x)=P(y^1|x)P(y^2|y^1,x),P(y^2|y^1,x)是神经网络计算出来的$，单词表,10000，这里有30000个组合，再从这里挑出三个最大的组合
3. 重复2

*　集束搜索宽度Ｂ＝１：退化到贪婪搜索

• $B=\infty$：穷举、宽度优先搜索BFS
• 实际应用中：B=10或者50
  

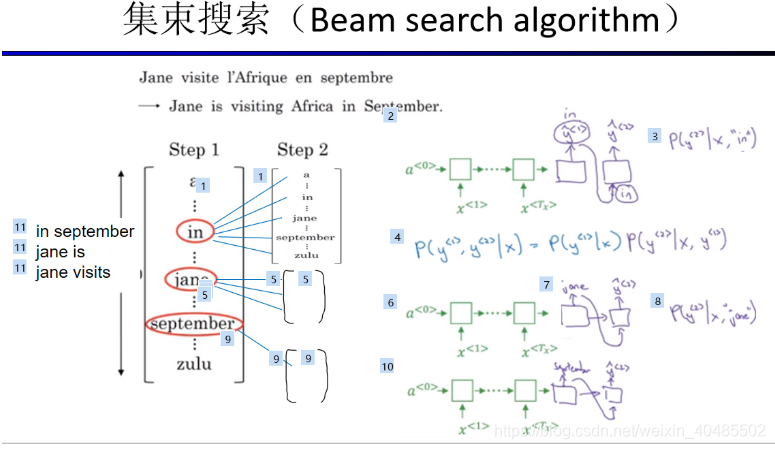
改进的集束搜索

• 长度归一化
  • 以前的：$P(y^1,y^2,...,y^{T_y}|x)=P(y^1|x)P(y^2|y^1,x)...P(y^{T_y}|y^1,y^2,...,y^{T_x-1},x)={\Pi }_{t=1}^{T_y}P(y^t|y^1,y^2,...,y^{t-1},x)$
    • $argma{x}_y{\Pi }_{t=1}^{T_y}P(y^t|y^1,y^2,...,y^{t-1},x)=argma{x}_{y}P(y^1,y^2,...,y^{T_y}|x)$
    • 乘积导致越来越小
  • 解决：log
    • $argma{x}_y{\Sigma }_{t=1}^{T_y}logP(y^t|y^1,y^2,...,y^{t-1},x)$
      • 是负数，所以以乘积或者求和得到的结果，序列越长则数值越小—趋向于选择短序列
    • 所以要归一化：$argma{x}_y\frac{1}{T_y^{\alpha }}{\Sigma }_{t=1}^{T_y}P(y^t|y^1,y^2,...,y^{t-1},x)$
• 目标函数：归一化的对数似然函数
  • $argma{x}_y\frac{1}{T_y^{\alpha }}{\Sigma }_{t=1}^{T_y}P(y^t|y^1,y^2,...,y^{t-1},x)$

集束搜索的误差分析

• $y^{\ast }--人的选择（最优，\hat{y}--算法的选择$
• $P(y^{\ast }|x)>P(\widehat{(}y)|x)$:集束搜索错误了（因为他选的应该是概率最大的
  • 解决：增加B
• $P(y^{\ast }|x)<=P(\widehat{(}y)|x)，y^{\ast }最优，但却预测的小，RNN有问题，P(y^{\ast }|x)<P(\widehat{(}y)|x)$

–>以上结果是多个句子结果比较之后才能判别到底是RNN还是集束搜索的问题

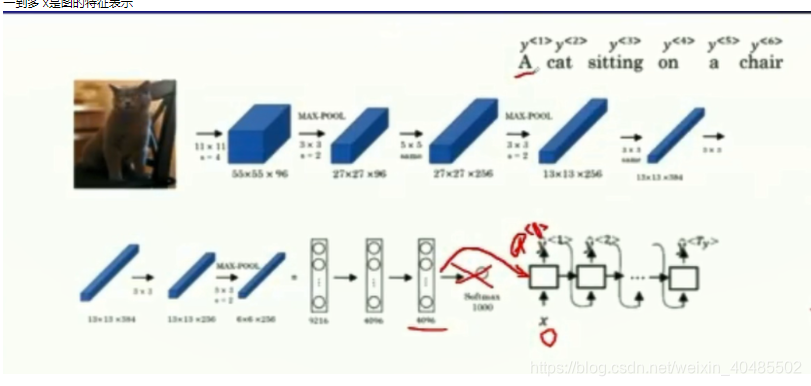
图到文本

一到多
x是图的特征表示

注意力模型

• 对长序列的问题（句子长或短性能都会变差）
  • 长序列不好记忆
  • 每次只考虑一部分，看一部分翻译一部分
• 结构
  • 输入：低层仍是原来的双向RNN,但是输出层不要了（不直接产生输出），只保留隐层输出的向量（表示）
  • 输出，换成了另一个RNN
  • 产生系数的小神经网络也加进去
  • –》一起训练（BP)

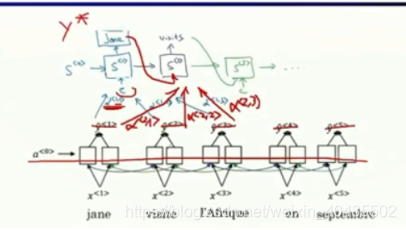
每个c是所有低层输出的线性组合（并非只有图中的三个）

• $c^1={\Sigma }_{t^{\prime }}{\alpha }^{<1,t^{\prime }>}{a}^{<t^{\prime }>},{\Sigma }_{t^{\prime }}{\alpha }^{<1,t^{\prime }>}=1,a是低层的隐藏层的输出$
• ${\alpha }^{<t,t^{\prime }>}=softmax(e^{t,t^{\prime }})=\frac{exp(e^{<t,t^{\prime }>})}{{\Sigma }_{t^{\prime }=1}^{T_x}exp(e^{<t,t^{\prime }>}}$—保证和为1
• $e^{<t,t^{\prime }>}=g(s^{t-1},a^t)$–用一个小的神经网络产生