1.模糊计算

• why模糊
  • 取得精确数据不可能或很困难
  • 没有必要获取精确数据
• 模糊性概念：对象从属的界限是模糊的，随判断人的思维而定
  • 不同人的界定标准不一样
• 隶属函数：使模糊概念数学化
  • 形式化定义：
    • 设U是给定论域，
    • ${\mu }_F$u∈U映射为[0, 1]上某个实值的函数，即
      • ${\mu }_F:U->[0,1]$
    • 则称${\mu }_F$为定义在U上的一个隶属函数，
    • 模糊集：由\mu_F(u)（对所有u∈U）所构成的集合F称为U上的一个模糊集，
      • 离散的
        • ${\mu }_F(ui)=0的可以忽略$
        • 表示1：$F={\mu }_F(u1),{\mu }_F(u2),...,{\mu }_F(un)$
        • 表示2：$F={\mu }_F(u1)/u1+{\mu }_F(u2)/u2+...+{\mu }_F(un)/un$
          • +只是连接，/也不是除号
        • 表示3：$F={\mu }_F(u1)/u1，{\mu }_F(u2)/u2，...，{\mu }_F(un)/un$
        • 表示4：$F=（{\mu }_F(u1)，u1），（{\mu }_F(u2)，u2），...，（{\mu }_F(un)，un）$
      • 连续的$F={\int }_{u\in U}{\mu }_F(u)/u$
    • ${\mu }_F(u)$:称为u对F的隶属度。
      • 越大隶属度越高。
      • 当${\mu }_F(u)仅为0/1时$,F退化为普通集合

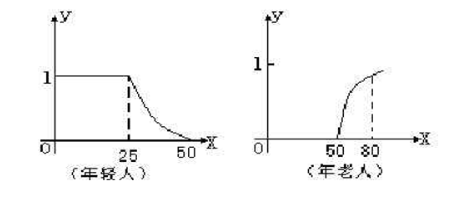
• 区分

  • 模糊性:
    • 事件发生的程度，而不是一个事件是否发生.
  • 随机性:
    • 描述事件发生的不确定性,即,一个事件发生与否.

• 模糊集合之间的关系

  • 相等：$任意u\in U{\mu }_F(u)={\mu }_G(u)<==>F=G$
  • 包含：$任意u\in U{\mu }_F(u)\le {\mu }_G(u)<==>F\subseteq G$
  • 非：¬F=G<==>$任意u\in U{\mu }_F(u)=1-{\mu }_G(u)$
  • 交：$F\cap G<==>{\mu }_{F\cap G}(u)=mi{n}_{u\in U}({\mu }_F(u),{\mu }_G(u))$
  • 交：$F\cup G<==>{\mu }_{F\cup G}(u)=ma{x}_{u\in U}({\mu }_F(u),{\mu }_G(u))$

• 描述数据

  • eg：十个分数：72,68,71,70,86,69,70,82,72,75
    1. 平均分73.5（精确，但不知道分布，不直观
    2. 这次考试成绩在70分左右，个别在80分以上
       • 一些定义：
         • “大多数”
           • 0.5/6+0.8/7+1/8+1/9+1/10
         • “70分左右”
           • 0.5/68+1/69+1/70+1/71+1/72+0.8/73+0.5/74+0.5/75
         • “个别”
           • 1/1+1/2+0.5/3
         • “80分以上”
           • 1/80+1/81+1/82+…+1/100
       • 这句话依据这个定义来看的话
         • 70分左右
           • 1+0.5+1+1+0+1+1+0+1+0.5=7
         • 大多数：7对大多数的隶属度0.8
         • 80分以上：2个人
         • 个别：2 对个别是1

• 笛卡尔积：设V与W是两个普通集合，V与W的笛卡尔乘积为V×W ={(v,w)∣任意$v\in V$，任意$w\in W$}

• 从V到W的关系R：V×W上的一个子集，即 $R\subseteq V\times W$

  • 记为$V\stackrel{R}{\to }W$
  • 对于V×W中的元素(v,w)，若(v,w)∈R，则称v与w有关系R；
  • 若(v,w)$\notin$R，则称v与w没有关系。

• 模糊关系
  

• 关系的合成

  • ${\mu }_{R_{1}o{R}_2}(u,w)=\vee {\mu }_{R_1}(u,v)\wedge {\mu }_{R_2}(v,w)$–max min—先取min再取 max
  • 像矩阵的运算
  • eg：
    • $R1=\left[\begin{array}{ccc}0.4& 0.5& 0.7\\ 0.8& 0.3& 0.7\end{array}\right]$
    • $R2=\left[\begin{array}{cc}0.7& 0.9\\ 0.2& 0.8\\ 0.5& 0.3\end{array}\right]$
    • R1oR2(1,1)=∨{0.4∧0.7,0.2∧0.5,0.6∧0.5}=∨{0.4,0.2,0.5}=0.5R1oR2(1,1)=∨\{0.4∧0.7,0.2∧0.5,0.6∧0.5\}=∨\{0.4,0.2,0.5\}=0.5R1oR2(1,1)=∨{0.4∧0.7,0.2∧0.5,0.6∧0.5}=∨{0.4,0.2,0.5}=0.5
    • $R1oR2=\left[\begin{array}{cc}0.5& 0.5\\ 0.7& 0.8\end{array}\right]$

• 模糊逻辑

  • 模糊逻辑：定义模糊谓词、模糊量词、模糊修饰语等
  • 模糊谓词
    • 设x∈U，F为模糊谓词，即U中的一个模糊关系，则模糊命题可表示为
      • x is F
    • 其中的模糊谓词F可以是大、小、年轻、年老、冷、暖、长、短等。
  • 模糊量词
    • 模糊逻辑中使用的模糊量词，如极少、很少、几个、少数、多数、大多数、几乎所有等
      

笛卡尔积、关系

模糊集

连续的隶属度函数

运算

• 很少有成绩好的学生特别贪玩
  
• 纠正平方后，起止点不变。

2.evolution 遗传算法

• 特点
• 自组织、自适应和自学习性—概率转移准则，非确定性规则
• 本质并行性—群体搜索
  • 独立进化
  • 群体搜索
• 不需要其他知识，只需要影响搜索方向的目标函数和相应的适应度函数