文章目录
- 1.维度、特征与维度灾难
- 维度=特征
- 维度灾难
- 降维
- 1 维度选择
- 3.特征抽取
- 3.1 预备知识
- 3.2 线性模型
- 3.2.1 多维缩放MDS
- 3.2.2 线性降维的一般形式
- 3.2.3 PCA主成分分析
- 3.3 非线性模型
- 3.3.1KPCA
- 3.3.2流行学习(欧氏距离不能反映相似性)
- 3.3.3 拉普拉斯特征映射(Laplacian Eigenmap)
- 3.3.4 自编码器
- RBM-逐层训练
- 3.3.5 word2vec
1.维度、特征与维度灾难
- 维度=特征
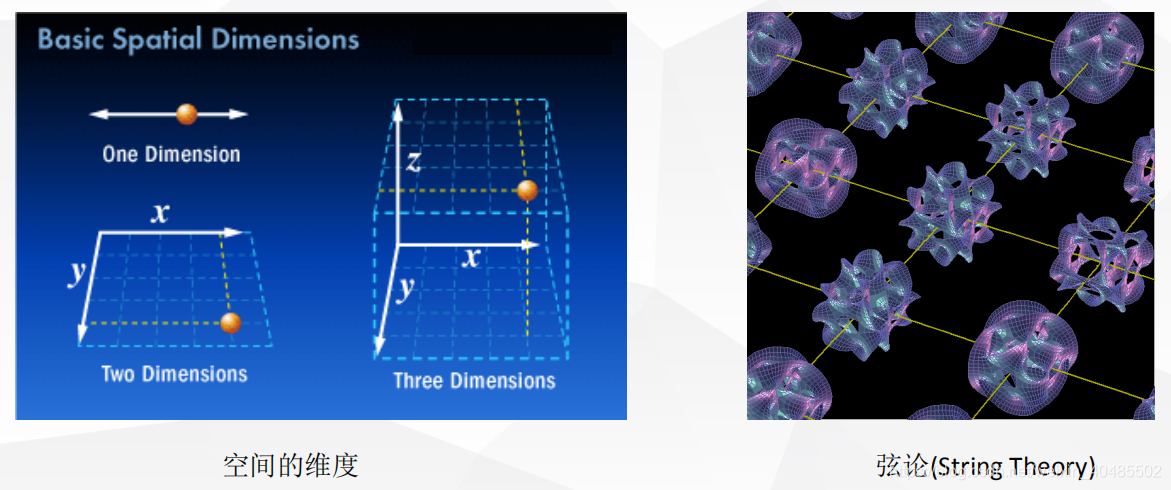
- 数据空间的维度可能非常大
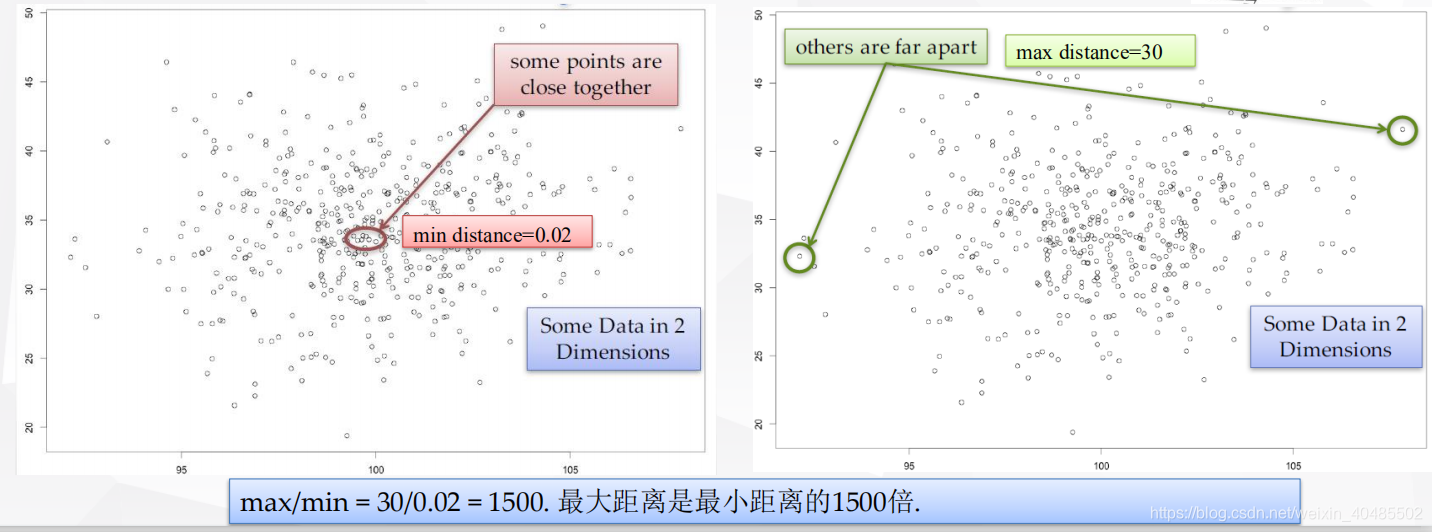
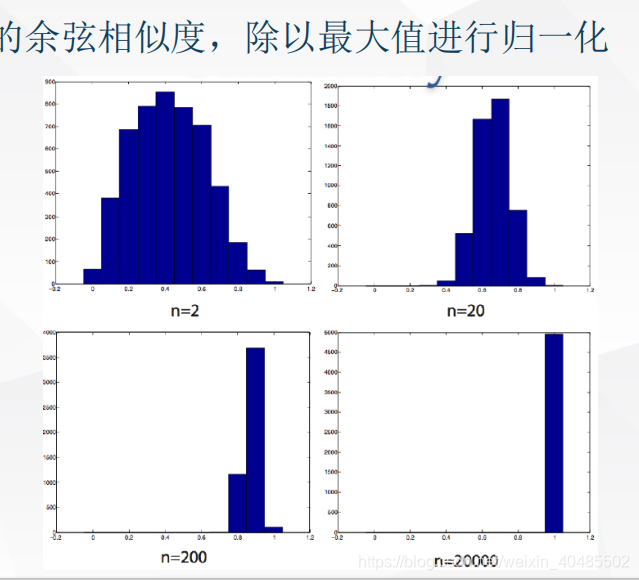
- 维度灾难:随着空间维度的增长,数据点越来越分散,以至于距离和密度的概念变得越来越模糊
- 没有一种距离函数或相似性函数能避免高维带来的问题
- 何时有影响
- 当我们使用的算法需要用到距离和相似性计算时
- 尤其对于聚类和k近邻算法
- 由于共线性引起的问题,希望得到一个简单模型
- 冗余特征
- 算法的计算和存储复杂度成为难题
- 当我们使用的算法需要用到距离和相似性计算时
- 解决方案:降维/嵌入
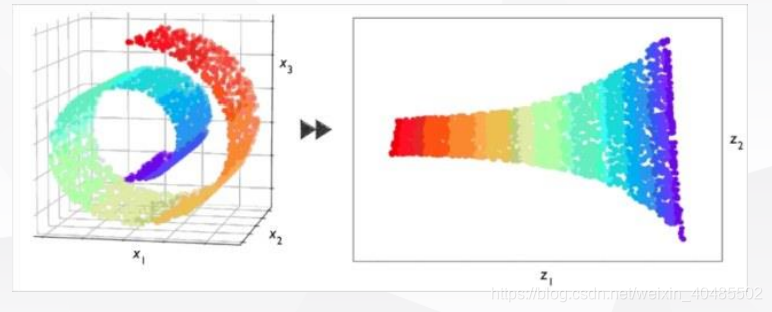
- 降维或嵌入:是指将原始的高维数据映射到低维空间
- 实质的想法: 高度冗余的数据通常是可以被压缩的, 即高维复杂的数据其在的维度可能比较小,或者和任务相关的维度较小(秩小)
- 要求:原md维的矩阵,m个样本,d维特征–>md’(d’<<d)
- 方法
- 维度选择:选择已有维度的一个子集
- 维度抽取:通过组合已有的维度构建新的维度
- 降维的思想:最小化重建误差==>最大化z的方差
| 怎么做 | 优点 | 缺点 | |
|---|---|---|---|
| 采样 | 随机选择 | 简单,流行,泛化性能好 | 没有精度保证,差的可能错误很大,稀疏数据上大多为0 |
| 手工 | 手工移除(冗余、不相关、质量差) | - | - |
| 监督方法 | 训练多个单特征分类器,估计互信息,统计每个特征和类别之间的独立性(前向/后向) | 自动 | - |
| 算法 | 问题 | 目标函数 | 优点 | |
|---|---|---|---|---|
| MDS | 由距离D矩阵–>dist–>B(bij=−12(distij2−disti⋅2−dist⋅j2+dist⋅⋅2)b_{ij}=-\frac{1}{2}(dist_{ij}^2-dist_{i·}^2-dist_{·j}^2+dist_{··}^2)bij=−21(distij2−disti⋅2−dist⋅j2+dist⋅⋅2))–特征分解,得到特征矩阵截取特征矩阵->Z=Σ∗1/2V∗T∈Rd∗∗mZ=\Sigma_*^{1/2}V_*^T \in R^{d^**m}Z=Σ∗1/2V∗T∈Rd∗∗m | 线性 | 原距离=新距离 | |
| 一般形式 | z=WTxz=W^Txz=WTx | 如何选择W? 线性 | - | 线性 |
| PCA | z=WTx,W为XXT的前d′特征向量组成的矩阵,W=U′z=W^Tx,W为XX^T的前d'特征向量组成的矩阵,W=U'z=WTx,W为XXT的前d′特征向量组成的矩阵,W=U′ | 只用了二阶统计量,不能处理高阶依赖;受限于线性投影 | 最小化重建误差min∥x−x~∥min\|x-\tilde{x}\|min∥x−x~∥ | 特征向量的方法;无额外参数;无迭代;无局部最小值 |
| 算法 | 目标函数 | |
|---|---|---|
| KPCA | K-去中心后特征值分解得到特征向量α;zj=Σi=1mαijk(xi,x)特征向量\alpha;z^j=\Sigma_{i=1}^m\alpha^j_ik(x_i,x)特征向量α;zj=Σi=1mαijk(xi,x) | 最小化重构误差 |
| ISOMAP | 依据邻近点得到邻接图-最短路径-距离矩阵D-MDS得到结果 | 原距离=现在的距离 |
| 拉普拉斯特征映射 | 构建邻接图;求L的特征值Z | Σi,j=1m(zi−zj)2wij−>zTLz,S.T.ZTDZ=I,ZTDI=0\Sigma_{i,j=1}^m(z^i-z^j)^2w_{ij}->z^TLz,S.T.Z^TD^Z=I,Z^TD^I=0Σi,j=1m(zi−zj)2wij−>zTLz,S.T.ZTDZ=I,ZTDI=0 |
| 自编码器 | minw∈Rd∗d′Σi=1m∥xi−WTWxi∥2min_{w\in R^{d*d'}}\Sigma_{i=1}^m\|x_i-W^TWx_i\|^2minw∈Rd∗d′Σi=1m∥xi−WTWxi∥2,比PCA可以学习更加有效的表达 | |
| word embedding(word2vec) | ||
| skip-gram | 极大似然估计Lskip−gram=1TΣt=1TΣ−c≤j≤c.j≠ologp(wt+j∥wt)L_{skip-gram}=\frac{1}{T}\Sigma_{t=1}^T\Sigma_{-c\leq j \leq c.j\neq o}log p(w_{t+j}\|w_t)Lskip−gram=T1Σt=1TΣ−c≤j≤c.j=ologp(wt+j∥wt) | |
| cbow | 极大似然估计Lskip−gram=1TΣt=1Tlogp(wt∥wt∗)L_{skip-gram}=\frac{1}{T}\Sigma_{t=1}^Tlog p(w_{t}\|w_{t*})Lskip−gram=T1Σt=1Tlogp(wt∥wt∗) |
| 方法 | 思想 | |
|---|---|---|
| MDS或ISOMAP | 全局嵌入方法 | 通过保持所有样本点对之间的欧氏距离或测地线距离来计算嵌入表达 |
| 局部线性嵌入LLE | 局部嵌入方法 | 保持局部集合特性来恢复全局的非线性结构 (基本原理:利用局部邻居的重叠特性,协同计算,可以得到全局的集合信息) |
| 拉普拉斯特征映射 | 局部嵌入方法 | 保持局部集合特性来恢复全局的非线性结构 (基本原理:利用局部邻居的重叠特性,协同计算,可以得到全局的集合信息) |
维度=特征

维度灾难

降维


1 维度选择
- 采样
- 随机选择
- x1Tx2=Σj=1dx1jx2j≈(x~1Tx~2=Σj=1d′x~1jx~2j)∗dd′x_1^Tx_2=\Sigma_{j=1}^dx_{1j}x_{2j} \approx (\tilde{x}_1^T \tilde{x}_2=\Sigma_{j=1}^{d'}\tilde{x}_{1j}\tilde{x}_{2j})*\frac{d}{d'}x1Tx2=Σj=1dx1jx2j≈(x~1Tx~2=Σj=1d′x~1jx~2j)∗d′d
- 手工
- 移除:
- 冗余(多重共线性、方差膨胀引子VIFs
- 不相关(文本挖掘中的停用词
- 质量差的特征( 值得缺失比超过百分之五十)
- 移除:
- 监督方法
- 为每个特征打分: •
- 训练或者交叉验证单特征分类器
- 估计每个特征和分类label的互信息
- 用χ2 统计量度量每个特征和类别之间的独立性
- 搜索有用的特征子集
- 前向
- 从零个特征开始
- 一遍式(one pass)或者迭代式(iterative)地选择
- 后向
- 从所有特征开始
- 一遍式或迭代式地选择


- 前向
- 为每个特征打分: •
3.特征抽取
3.1 预备知识
- 矩阵
- 矩阵的秩
- 迹=对角线上元素的和
- 矩阵分解–一个矩阵费解成几个矩阵的乘法
- 高维数据的低秩逼近
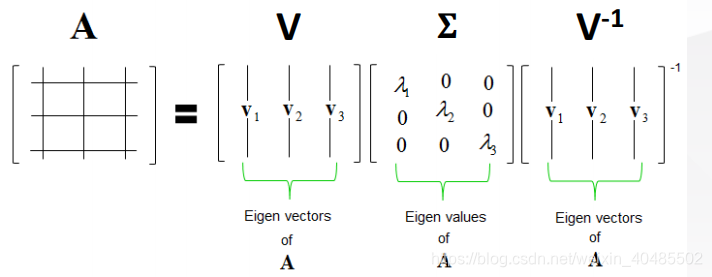
- 特征分解Av=λv;A=VΣV−1,A:m∗mAv=\lambda v;A=V\Sigma V^{-1},A:m*mAv=λv;A=VΣV−1,A:m∗m
- 奇异值分解(SVD)A=Σi=1rσiuiviT=UΣVTU、V是正交矩阵A=\Sigma_{i=1}^r\sigma_iu_iv_i^T=U\Sigma V^T\\U、V是正交矩阵A=Σi=1rσiuiviT=UΣVTU、V是正交矩阵
- U(V)–每个列或每个行代表一个方向
- 列(行)之间相互正交
- 将Σ\SigmaΣ中奇异值按降序排列,对应特征向量也对应改变
- 则u1:最大能量方向u2:与u1正交的最大能量方向u3:与u1和u2正交的最大能量方向u_1:最大能量方向\\u_2:与u_1正交的最大能量方向\\u_3:与u_1和u_2正交的最大能量方向u1:最大能量方向u2:与u1正交的最大能量方向u3:与u1和u2正交的最大能量方向
- 特征值、方差的意义
- 统计:方差
- 物理:能量
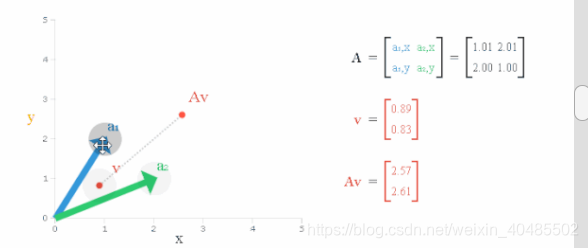
- 矩阵乘法–线性变换
- horizontal shear
- 平移
- squeeze mapping(伸缩变性
- scaling(等比例缩放
- rotation旋转



3.2 线性模型

3.2.1 多维缩放MDS
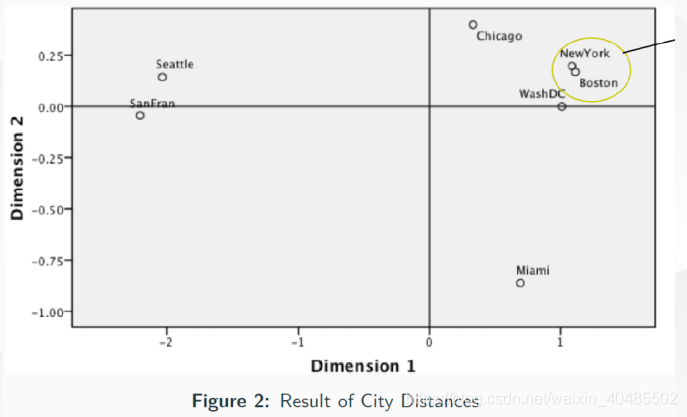
- 多维缩放(Multiple Dimensional Scaling,简称MDS)
- 问题形式化:
- 给定空间中任意两个点的距离( pairwise distances ), 点的精确坐标和维度是未知的.
- 我们希望将这些点嵌入到一个低维的空间中,使得新的空间中点对之间的距离和原始空间中的距离尽可能接近.
- 显然,投影到低维空间的形式不是唯一的,原因是低维空间的点经过平移(translation),旋转(rotation)和对称(reflection)后,点对之间的距离不变
- 基本想法: d′空间的欧式距离等于原始空间的欧式距离∣∣zi−zj∣∣=distij,distij=Dij||z_i-z_j||=dist_{ij},dist_{ij}=D_{ij}∣∣zi−zj∣∣=distij,distij=Dij
- 推导:
- B=ZTZ∈Rm∗m,bij=ziTzjdistij2=∣∣zi∣∣2+∣∣zj∣∣2−2ziTzj=bii+bjj−2bijΣi=1mzi=0Σi=1mdistij2=tr(B)+mbjj=mdist⋅j2Σj=1mdistij2=tr(B)+mbii=mdisti⋅2Σi=1mΣj=1mdistij2=2mtr(B)=mdist⋅⋅2=Σi=1mtr(B)+Σi=1mbii=mtr(B)=mtrb(B)bij=−12(distij2−bii−bjj)=−12(distij2−1m(Σj=1mdistij2−tr(B))−1m(Σi=1mdistij2−tr(B)))=−12(distij2−1mΣj=1mdistij2−1mΣi=1mdistij2+2mtr(B))=−12(distij2−1mΣj=1mdistij2−1mΣi=1mdistij2+1m2Σi=1mΣj=1mdistij2)=−12(distij2−disti⋅2−dist⋅j2+dist⋅⋅2)B=Z^TZ\in R^{m*m},b_ij=z_i^Tz_j\\dist_{ij}^2=||z_i||^2+||z_j||^2-2z_i^Tz_j=b_{ii}+b_{jj}-2b_{ij}\\\Sigma_{i=1}^mz_i=0\\\Sigma_{i=1}^mdist_{ij}^2=tr(B)+mb_{jj}=mdist_{·j}^2\\\Sigma_{j=1}^mdist_{ij}^2=tr(B)+mb_{ii}=mdist_{i·}^2\\\Sigma_{i=1}^m\Sigma_{j=1}^mdist_{ij}^2=2mtr(B)=mdist_{··}^2=\Sigma_{i=1}^mtr(B)+\Sigma_{i=1}^mb_{ii}=mtr(B)=mtrb(B)\\b_{ij}=-\frac{1}{2}(dist_{ij}^2-b_{ii}-b_{jj})\\=-\frac{1}{2}(dist_{ij}^2-\frac{1}{m}(\Sigma_{j=1}^mdist_{ij}^2-tr(B))-\frac{1}{m}(\Sigma_{i=1}^mdist_{ij}^2-tr(B)))\\=-\frac{1}{2}(dist_{ij}^2-\frac{1}{m}\Sigma_{j=1}^mdist_{ij}^2-\frac{1}{m}\Sigma_{i=1}^mdist_{ij}^2+\frac{2}{m}tr(B))\\=-\frac{1}{2}(dist_{ij}^2-\frac{1}{m}\Sigma_{j=1}^mdist_{ij}^2-\frac{1}{m}\Sigma_{i=1}^mdist_{ij}^2+\frac{1}{m^2}\Sigma_{i=1}^m\Sigma_{j=1}^mdist_{ij}^2)\\=-\frac{1}{2}(dist_{ij}^2-dist_{i·}^2-dist_{·j}^2+dist_{··}^2)B=ZTZ∈Rm∗m,bij=ziTzjdistij2=∣∣zi∣∣2+∣∣zj∣∣2−2ziTzj=bii+bjj−2bijΣi=1mzi=0Σi=1mdistij2=tr(B)+mbjj=mdist⋅j2Σj=1mdistij2=tr(B)+mbii=mdisti⋅2Σi=1mΣj=1mdistij2=2mtr(B)=mdist⋅⋅2=Σi=1mtr(B)+Σi=1mbii=mtr(B)=mtrb(B)bij=−21(distij2−bii−bjj)=−21(distij2−m1(Σj=1mdistij2−tr(B))−m1(Σi=1mdistij2−tr(B)))=−21(distij2−m1Σj=1mdistij2−m1Σi=1mdistij2+m2tr(B))=−21(distij2−m1Σj=1mdistij2−m1Σi=1mdistij2+m21Σi=1mΣj=1mdistij2)=−21(distij2−disti⋅2−dist⋅j2+dist⋅⋅2)
- 对B做特征分解B=VΣVTΣ=diag(λ1,λ2,...,λd)Σ∗=diag(λ1,λ2,...,λd∗),λ1>λ2>...>λd∗V∗对应特征向量组成的矩阵Z=Σ∗1/2V∗T∈Rd∗∗m(d∗<<d)B=V\Sigma V^T\\\Sigma=diag(\lambda_1,\lambda_2,...,\lambda_d)\\\Sigma_*=diag(\lambda_1,\lambda_2,...,\lambda_{d^*}),\lambda_1>\lambda_2>...>\lambda_{d^*}\\V_*对应特征向量组成的矩阵\\Z=\Sigma_*^{1/2}V_*^T \in R^{d^**m}(d^*<<d)B=VΣVTΣ=diag(λ1,λ2,...,λd)Σ∗=diag(λ1,λ2,...,λd∗),λ1>λ2>...>λd∗V∗对应特征向量组成的矩阵Z=Σ∗1/2V∗T∈Rd∗∗m(d∗<<d)
- 算法
- 原来距离dist(矩阵D),B是中间矩阵
- 目标:得到z,维度d*
- 由距离D矩阵–>dist–>B
- bij=−12(distij2−disti⋅2−dist⋅j2+dist⋅⋅2)b_{ij}=-\frac{1}{2}(dist_{ij}^2-dist_{i·}^2-dist_{·j}^2+dist_{··}^2)bij=−21(distij2−disti⋅2−dist⋅j2+dist⋅⋅2)
- 特征分解,得到特征矩阵
- 截取特征矩阵->Z=Σ∗1/2V∗T∈Rd∗∗mZ=\Sigma_*^{1/2}V_*^T \in R^{d^**m}Z=Σ∗1/2V∗T∈Rd∗∗m
3.2.2 线性降维的一般形式
- 数据X–d*m
- 新的数据Z–d’*m
- 选择d’方向向量W
- z=WTxz=W^Txz=WTx
- 问题:如何选择W?
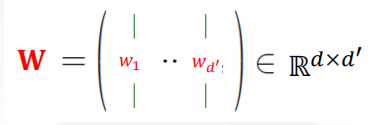
3.2.3 PCA主成分分析
- 目标函数:最小化重建误差和minW∈Rd∗d′Σi=1m∥xi−Wzi∥2min_{W\in R^{d*d'}}\Sigma_{i=1}^m\|x_i-Wz_i\|^2minW∈Rd∗d′Σi=1m∥xi−Wzi∥2
- ∣∣wi∣∣=1,wiTwj=0(i≠j)||w_i||=1,w_i^Tw_j=0(i\neq j)∣∣wi∣∣=1,wiTwj=0(i=j)–新的坐标系
- 编码:zi=WTxi,zij=wjTxi解码:x~i=Wzi=Σj=1d′zijwj目标函数:min∣∣x−x~∣∣编码:z_i=W^Tx_i,z_{ij}=w_j^Tx_i\\解码:\tilde{x}_i=Wz_i=\Sigma_{j=1}^{d'}z_{ij}w_j\\目标函数:min||x-\tilde{x}||编码:zi=WTxi,zij=wjTxi解码:x~i=Wzi=Σj=1d′zijwj目标函数:min∣∣x−x~∣∣
- 推导
- Σi=1m∥xi−Wzi∥2=Σi=1m∥xi−Σj=1d′zijwj∥2=Σi=1mziTzi−2Σi=1mziTWTxi+const∝−tr(WT(Σi=1mxixiT)W)=−tr(WTXXTW)\Sigma_{i=1}^m\|x_i-Wz_i\|^2\\= \Sigma_{i=1}^m\|x_i-\Sigma_{j=1}^{d'}z_{ij}w_j\|^2\\=\Sigma_{i=1}^mz_i^Tz_i-2\Sigma_{i=1}^mz_i^TW^Tx_i+const\\∝-tr(W^T(\Sigma_{i=1}^mx_ix_i^T)W)=-tr(W^TXX^TW)Σi=1m∥xi−Wzi∥2=Σi=1m∥xi−Σj=1d′zijwj∥2=Σi=1mziTzi−2Σi=1mziTWTxi+const∝−tr(WT(Σi=1mxixiT)W)=−tr(WTXXTW)
- 最小化重建误差–>最大化样本投影的方差maxΣiziTzi=maxwtr(WTXXTW),s.t.WTW=1max \Sigma_i z_i^Tz_i=max_w tr(W^TXX^TW),s.t.W^TW=1maxΣiziTzi=maxwtr(WTXXTW),s.t.WTW=1
- 拉格朗日方法
- L=tr(WTXXTW)−Σi=1dλi(wiTwi−1)∂tr(WAWT)∂W=2WA,A=AT∂L∂WT=0,则XXTW=λW−−W是XXT的特征向量L= tr(W^TXX^TW)-\Sigma_{i=1}^d\lambda_i(w_i^Tw_i-1)\\\frac{\partial tr(WAW^T)}{\partial W}=2WA,A=A^T\\\frac{\partial L}{\partial W^T}=0,则XX^TW=\lambda W--W是XX^T的特征向量L=tr(WTXXTW)−Σi=1dλi(wiTwi−1)∂W∂tr(WAWT)=2WA,A=AT∂WT∂L=0,则XXTW=λW−−W是XXT的特征向量
- 拉格朗日方法
- 思想:
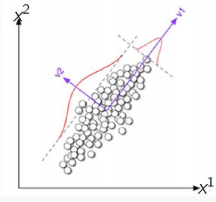
- 目标是捕捉数据的内在变化
- 中心思想: 寻找一个方向向量,使得数据投影到其上后方差最大
- 如果能找到,继续寻找下一个方向向量,该向量正交于之前的方向向量,并 且尽可能保持数据方差
- 如果足够幸运,我们能够找到一些这样的方向向量,称为主成分,它们可以 用来精确的描述数据。
- 算法:
- 均值化为0:xi=xi−1mΣj=1mxj−−−这是所有样本的均值,若有多类,则是多类样本均值之和x_i=x_i-\frac{1}{m}\Sigma_{j=1}^mx_j---这是所有样本的均值,若有多类,则是多类样本均值之和xi=xi−m1Σj=1mxj−−−这是所有样本的均值,若有多类,则是多类样本均值之和
- 计算XXTXX^TXXT
- 对C=XXTC=XX^TC=XXT特征分解(SVD取U)(C-协方差)
- 取前d‘个特征向量:W=(w1,w2,...,wd′)W=(w_1,w_2,...,w_{d'})W=(w1,w2,...,wd′)
- z=WTxz=W^Txz=WTx
- 特征值算的慢–算SVD
- U=W(取前d’个u)
- d’如何确定?
- 通过简单的分类器KNN通过交叉验证
- 重建阈值Σi=1d"λiΣj=1dλj≥t(eg,方差的85%)\frac{\Sigma_{i=1}^{d"}\lambda_i}{\Sigma_{j=1}^{d}\lambda_j}\geq t(eg,方差的85\%)Σj=1dλjΣi=1d"λi≥t(eg,方差的85%)
- 应用:
- 人脸识别
- LSI:uk第k个主题下的坐标,vi:第i个文档用k个主题表示u_k第k个主题下的坐标,v_i:第i个文档用k个主题表示uk第k个主题下的坐标,vi:第i个文档用k个主题表示
- 优点:
- 特征向量方法
- 没有额外要调节的参数
- 没有迭代
- 没有局部最小值
- 弱点:
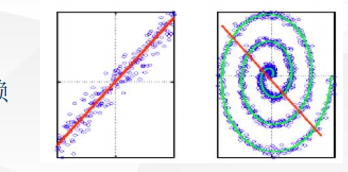
- 只用了二阶统计量,不能处理高阶依赖
- 受限于线性投影
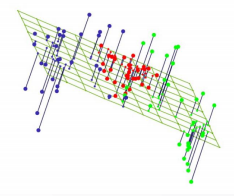
- 非线性下表现不好,子空间是线性的
- S={(x1,x2):x1=w1z,x2=w2z}={(x1,x2):x2=w1w2x1}S=\{(x1,x2):x1=w1z,x2=w2z\}\\=\{(x1,x2):x2=\frac{w1}{w2}x1\}S={(x1,x2):x1=w1z,x2=w2z}={(x1,x2):x2=w2w1x1}




3.3 非线性模型
3.3.1KPCA
- why可以用核
- 因为PCA只需要内积K=XTXK=X^TXK=XTX即可(与SVMs相似
- max∣∣w∣∣=1(WTXXTW)=maxαTxTxα=1αT(XTX)(XTX)αmax_{||w||=1} (W^T X X^TW)=max_{\alpha^Tx^Tx\alpha=1}\alpha^T(X^TX)(X^TX)\alphamax∣∣w∣∣=1(WTXXTW)=maxαTxTxα=1αT(XTX)(XTX)α
- 核函数要求
- 对应的核矩阵是半正定的
- 常见核函数–直观上度量相似度
- 线性核k(x1,x2)=x1Tx2k(x_1,x_2)=x_1^Tx_2k(x1,x2)=x1Tx2
- 多项式核k(x1,x2)=(1+x1Tx2)2k(x_1,x_2)=(1+x_1^Tx_2)^2k(x1,x2)=(1+x1Tx2)2
- 高斯核k(x1,x2)=e−∣∣x1−x2∣∣2k(x_1,x_2)=e^{-||x_1-x_2||^2}k(x1,x2)=e−∣∣x1−x2∣∣2
- Mercer定理:总存在高维特征空间Φ使K(x1,x2)=Φ(x1)TΦ(x2)\Phi使K(x_1,x_2)=\Phi(x_1)^T\Phi(x_2)Φ使K(x1,x2)=Φ(x1)TΦ(x2)
- 算法:
- 计算K, 𝐾𝑖𝑗 = 𝑘(𝑥𝑖, 𝑥𝑗)
- 获得中心化的K:Kˉ\bar{K}Kˉ
- 对Kˉ\bar{K}Kˉ做特征分解
- 选择𝑑′ 个最大的特征值对应的特征向量𝛼
- zj=wjTPhi(x)=Σi=1mαijΦ(xi)TΦ(x)=Σi=1mαijk(xi,x)z^j=w_j^TPhi(x)=\Sigma_{i=1}^m\alpha^j_i\Phi(x_i)^T\Phi(x)\\=\Sigma_{i=1}^m\alpha^j_ik(x_i,x)zj=wjTPhi(x)=Σi=1mαijΦ(xi)TΦ(x)=Σi=1mαijk(xi,x)–新样本第j个成分
3.3.2流行学习(欧氏距离不能反映相似性)
- 流形:是个局部具有欧氏距离的拓扑空间
- 流行能够近似好地任意高维空间的子空间
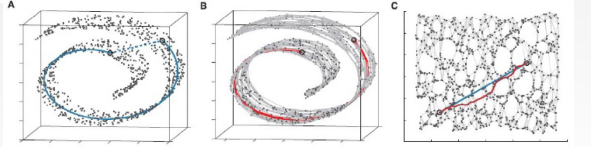
- 高维空间中如何度量距离
- 测地线距离(Geodesic Distance)
- 邻近的点(以欧氏距离近似
- 最远的点(通过一系列邻近点抵达
- 测地线距离(Geodesic Distance)
- ISOMAP:基于metric MDS,试图保留测地距离蕴含的几何结构
- 算法步骤
- 构建邻接图
- 通过连接距离小于𝜖(𝜖 − ISOMAP)的两个点i 和j在N个数据点上定义图G, 或者i 是j的k近邻之一(k-lSOMAP).
- 设置边的长度为d(i,j)
- 计算最短路径
- 初始化dG(i,j)d_G(i,j)dG(i,j) = 𝑑(𝑖,𝑗) 如果i和j相连接,否则dG(i,j)d_G(i,j)dG(i,j)= ∞
- 对于每一个𝑘 = 1,2, … . 𝑁,替换所有的dG(i,j)=min(dG(i,j),dG(i,k)+dG(k,j)d_G(i,j)=min(d_G(i,j),d_G(i,k)+d_G(k,j)dG(i,j)=min(dG(i,j),dG(i,k)+dG(k,j)). 那么DG=[dG(i,j)]D_G = [d_G(i,j)]DG=[dG(i,j)] 包含G中所有点对的最短路径
- 构建低维嵌入
- 通过MDS构建低维的数据嵌入
- bij=−12(distij2−disti⋅2−dist⋅j2+dist⋅⋅2)b_{ij}=-\frac{1}{2}(dist_{ij}^2-dist_{i·}^2-dist_{·j}^2+dist_{··}^2)bij=−21(distij2−disti⋅2−dist⋅j2+dist⋅⋅2)
- 对于新数据点, 我们可以训练一个回归模型给定原数据点去预测新的数据点
- 通过MDS构建低维的数据嵌入
- 构建邻接图
- 瓶颈
- 最短路径
- floyd:O(N3)O(N^3)O(N3)
- dijkstra(fibonacci堆):O(KN2logN)−−K近邻O(KN^2logN)--K近邻O(KN2logN)−−K近邻
- 特征分解O(N3)O(N^3)O(N3)
- 最短路径
| 方法 | 思想 | |
|---|---|---|
| MDS或ISOMAP | 全局嵌入方法 | 通过保持所有样本点对之间的欧氏距离或测地线距离来计算嵌入表达 |
| 局部线性嵌入LLE | 局部嵌入方法 | 保持局部集合特性来恢复全局的非线性结构 (基本原理:利用局部邻居的重叠特性,协同计算,可以得到全局的集合信息) |
| 拉普拉斯特征映射 | 局部嵌入方法 | 保持局部集合特性来恢复全局的非线性结构 (基本原理:利用局部邻居的重叠特性,协同计算,可以得到全局的集合信息) |
K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。该方法的思路是:在特征空间中,如果一个样本附近的k个最近(即特征空间中最邻近)样本的大多数属于某一个类别,则该样本也属于这个类别。

3.3.3 拉普拉斯特征映射(Laplacian Eigenmap)
- 类似ISOMAP,首先构建一个带权图–邻接关系
- 基于图计算特征映射
- 边的创建:
- 𝜀邻域(𝜀 − 𝑛𝑒𝑖𝑔ℎ𝑏𝑜𝑟ℎ𝑜𝑜𝑑):
- 如果 ||𝒙 𝑖 − 𝒙 𝑗 || < 𝜀 (𝜀𝜖ℝ+),节点i 和 j 连一条边
- K近邻(K nearest neighbors):
- 如果𝒙(𝑖)是𝒙(𝑗)的K个最近邻之一或者𝒙(𝑗)是𝒙(𝑖)的K个最近邻之一,则节点 i 和 j 连一条边
- 边权重
- 热核:wij={exp(−∣∣xi−xjσ2)如果i、j相连0otherwisew_{ij}=\begin{cases}exp(-\frac{||x^i-x^j}{\sigma^2})& 如果i、j相连\\0& otherwise\end{cases}wij={exp(−σ2∣∣xi−xj)0如果i、j相连otherwise
- 二值话权重wij={1如果i、j相连0otherwisew_{ij}=\begin{cases}1& 如果i、j相连\\0& otherwise\end{cases}wij={10如果i、j相连otherwise
- 𝜀邻域(𝜀 − 𝑛𝑒𝑖𝑔ℎ𝑏𝑜𝑟ℎ𝑜𝑜𝑑):
- 构建特征映射
- 如果上面构建的图不连通,下列方法单独用于每一个连通分量
- 我们首先考虑寻找一维嵌入向量的特殊情况,然后泛化到一般的d’维的情况
- 一维z
- z=(z1,z2,...,zm)Tz=(z^1,z^2,...,z^m)^Tz=(z1,z2,...,zm)T–一维嵌入向量
- 最小化目标函数Σi,j=1m(zi−zj)2wij\Sigma_{i,j=1}^m(z^i-z^j)^2w_{ij}Σi,j=1m(zi−zj)2wij
- 12Σi,j=1m(zi−zj)2wij=12Σi,j=1m(zi)2wij+12Σi,j=1m(zj)2wij−Σi,j=1m(zi)(zj)wij=Σi,j=1m(zi)2dii−Σi,j=1m(zi)(zj)wij=Σi,j=1mzi(dij−wij)zj=zT(D−W)z=zTLzL=D−W是拉普拉斯矩阵\frac{1}{2}\Sigma_{i,j=1}^m(z^i-z^j)^2w_{ij}\\=\frac{1}{2}\Sigma_{i,j=1}^m(z^i)^2w_{ij}+\frac{1}{2}\Sigma_{i,j=1}^m(z^j)^2w_{ij}-\Sigma_{i,j=1}^m(z^i)(z^j)w_{ij}\\=\Sigma_{i,j=1}^m(z^i)^2d_{ii}-\Sigma_{i,j=1}^m(z^i)(z^j)w_{ij}\\=\Sigma_{i,j=1}^mz^i(d_{ij}-w_{ij})z^j\\=z^T(D-W)z=z^TLz\\L=D-W是拉普拉斯矩阵21Σi,j=1m(zi−zj)2wij=21Σi,j=1m(zi)2wij+21Σi,j=1m(zj)2wij−Σi,j=1m(zi)(zj)wij=Σi,j=1m(zi)2dii−Σi,j=1m(zi)(zj)wij=Σi,j=1mzi(dij−wij)zj=zT(D−W)z=zTLzL=D−W是拉普拉斯矩阵
- 为了保持尺度不变性,加约束minzTLz,s.t.zTLz=1min z^TLz,s.t.z^TLz=1minzTLz,s.t.zTLz=1
- d’>1
- 目标函数:minYTr(ZTLZ),S.t.ZTDZ=I,ZTDI=0解为:Lz=λDz,z是特征向量,归一化可得zkTDzk=1(k=1,2,...,d′)min_YTr(Z^TLZ) ,S.t.Z^TD^Z=I,Z^TD^I=0\\解为:Lz=\lambda Dz,z是特征向量,归一化可得z_k^TDz_k=1(k=1,2,...,d')minYTr(ZTLZ),S.t.ZTDZ=I,ZTDI=0解为:Lz=λDz,z是特征向量,归一化可得zkTDzk=1(k=1,2,...,d′)
- 一维z
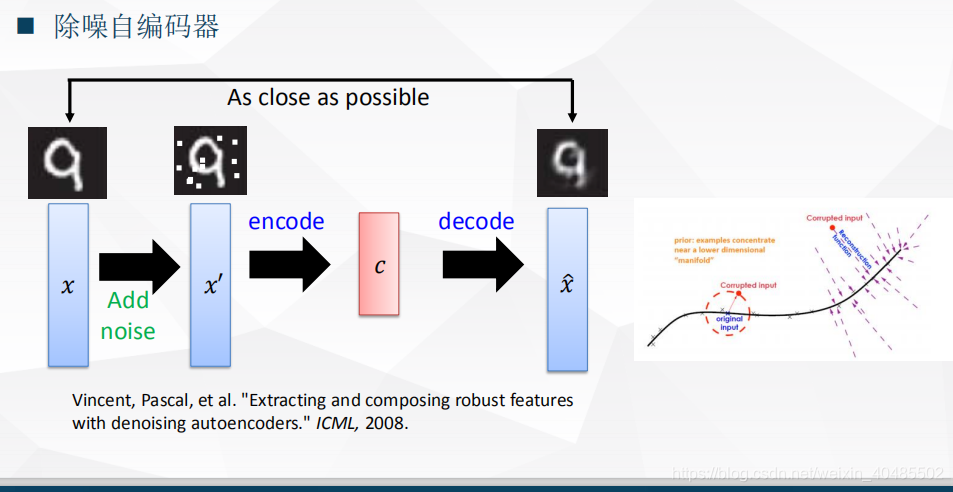
3.3.4 自编码器
- 损失函数:minw∈Rd∗d′Σi=1m∥xi−WTWxi∥2min_{w\in R^{d*d'}}\Sigma_{i=1}^m\|x_i-W^TWx_i\|^2minw∈Rd∗d′Σi=1m∥xi−WTWxi∥2–PCA(平方损失—)
- 深度自编码器,多个隐层,非线性激活函数(sigmoid,tanh),参数不一定要求对称
- 深度非线性自编码器学习如何投影数据到一个非线性流形,而不是一个子空间
- 这是一种非线性的降维方式
- RBM:就是一个绑定参数的自编码器,一个不同点是RBM的单元是随机采样的
- RBM可以通过逐层训练得到,通过近似contrastive divergence (Hinton 2006 Science)




- RBM可以通过逐层训练得到,通过近似contrastive divergence (Hinton 2006 Science)
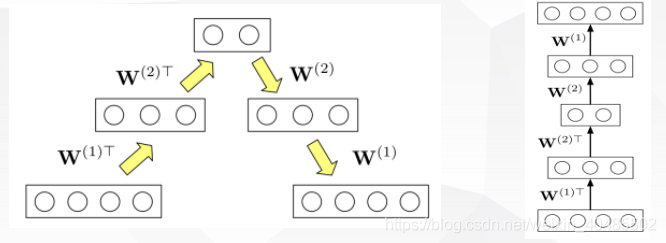
RBM-逐层训练
- 假定我们已经训练好一个RBM,其参数为W(1)
- 我们基于训练集计算隐含特征,并把隐含特征输入到另一个RBM
- 注意此时W(1)固定,W(2)使用contrastive divergence进行训练
- 两个堆叠的RBM可以被看作一个含有三个隐含层的自编码器
- 这给了深度自编码器一个好的初始化,我们可以进一步通过反向传播调优(finetune)自编码器的权重
- 这种训练策略被称为逐层预训练(layerwise pre-training)

3.3.5 word2vec
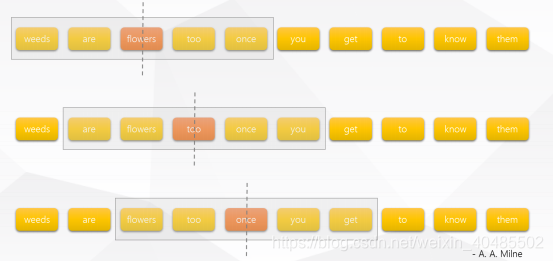
- Word2Vec:利用简单(浅层)的神经网络模型从海量的文档中学习词向量
- 利用一个窗口中上下文单词预测中间的词
- 两种模型结构:
- Skip-gram
- CBOW
- 如何计算
- 初始化:为每一个单词随机生成(固定维度的)表达
- 更新:扫描文档集合,为每一个单词重新计算其表达
- 重复2,直至收敛
- 优化难点,如何计算softmaxsoftmax(xi)=exp(xi)Σj=1nexp(xj)softmax(x_i)=\frac{exp(x_i)}{\Sigma_{j=1}^nexp(x_j)}softmax(xi)=Σj=1nexp(xj)exp(xi)
- 层次化softmax
- 不需要 V 个输出节点,只需要𝑙𝑜𝑔2 V
- 使用二叉树结构去表示输出层,每个叶子节点是一个词
- 负采样
- 选择k个负例,最大化真实出现的词的概率,最小化随机采样出来的词的概率
J(θ)=−1TΣt=1TJt(θ)Jt(θ)=logσ(uoTvc)+Σi=1Ej−P(w)[logσ(−ujTvc)]σ(x)=11+e−xJ(\theta)=-\frac{1}{T}\Sigma_{t=1}^TJ_t(\theta)\\J_t(\theta)=log \sigma(u_o^Tv_c)+\Sigma_{i=1}E_{j-P(w)}[log \sigma(-u_j^Tv_c)]\\\sigma(x)=\frac{1}{1+e^{-x}}J(θ)=−T1Σt=1TJt(θ)Jt(θ)=logσ(uoTvc)+Σi=1Ej−P(w)[logσ(−ujTvc)]σ(x)=1+e−x1
- 选择k个负例,最大化真实出现的词的概率,最小化随机采样出来的词的概率
- 层次化softmax
- Skip-gram
- 给定wt预测上下文wt+j
- 极大似然估计
- Lskip−gram=1TΣt=1TΣ−c≤j≤c.j≠ologp(wt+j∣wt)p(wt+j∣wt)=exp((Woutwt+j)T(WINwt))Σv=1Vexp((Woutwv)T(WINwt))L_{skip-gram}=\frac{1}{T}\Sigma_{t=1}^T\Sigma_{-c\leq j \leq c.j\neq o}log p(w_{t+j}|w_t)\\p(w_{t+j}|w_t)=\frac{exp((W_{out}w_{t+j})^T(W_{IN}w_t))}{\Sigma_{v=1}^Vexp((W_{out}w_{v})^T(W_{IN}w_t))}Lskip−gram=T1Σt=1TΣ−c≤j≤c.j=ologp(wt+j∣wt)p(wt+j∣wt)=Σv=1Vexp((Woutwv)T(WINwt))exp((Woutwt+j)T(WINwt))


- softmax





)
)


)










)